บทที่3
สถิติอ้างอิง
สถิติอ้างอิง ( Inferential statistics ) หมายถึง
สถิติที่ใชัในการสรุปอ้างอิงข้อมูลที่ได้จากกลุ่มตัวอย่างไปยังข้อมูลของประชากร
โดยใช้ทฤษฎีความน่าจะเป็น การประมาณค่าพารามิเตอร์ การทดสอบสมมุติฐาน ดังนั้น
เนื้อหาที่สำคัญในบทนี้จะนำเสนอในเรื่องที่เกี่ยวข้องกับสถิติอ้างอิงก่อนได้แก่
มโนทัศน์เบื้องต้นของการแจกแจงความน่าจะเป็นแบบต่างๆ Sampling
Distribution ของสถิติทดสอบแบบต่างๆ การสุ่มตัวอย่างและขนาดของกลุ่มตัวอย่าง
การประมาณค่าพารามิเตอร์ แล้วจึงนำเสนอสถิติอ้างอิงเบื้องต้นที่สำคัญ ได้แก่ การทดสอบสมมติฐาน
การวิเคราะห์ความแปร ปรวน
ส่วนความสัมพันธ์ระหว่างตัวแปรและการทำนายตัวแปร จะกล่าวในบทต่อไป
มโนทัศน์เบื้องต้นของการแจกแจงความน่าจะเป็นแบบต่างๆ
ตัวแปรสุ่ม หมายถึง
สิ่งที่มีความผันแปรโดยมีโอกาสในการเกิดความผันแปรได้เท่าๆกัน
หรือเป็นเซ็ตของค่าที่ผันแปรได้ เช่น ถ้าให้ X
เป็นตัวแปรสุ่มของการทอดลูกเต๋า 1 ครั้ง ค่าของ X ที่อาจจะเกิดขึ้นได้
มีค่าตั้งแต่ 1 – 6 โดยมีค่าความน่าจะเป็นหรือโอกาสในการเกิดค่าต่างๆได้เท่ากัน
คือ 1/6 ประเภทของตัวแปรสุ่มแบ่งได้
2 ชนิด คือ
ตัวแปรสุ่มแบบไม่ต่อเนื่อง ( Discrete random variable) และ ตัวแปรสุ่มแบบต่อเนื่อง ( Continuous random variable)
1.
ตัวแปรสุ่มแบบไม่ต่อเนื่อง ( Discrete random variable) ค่าของตัวแปรสุ่มแบบไม่ต่อเนื่อง จะมีได้เพียงบางค่าและเป็นจำนวนนับ
ซึ่งอาจมีจำนวนที่จำกัด หรือเป็นค่าอนันต์ที่นับได้ เช่น การจับใบดำ-แดงในการเกณฑ์ทหาร การโยนเหรียญ การทอดลูกเต๋า การตรวจสอบคุณภาพของสินค้า
ตัวอย่างค่าที่ได้จากการสุ่มสินค้าที่เสีย X = 0 , 1 , 2 , 3 , 4 , 5 , 6 ,
7 , 8 , 9 , 10
2. ตัวแปรสุ่มแบบต่อเนื่อง ( Continuous random variable) ค่าของตัวแปรสุ่มแบบต่อ
เนื่อง จะมีค่าจริงในช่วงที่ต่อเนื่องกัน เช่น น้ำหนัก ส่วนสูง ระยะเวลา
ตัวอย่างค่าของน้ำหนักของนักเรียนมัธยมศึกษา จะอยู่ในช่วง 40-90 กิโลกรัม เขียนได้ว่า 40 <
X < 90 กิโลกรัม
การแจกแจงความน่าจะเป็นของตัวแปรแบบไม่ต่อเนื่อง( Discrete probability distribution)
กรณีที่ตัวแปรสุ่มเป็นตัวแปรแบบไม่ต่อเนื่อง
ตัวแปรชนิดนี้จะมีค่าบางค่าและจะมีการแจกแจงความน่าจะเป็นแบบต่างๆกันขึ้นอยู่กับลักษณะของการทดลองสุ่ม
ซึ่งการแจกแจงความน่าจะเป็นของตัวแปรแบบไม่ต่อเนื่องที่ควรทราบ มีดังนี้
1. การแจกแจงแบบทวินาม (
Binomial distribution)
เป็นการแจกแจงของตัวแปรสุ่มที่ไม่ต่อเนื่อง(Discrete random variable) ที่ในการทดลองแต่ละครั้งจะเกิดผลลัพธ์เพียง
2 อย่าง คือ สำเร็จ (success)กับผิดหวัง(failure)
การแจกแจงแบบทวินาม เขียนแทนด้วย b( x, n, p )
โดยที่ n คือ การทดลองซ้ำๆกันในสภาวะเหมือนๆกัน อย่างเป็นอิสระ
x คือ
จำนวนความสำเร็จที่ได้จากการทดลอง n ครั้ง
p คือ ความน่าจะเป็นที่พบความสำเร็จ
ตัวอย่างเหตุการณ์ที่มีการแจกแจงแบบทวินาม เช่น การโยนเหรียญ การมีบุตร การทำข้อสอบเลือกตอบ ดังแสดงในตาราง 3.1
ตาราง 3.1
ตัวอย่างของตัวแปรทวินาม
|
การทดลอง |
สำเร็จ |
ไม่สำเร็จ |
p |
n |
x |
|
การโยนเหรียญ |
หัว |
ก้อย |
1/2 |
จำนวนครั้งในการโยนเหรียญ |
จำนวนครั้งที่ออกหัว |
|
การมีบุตร |
หญิง |
ชาย |
1/2 |
จำนวนบุตร |
จำนวนบุตรสาวในครอบครัว |
|
การทำข้อสอบเลือกตอบ 4 ตัวเลือก |
ถูก |
ผิด |
1/4 |
จำนวนข้อสอบ |
จำนวนข้อที่ตอบถูก |
การคำนวณค่าการแจกแจงความน่าจะเป็นแบบทวินาม
สมมติการสอบครั้งหนึ่ง เหลือเวลาอีก 3 วินาที
แต่ยังมีข้อสอบ 4 ตัวเลือกอีก 3
ข้อที่ยังไม่ได้ทำ นิสิตจึงตัดสินใจทำข้อสอบทั้ง 3
ข้อโดยไม่อ่าน จงหาความน่าจะเป็นในการทำข้อสอบได้ถูกทั้ง 3
ข้อ ถูกเพียง 2 ข้อ ถูกเพียง 1 ข้อ และไม่ถูกเลย
ความน่าจะเป็นในการทำข้อสอบถูกในแต่ละข้อ = .25
ความน่าจะเป็นในการทำข้อสอบผิดในแต่ละข้อ = .75 (ข้อสอบมี 4 ตัวเลือก)
ความน่าจะเป็นที่จะทำข้อสอบถูก 3 ข้อ 2 ข้อ 1ข้อ 0 ข้อ สามารถหาได้
ดังนี้
p
(ถูก 3 ข้อ) = p(TTT)
= p3
=
.25 3
=
.02
p
(ถูก 2 ข้อ) = p(TTF) หรือ ( TFT) หรือ(FTT)
= p(TTF) + p( TFT) + p(FTT)
= (.25´.25´.75) + (.25´.25´.75) +(.25´.25´.75)
= .046+.046+.046 = .14
p
(ถูก 1 ข้อ) = p(TFF) หรือ (
FTF) หรือ(FFT)
= p(TFF) + p(
FTF) + p(FFT)
= (.25´.75´.75) + (.75´.25´.75) +(.75´.75´.25)
= .14+.14+.14 = .42
p
(ถูก 0 ข้อ) = p(FFF)
= p3
=
.75 3
=
.42
เพื่อความสะดวกนักคณิตศาสตร์สถิติได้คิดสูตรสำเร็จเพื่อหาความน่าจะเป็นแบบทวินาม
ดังนี้
สูตรที่ใช้หาค่าความน่าจะเป็นที่จะเกิดความสำเร็จ
b(
x, n, p ) = n Cx px q n – x
= n ! px
q n – x
![]() x ! (n – x ) !
x ! (n – x ) !
โดยที่ n = จำนวนครั้งในการทดลอง
x = ความสำเร็จที่เกิดขึ้น
p = ความน่าจะเป็นที่จะพบความสำเร็จ
q = ความน่าจะเป็นที่จะพบความผิดหวัง
ตัวอย่าง
จากข้อมูลการส่งแบบสอบถามไปยังสถาบันการศึกษาทั่วประเทศ
พบว่าจะได้รับกลับคืนมา 60%
ถ้าสุ่มเลือกสถาบันการศึกษา 3 แห่ง แล้วส่งแบบสอบถามไปให้
จงหาความน่าจะเป็นที่จะได้รับแบบสอบถามกลับคืนมา
กรณีที่ 1 3 ฉบับ
กรณีที่ 2 2 ฉบับ
กรณีที่ 3
น้อยกว่า 2 ฉบับ
การแจกแจงแบบทวินาม เขียนแทนด้วย b( x, n, p )โดยที่
กรณีที่ 1 x = 3 n = 3 p = 0.60
b( x, n, p
) = n
Cx px q
n – x
![]() =
n ! px q n – x
=
n ! px q n – x
x ! (n – x ) !
=
3 ! 0.63 0.4 0
= 0.22
![]() 3 ! (3 – 3 ) !
3 ! (3 – 3 ) !
กรณีที่ 2 x = 2 n = 3 p = 0.60
b( x, n, p
)![]() =
n ! px q n – x
=
n ! px q n – x
x ! (n – x ) !
=
3 ! 0.62 0.4 1
= 3´ 0.14 = 0.42
![]() 2 ! (3 – 2 ) !
2 ! (3 – 2 ) !
กรณีที่ 3 x = 1และ 0 n = 3 p = 0.60
b( x, n, p
)![]() =
n ! px q n – x
=
n ! px q n – x
x ! (n – x ) !
=
3 ! 0.61 0.4 2
= 3´0.096 = 0.29
![]() 1 ! (3 – 1 ) !
1 ! (3 – 1 ) !
และ b( x, n, p )=
3 ! 0.60 0.4 3
= 0.06
![]() 0 ! (3 –0) !
0 ! (3 –0) !
=
0.29+.06
= 0.35
นอกจากการคำนวณความน่าจะเป็นแบบทวินามแล้ว
นักสถิติได้สร้างตารางการแจกแจงความน่าจะเป็นทวินาม
เมื่อต้องการหาความน่าจะเป็นแบบทวินามจากตารางจะต้องทราบค่า
n , p , x โดยใช้ตาราง ความน่าจะเป็นแบบทวินาม
ในภาคผนวก
ค่าเฉลี่ยและความแปรปรวนแบบทวินาม
E(x)
= S x. p(x) = np
Var (x) = E( X
- m )2
= npq
ตัวอย่าง ในระยะ 5
ปีที่ผ่านมา สำนักทะเบียนพบว่าในแต่ละปีที่นิสิตลงทะเบียนเรียนวิชาเลือกเสรี ก.เมื่อต้นเทอม จะมีการถอนวิชานี้ถึง 20%
ถ้าปีนี้มีนิสิตลงทะเบียนวิชานี้ 100 คน
โดยเฉลี่ยจะมีนิสิตเรียนจบวิชานี้กี่คนและมีความแปรปรวนเท่ากับเท่าไร
การตัดสินใจของนิสิตคนหนึ่งก็คือการทดลอง1 ครั้ง
นิสิต 100 คน ก็มีการทดลอง 100 ครั้ง
n
= 100
การตัดสินใจที่เกิดขึ้น คือ ถอน กับไม่ถอน
ความน่าจะเป็นที่จะเกิดขึ้นในการถอน(q) =
.20
ความน่าจะเป็นที่จะเรียนจบวิชานี้ (p)=
.80
โดยเฉลี่ยแล้วจะมีนิสิตเรียนจบวิชานี้ ใช้สูตร
E(x)
= S x. p(x) = np
= 100´0.80
=
80
คน
โดยมีความแปรปรวน
= npq
= 100 ´ 0.80 ´ 0.20
= 16
ตัวอย่าง บารมีเป็นนักกีฬาของสถาบัน
ความน่าจะเป็นที่บารมีจะชู๊ตลูกบอลลงตาข่าย คือ0.5 ในการแข่งขันครั้งนี้ บารมีมีโอกาสชู๊ตลูกบอล 6 ครั้ง อยากทราบว่าบารมีน่าจะชู๊ตลูกบอลลงห่วงกี่ครั้ง และค่าส่วนเบี่ยงเบนมาตรฐานเท่ากับเท่าไร
จากโจทย์ n = 6
p = 0.5
q = 1 - 0.5 = 0.5
E(x)
=
np
=
6 ´ 0.5 = 3
บารมีน่าจะชู๊ตลูกบอลลงห่วง = 3 ครั้ง
Var (x) =
E( X - m )2 =
npq
= 6 ´ 0.5´ 0.5 = 1.5
ส่วนเบี่ยงเบนมาตรฐาน
= 1.22
2. การแจกแจงความน่าจะเป็นแบบปัวซอง
(Poisson distribution)
![]()
![]() การแจกแจงชนิดนี้มีประโยชน์มากช่วยแก้ไขขีดจำกัดของการแจกแจงความน่าจะเป็นแบบทวินาม
เมื่อความน่าจะเป็นที่จะพบความสำเร็จมีค่าน้อยมาก ( p 0 ) และจำนวนการทดลอง n มีค่ามาก ( n ¥) การแจกแจงแบบนี้ยังมีประโยชน์ใช้กับจำนวนความสำเร็จหรือเหตุการณ์ที่สนใจเกิดขึ้นในช่วงเวลาใดเวลาหนึ่ง
เช่น จำนวนผู้ป่วยที่มาโรงพยาบาลในช่วงเวลา 9.00-10.00 น.
จำนวนรถหายในเดือนมกราคม
จำนวนคำที่พิมพ์ผิดต่อหน้า เป็นต้น
การแจกแจงชนิดนี้มีประโยชน์มากช่วยแก้ไขขีดจำกัดของการแจกแจงความน่าจะเป็นแบบทวินาม
เมื่อความน่าจะเป็นที่จะพบความสำเร็จมีค่าน้อยมาก ( p 0 ) และจำนวนการทดลอง n มีค่ามาก ( n ¥) การแจกแจงแบบนี้ยังมีประโยชน์ใช้กับจำนวนความสำเร็จหรือเหตุการณ์ที่สนใจเกิดขึ้นในช่วงเวลาใดเวลาหนึ่ง
เช่น จำนวนผู้ป่วยที่มาโรงพยาบาลในช่วงเวลา 9.00-10.00 น.
จำนวนรถหายในเดือนมกราคม
จำนวนคำที่พิมพ์ผิดต่อหน้า เป็นต้น
การแจกแจงความน่าจะเป็นแบบปัวซองนี้จะเกี่ยวข้องกับการทดลองแบบปัวซองที่มีคุณสมบัติ
ดังนี้
1) จำนวนความสำเร็จที่เกิดขึ้นในช่วงเวลาใดเวลาหนึ่ง
หรือในสถานการณ์ใดสถานการณ์
หนึ่งเป็นอิสระจากความสำเร็จที่เกิดขึ้นในช่วงเวลาอื่นๆหรือสถานการณ์อื่นๆ
2) ![]()
![]() ความน่าจะเป็นที่จะพบความสำเร็จมีค่าน้อยมาก p
0 , q
1 และความน่าจะเป็นนี้จะเป็นปฏิภาคกับเวลา
ความน่าจะเป็นที่จะพบความสำเร็จมีค่าน้อยมาก p
0 , q
1 และความน่าจะเป็นนี้จะเป็นปฏิภาคกับเวลา
ถ้า x คือจำนวนความสำเร็จที่ได้จากการทดลองแบบปัวซอง และเป็นตัวแปรสุ่มแบบปัวซอง
ดังนั้น การแจกแจงความน่าจะเป็นแบบปัวซองก็คือ
การแจกแจงความน่าจะเป็นของตัวแปรสุ่มปัวซองที่เป็นจำนวนความสำเร็จที่เกิดขึ้นในช่วงเวลาใดเวลาหนึ่ง
หรือในสถานการณ์ใดสถานการณ์หนึ่ง การแจกแจงนี้เขียนได้ด้วยสัญลักษณ์ p( x ,
l) แสดงว่าการแจกแจงขึ้นอยู่กับ
l โดยที่ lคือค่าเฉลี่ยของความสำเร็จที่เกิดขึ้นในช่วงเวลาหนึ่ง
หรือสถานการณ์หนึ่ง
ความน่าจะเป็นที่จะพบความสำเร็จ x ครั้ง ในช่วงเวลาหนึ่งหรือสถานการณ์หนึ่งคือ
![]() p( x , l)
= e -l l x
เมื่อ x คือ 0,1,2,…
p( x , l)
= e -l l x
เมื่อ x คือ 0,1,2,…
x!
l
= ค่าเฉลี่ยของความสำเร็จที่เกิดขึ้น
e
= 2.71828
ดังนั้นการคำนวณหาความน่าจะเป็นโดยใช้การแจกแจงแบบปัวซองจะต้องทราบค่าเฉลี่ยของตัวแปรสุ่มแบบปัวซองก่อนเสมอ
![]()
![]() เนื่องจาก
p
0 , q
1 ดังนั้น m
= np = l และ s2 = npq = l
เนื่องจาก
p
0 , q
1 ดังนั้น m
= np = l และ s2 = npq = l
ตัวอย่าง
ถ้าสถิติคนตายด้วยอุบัติเหตุของเมืองหนึ่งโดยเฉลี่ย วันละ 6.5 คน และเมืองนี้มีประชากร 237,000 คน จงหาความน่าจะเป็นที่
1) มีคนตาย 5 คน
2) ไม่มีคนตายเลย
l = 6.5
![]() 1)
p( x , l)
=
e -l l x
1)
p( x , l)
=
e -l l x
x!
p( 5 , 6.5) = (2.71828) – 6. 5 6.5 5
![]() 5!
5!
ความน่าจะเป็นที่จะมีคนตาย 5 คน = 0.1450
2)
p( x , l)
=
e -l l x
![]() x!
x!
p( 0 , 6.5) = (2.71828) – 6. 5 6.5 0
![]() 0!
0!
ความน่าจะเป็นที่จะไม่มีคนตาย = 0.0015
เพื่อความสะดวกและรวดเร็ว
นักคณิตศาสตร์จึงได้สร้างตารางของการแจกแจงความ
น่าจะเป็นของการแจกแจงแบบปัวซอง โดยจะต้องทราบค่า x และ l
โดยเปิดตารางความน่าจะเป็นแบบปัวซอง
ในภาคผนวก
การแจกแจงของตัวแปรสุ่มที่ต่อเนื่อง (Continuous
random variable)
การแจกแจงของตัวแปรสุ่มที่ต่อเนื่องที่สำคัญที่จะกล่าวถึงในตอนนี้ ได้แก่
การแจกแจงแบบโค้งปกติ
การแจกแจงปกติมาตรฐาน
การแจกแจงแบบที
การแจกแจงแบบไคสแควร์ และ
การแจกแจงแบบเอฟ
ตัวแปรสุ่มแบบต่อเนื่อง ( Continuous random variable) ค่าของตัวแปรสุ่มแบบต่อเนื่อง
จะมีค่าจริงในช่วงที่ต่อเนื่องกัน เช่น
น้ำหนัก ส่วนสูง ระยะเวลา
ตัวอย่างค่าของน้ำหนักของนักเรียนมัธยมศึกษา จะอยู่ในช่วง 40-90 กิโลกรัม เขียนได้ว่า 40 < X < 90 กิโลกรัม
Sample
space ของตัวแปรสุ่มแบบต่อเนื่องจะประกอบด้วยปริมาณต่าง ๆ
ซึ่งเป็นค่าที่ได้จากการวัด เช่น ค่าความเร็วของรถที่วัดได้
ค่าน้ำหนักของสัตว์ที่วัดได้ในห้องทดลอง ค่าความสูงของนักเรียนที่วัดได้… ค่าต่าง ๆ เหล่านี้ที่วัดได้มีได้มากมายนับไม่ถ้วนจนเราไม่สามารถหาค่าความน่าจะเป็นที่จะเกิดค่าใดค่าหนึ่งได้
ต้องหาเป็นช่วงหรือเป็นพื้นที่ เช่น เราจะหาค่าความน่าจะเป็นที่รถจะวิ่งไปที่ใด ๆ
ด้วยความเร็ว 60 ถึง 70 กม./ ชั่วโมง หาค่าความน่าจะเป็นที่สัตว์ในห้องทดลองจะหนัก 6.5 ถึง 8.5 ออนซ์
เป็นต้น
![]()
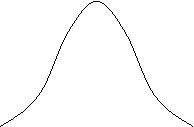 ค่าความน่าจะเป็นที่สัมพันธ์กับตัวแปรสุ่มแบบไม่ต่อเนื่องถูกกำหนดโดยแท่งสี่เหลี่ยมผืนผ้า
กล่าวคือสร้างเป็นรูปฮิสโทแกรมได้ ในกรณีของตัวแปรสุ่มแบบต่อเนื่อง
จะแทนความน่าจะเป็นโดยใช้พื้นที่เช่นกัน ดังแสดงในรูป 1
แต่แทนที่จะแทนด้วยแท่งสี่เหลี่ยมผืนผ้าก็จะแทนด้วยพื้นที่ใต้โค้ง
ค่าความน่าจะเป็นที่สัมพันธ์กับตัวแปรสุ่มแบบไม่ต่อเนื่องถูกกำหนดโดยแท่งสี่เหลี่ยมผืนผ้า
กล่าวคือสร้างเป็นรูปฮิสโทแกรมได้ ในกรณีของตัวแปรสุ่มแบบต่อเนื่อง
จะแทนความน่าจะเป็นโดยใช้พื้นที่เช่นกัน ดังแสดงในรูป 1
แต่แทนที่จะแทนด้วยแท่งสี่เหลี่ยมผืนผ้าก็จะแทนด้วยพื้นที่ใต้โค้ง
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
รูป1
รูป
1
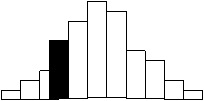
ทางซ้ายแทนการแจกแจงความน่าจะเป็นของตัวแปรสุ่มซึ่งมีค่า 0, 1, 2, …, 10 และความน่าจะเป็นที่จะได้ค่า 3
แสดงด้วยพื้นที่ส่วนที่แรเงา
รูป 1 ทางขวาแสดงค่าของตัวแปรสุ่มแบบต่อเนื่องซึ่งจะเป็นค่าใดก็ได้บนช่วง 0-10 ความน่าจะเป็นที่จะได้ค่าระหว่าง 3.0 กับ 4.0 แสดงด้วยพื้นที่ใต้โค้งที่แรเงาด้วยสีทึบซึ่งอยู่ทางซ้ายของรูป และความน่าจะเป็นที่จะได้ค่า
8
ขึ้นไปแสดงด้วยพื้นที่ใต้โค้งที่แรเงาด้วยสีทึบซึ่งอยู่ทางขวาของรูป
รูปโค้งที่แสดงทางขวาของรูป 1
ก็คือกราฟของฟังก์ชันที่มีชื่อเฉพาะว่า Probability density function
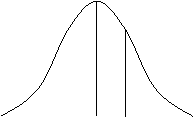
พื้นที่ใต้โค้งระหว่าง 2 ค่าใด ๆ a และ b (ดังรูป 2) ใช้บอกค่าความน่าจะเป็นของตัวแปรสุ่มแบบต่อเนื่องเป็นช่วงจาก
a ถึง b
![]()
![]()
a b
รูป 2
ค่าของ Probability density function จะไม่มีทางเป็นลบ
และพื้นที่ใต้โค้งทั้งหมดมีค่าเท่ากับ 1 เสมอ
1. การแจกแจงแบบโค้งปกติ
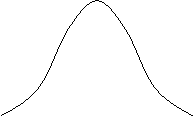
![]() การแจกแจงความน่าจะเป็นของตัวแปรสุ่มแบบต่อเนื่องที่สำคัญที่สุดคือการแจกแจงปกติ
(Normal distribution) กราฟของการแจกแจงปกติเรียกว่า
โค้งปกติ (Normal curve) ซึ่งมีลักษณะเหมือนระฆังคว่ำ ดังรูป
3
การแจกแจงความน่าจะเป็นของตัวแปรสุ่มแบบต่อเนื่องที่สำคัญที่สุดคือการแจกแจงปกติ
(Normal distribution) กราฟของการแจกแจงปกติเรียกว่า
โค้งปกติ (Normal curve) ซึ่งมีลักษณะเหมือนระฆังคว่ำ ดังรูป
3
![]()
m
รูป 3 โค้งปกติ
ข้อมูลส่วนใหญ่มักจะมีการแจกแจงเป็นรูปโค้งปกติ ใน ค.ศ. 1733 De Moivre เป็นผู้สร้างสมการทางคณิตศาสตร์ของโค้งปกติขึ้น
การแจกแจงปกตินี้ บางทีเรียกว่า Gaussian distribution เพื่อเป็นเกียรติกับ
Karl Gauss (ค.ศ. 1777 – 1855) ผู้ซึ่งได้สร้างสมการสำหรับโค้งปกติจากการศึกษาความคลาดเคลื่อนที่เกิดขึ้นเมื่อมีการวัดซ้ำ
ๆ กัน
ตัวแปรสุ่ม X ที่มีการแจกแจงเป็นรูประฆังคว่ำดังแสดงในรูป
3 เรียกว่า “ตัวแปรสุ่มปกติ”
(Normal random variable) สมการทางคณิตศาสตร์สำหรับการแจกแจงความน่าจะเป็นของตัวแปรสุ่มแบบต่อเนื่อง
ขึ้นอยู่กับค่าพารามิเตอร์ 2 ตัว คือ m (Mean) และ s (Standard deviation) ดังนั้น Probability
density function ของตัวแปรสุ่ม X จึงแสดงด้วย
n (X ; m, s)
โค้งปกติ
ถ้า X เป็นตัวแปรสุ่มปกติด้วยค่าเฉลี่ย = m และความแปรปรวน = s2 แล้ว
สมการของโค้งปกติคือ (Walpole, 1974 : 102)

เมื่อ p = 3.14159… และ e = 2.71828…
หรือเขียนในอีกรูปหนึ่งคือ
![]()
เมื่อ Y เป็นส่วนสูงของโค้ง (Ordinate) ขึ้นอยู่กับค่า X
แต่ละค่า
p เป็นตัวคงที่มีค่า 3.1416
e เป็นตัวคงที่อีกตัวหนึ่งมีค่า 2.7183
จากสมการโค้งปกติแสดงว่า โค้งปกติไม่ใช่มีเพียงรูปเดียว แต่มีได้หลาย ๆ
รูป โดยจะมีรูปร่างโด่งมาก (Leptokertic) โด่งปานกลาง (Mesokertic)
หรือที่รู้จักกันทั่วไปว่าโค้งปกติ (Normal curve) หรือโค้งลาด (platykertic) แตกต่างกันออกไปขึ้นอยู่กับค่า
m และ s นั่นคือโค้งจะอยู่ตรงตำแหน่งใดของแกนนอนขึ้นอยู่กับค่า
m และลักษณะของโค้งจะโด่งมากน้อยเพียงใดหรือลาดเพียงใดขึ้นอยู่กับค่าของ
s ถ้า s มากโค้งจะลาด ถ้า s น้อยโค้งจะโด่ง ดังแสดงได้ด้วยรูปต่าง ๆ
ดังนี้
![]()
![]()
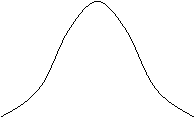
 s1 s2
s1 s2
![]()
m1
m2 X
รูป 4 รูปโค้งปกติเมื่อ
m1
¹
m2
s1
=
s2
![]()
 s1
s1
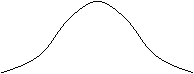
s2
![]()
m1
= m2 X
รูป 5 รูปโค้งปกติเมื่อ m1
=
m2
s1
< s2
s1
![]()
![]()
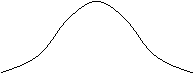
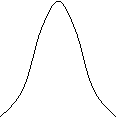
![]() m1 m2 X
m1 m2 X
รูป 6 รูปโค้งปกติเมื่อ m1
¹
m2
s1
< s2
รูป 4 เป็นรูปโค้งปกติ 2
รูปที่มีความเบี่ยงเบนมาตรฐานเท่ากัน แต่ค่าเฉลี่ยไม่เท่ากัน รูปโค้งปกติ 2 รูปนี้มีรูปร่างเหมือนกัน แต่อยู่คนละตำแหน่งกันเพราะค่าเฉลี่ยไม่เท่ากัน
นั่นคือ ถ้ามี s เท่ากัน แต่ m ไม่เท่ากัน จะเป็นโค้งคนละรูป
รูป 5 เป็นรูปโค้งปกติ 2
รูปที่มีค่าเฉลี่ยเท่ากันแต่ความเบี่ยงเบนมาตรฐานไม่เท่ากัน โค้งปกติ 2 รูปนี้มีจุดกึ่งกลางอยู่ที่ตำแหน่งเดียวกันบนแกน X แต่โค้งปกติที่มีค่าความเบี่ยงเบนมาตรฐานสูงจะต่ำกว่าและแผ่กว้างกว่า
นั่นคือ ถ้ามี m เท่ากัน แต่ s ไม่เท่ากัน จะเป็นโค้งคนละรูป
โปรดจำไว้ว่าพื้นที่ใต้โค้งปกติจะต้องเท่ากับ 1 เสมอ
ดังนั้นถ้าค่าสังเกตยิ่งแตกต่างกันมาก โค้งก็จะยิ่งต่ำและลาด
รูป 6 แสดงรูปโค้งปกติ 2 รูป
ที่มีค่าเฉลี่ยไม่เท่ากันและความเบี่ยงเบนมาตรฐานไม่เท่ากัน รูปโค้งปกติทั้ง 2 รูปมีจุดกึ่งกลางอยู่ตำแหน่งต่างกันบนแกน X และมีรูปร่างต่างกันด้วย
นั่นคือ ถ้า m และ s ไม่เท่ากัน โค้งจะเป็นคนละรูป
ตัวอย่างการแจกแจงปกติ 3 รูปที่มีค่า m และ s ต่างกัน
f(X)
s = 1
m =
40
X
f(X)

![]()
![]() s = 5
s = 5
m
= 10
X
 f(X)
f(X)
![]() s
= 2
s
= 2
m
= 50
X
สมการของโค้งปกติขึ้นอยู่กับค่าของ m และ s จึงทำให้ได้โค้งปกติรูปร่างต่าง
ๆ กันไปดังแสดงในรูป 4, 5, 6
ซึ่งทำให้พื้นที่ใต้โค้งมีค่าต่าง ๆ ไปด้วย
ในทางปฏิบัติจะหาพื้นที่ใต้โค้งโดยใช้ตารางสำเร็จในภาคผนวก
เนื่องจากว่าเป็นไปไม่ได้และไม่จำเป็นด้วยที่จะสร้างตารางหาพื้นที่ใต้โค้งสำหรับ
m และ s ที่เกิดขึ้นทุกคู่
จึงได้มีการสร้างตารางแสดงพื้นที่สำหรับการแจกแจงปกติที่มี m = 0, s = 1 เท่านั้น ซึ่งมีชื่อเรียกเฉพาะว่า Standard
normal distribution สำหรับใช้กับโค้งปกติรูปต่าง ๆ
แล้วหาพื้นที่ใต้โค้งปกติใด ๆ ได้ โดยเปลี่ยนค่าของสเกลเดิมหรือ X-scale (ดังรูป 7) เป็นหน่วยมาตรฐาน (Standard units)
หรือคะแนนมาตรฐาน (Standard scores) หรือคะแนนซี
(Z-scores) โดยใช้สูตร
![]()
Z-score
นี้เป็นสเกลใหม่ ซึ่งค่า Z จะบอกให้ทราบว่ามีอยู่กี่ความเบี่ยงเบนมาตรฐานที่อยู่เหนือหรือใต้ค่าตัวกลางเลขคณิต
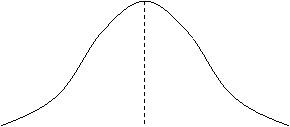
![]()
m-3s m-2s m-s m m+s m+2s m+3s
X-Scale
![]() -3
-2
-1
0
1 2
3
Z-Scale
-3
-2
-1
0
1 2
3
Z-Scale
รูป 7
คุณสมบัติที่สำคัญของโค้งปกติ (Walpole.
1974 : 103)
1. ค่าของฐานนิยมอยู่ที่ X
= m ซึ่งเป็นจุดบนแกน X ที่เกิดจากการลากเส้นตั้งฉากจากจุดที่โค้งสูงที่สุดลงมายังแกนนอน
X
2. โค้งมีลักษณะสมมาตร
ถ้าแบ่งโค้งนี้ตามเส้นแนวตั้งตรงค่าของ m เส้นแนวตั้งนี้จะแบ่งพื้นที่ออกเป็น
2 ส่วนเท่า ๆ กัน
3. เส้นโค้งจะเข้าใกล้แกนนอน
X ไปเรื่อย ๆ ทั้ง 2 ข้าง
แต่ไม่จรดแกนนอน
4. พื้นที่ใต้โค้งทั้งหมดมีค่าเท่ากับ
1
5. พื้นที่ใต้โค้งเกือบทั้งหมดอยู่ระหว่าง
m - 3s และ m + 3s
การหาพื้นที่ใต้โค้งปกติ
พื้นที่ใต้โค้งปกติทั้งหมดมีค่าเป็น 1
หรืออาจจะทำเป็นเปอร์เซ็นต์ก็ได้ โดยคูณด้วย 100
ในการหาพื้นที่ใต้โค้งจะต้องหาคะแนนมาตรฐานซี
(Z-score) ก่อน จากสูตร
![]()
เมื่อ Z แทนค่าของคะแนนมาตรฐานซี
X แทนค่าของคะแนนดิบใด ๆ ที่ต้องการแปลงเป็น Z
m แทนตัวกลางเลขคณิตของคะแนนชุด X
s
แทนความเบี่ยงเบนมาตรฐานของคะแนนชุด X
คุณสมบัติของคะแนนมาตรฐาน Z
1. ค่าเฉลี่ยของคะแนนมาตรฐาน (Z) = 0
2. คะแนนมาตรฐาน Z มีค่าเป็นบวกและลบ
3. ความแปรปรวนของคะแนนมาตรฐาน(s2) = 1
4. ผลบวกของคะแนนมาตรฐาน Z = 0
5. ผลบวกกำลังสองของคะแนนมาตรฐานมีค่าเท่ากับจำนวนข้อมูล SZ2 = N
6. การแจกแจงของคะแนนมาตรฐานเหมือนการแจกแจงของคะแนนดิบ
การแจกแจงของคะแนนมาตรฐานมีค่าเฉลี่ยเลขคณิต เท่ากับ 0 และส่วนเบี่ยงเบนมาตรฐานเท่า
กับ 1
จึงทำให้สามารถนำค่าคะแนนมาตรฐานมาเปรียบเทียบได้
จากสูตรจะเห็นว่า Z-score ก็คือคะแนนดิบที่ถูกแปลงให้เป็นหน่วยของความเบี่ยงเบนมาตรฐานนั่นเอง
เพื่อจะหาว่ามีอยู่กี่หน่วยความเบี่ยงเบนมาตรฐานที่คะแนนดิบอยู่เหนือหรือใต้ตัวกลางเลขคณิต
ถ้าคะแนนดิบ X อยู่เหนือตัวกลางเลขคณิตหนึ่งหน่วยความเบี่ยงเบนมาตรฐานก็จะมีค่า
Z เป็น 1 ถ้าคะแนนดิบ X อยู่ใต้ตัวกลางเลขคณิตครึ่งหน่วยความเบี่ยงเบนมาตรฐานคะแนนดิบ X ตัวนี้ก็จะมีค่า Z เป็น –0.5
เป็นต้น
ขั้นตอนในการคำนวณคะแนนมาตรฐานซี มีดังนี้
ขั้นที่ 1 หาค่าตัวกลางเลขคณิต (m) และความเบี่ยงเบนมาตรฐาน (s) ของ
คะแนนชุด X
ขั้นที่ 2 เอาคะแนนดิบ X ตั้งลบด้วย m (ต้องเอา X เป็นตัวตั้งเสมอไม่ว่า
X จะมี
ค่ามากหรือน้อยกว่า m ก็ตาม)
ขั้นที่ 3 เอา s หารค่าในขั้นที่ 2
ตัวอย่างที่ 1
จากการวัดความถนัดของนิสิตชั้นปีที่ 1
ของมหาวิทยาลัยแห่งหนึ่ง พบว่าหาตัวกลางเลขคณิต m ได้ 48
และหาความเบี่ยงเบนมาตรฐาน s ได้ 8 ถ้า X
เป็น 43 จะเท่ากับ Z เท่าใด
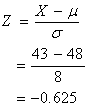
นั่นคือ คะแนนดิบ X = 43 อยู่ใต้ตัวกลางเลขคณิต 0.625 หน่วยความเบี่ยงเบนมาตรฐาน
ข้อสังเกต บางครั้งโจทย์อาจจะไม่บอกค่า m และ s แต่บอกคะแนนทั้งชุดให้ก่อนที่จะหา Z จะต้องหา m และ s ก่อน โดยใช้สูตรตามที่กล่าวมาแล้ว
จาก Z-score ที่คำนวณได้ นำไปหาพื้นที่ใต้โค้งปกติในลักษณะต่าง
ๆ ได้ โดยใช้ตารางหาพื้นที่ใต้โค้งปกติ ซึ่งอยู่ในภาคผนวก
ตัวอย่างที่ 2
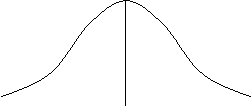
ผลการสอบวิชาสถิติของนิสิตกลุ่มหนึ่ง หาตัวกลางเลขคณิต (m) ได้ 16
และความเบี่ยงเบนมาตรฐาน (s) ได้ 5 นิสิต ก.
สอบได้ 24.65 คะแนน จงหาพื้นที่ที่อยู่ระหว่างตัวกลางเลขคณิตกับคะแนน
24.65
ในการหาพื้นที่ใต้โค้ง จำเป็นต้องใช้ Z-score เพราะฉะนั้นจะต้องแปลงคะแนนดิบ
(X) ที่กำหนดให้เป็น Z-score ก่อนโดยใช้สูตร

ที่ Z-score เท่ากับ 1.73 จากตาราง หาพื้นที่ใต้โค้งได้ 0.4582 หรือ 45.82% ซึ่งเป็นพื้นที่ระหว่างตัวกลางเลขคณิตกับคะแนนของนิสิต ก. เนื่องจากพื้นที่ใต้โค้งทั้งหมด ทางซ้ายของตัวกลางเลขคณิตมีค่า 50%
เพราะฉะนั้นสามารถสรุปได้อีกอย่างหนึ่งว่มีพื้นที่ใต้โค้งทั้งหมดอยู่
95.82% (50% + 45.82%) ที่อยู่ใต้คะแนน 24.65 ซึ่งแสดงว่านิสิต ก. อยู่ในตำแหน่งเปอร์เซ็นต์ไทล์ (Percentile
rank) ที่ 95.82 นั่นคือที่ Z = 1.73 แปลได้ว่ามีนิสิตที่ได้คะแนนต่ำกว่านิสิต ก. อยู่ 96 คนใน 100 คน
![]() .4582
.4582
![]()
0 1.73
รูป 8 แสดงการหาพื้นที่ใต้โค้งระหว่างตัวกลางเลขคณิตกับคะแนน
X
ถ้านิสิต ข. สอบได้คะแนน 7.35
แปลงเป็น Z-score ได้ดังนี้
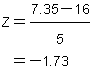
ถ้า Z ติดลบก็ใช้ ตาราง เช่นเดียวกันกับ Z เป็นบวก เพียงแต่อยู่คนละข้างกันเท่านั้น ดังนั้นพื้นที่ใต้โค้งที่อยู่ระหว่างตัวเลขคณิตกับคะแนน
7.35 จึงมีค่าเท่ากับ 45.82%
ถ้าจะหาพื้นที่ใต้โค้งที่อยู่ใต้คะแนน 7.35 ทำได้ 2 วิธีคือ วิธีหนึ่งเปิดจาก ตาราง ซึ่งจะได้พื้นที่ใต้โค้ง 0.0418 หรือ 4.18% อีกวิธีหนึ่งคือเอา 45.82% ลบออกจาก 50% จะได้ 4.18%
แสดงว่านิสิต ข. อยู่ในตำแหน่งเปอร์เซ็นต์ไทล์ที่ 4.18
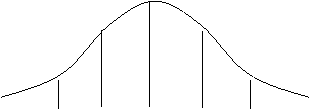
สำหรับความสัมพันธ์ระหว่าง Raw score, Z-score และ Percentile
rank ได้แสดงให้เห็นดังรูป 9 โดยให้
![]()
![]()
![]() Raw
score 20 30 40 50 60 70 80
Raw
score 20 30 40 50 60 70 80
Z-score -3 -2 -1 0 +1 +2 +3
Percentile
rank 0.13 2.28 15.87 50.00 84.13 97.72 99.87
รูป 9 ความสัมพันธ์ระหว่าง Raw score, Z-score และ Percentile
rank ของรูปที่มีการแจกแจง
โค้งปกติ ซึ่งมี m = 50 และ s = 10
เนื่องจากค่า Z-SCORE มีค่าติดลบและเป็นทศนิยม นักการศึกษาจึงนิยมแปลงคะแนนZ ให้มีScale ใหญ่ขึ้น ค่าติดลบหรือทศนิยมจะได้หมดไป
โดยแปลงให้เป็นคะแนน T โดยที่
T
= 10Z+50
จากตัวอย่างที่ 2 ถ้าต้องการหาค่า คะแนน T ของนิสิต ก. ซึ่งได้คะแนน Z =1.73 หาได้ ดังนี้
T = (10 X 1.73)+50
= 67.3
การใช้การแจกแจงปกติมาตรฐานประมาณค่าการแจกแจงแบบทวินาม
![]() เมื่อจำนวนครั้งของการทดลองทวินามมีขนาดใหญ่ ( n
¥ ) สามารถใช้การแจกแจงปกติมาตรฐานประมาณค่าการแจกแจงทวินามได้
เมื่อจำนวนครั้งของการทดลองทวินามมีขนาดใหญ่ ( n
¥ ) สามารถใช้การแจกแจงปกติมาตรฐานประมาณค่าการแจกแจงทวินามได้
ตัวอย่าง
จงหาความน่าจะเป็นที่จะได้หัว 4 ครั้งจากการโยนเหรียญ 8 ครั้ง
n = 8
x = 4 p =0.5 q=
0.5
เปิดตารางความน่าจะเป็นแบบทวินามในภาคผนวก ได้ p = 0.2734
np =
4 npq = 2
เปรียบเทียบกับการประมาณค่าแบบโค้งปกติมาตรฐาน
p
( 4,8,0.5) = p ( 3.5
– 4 <= z <= 4.5 - 4 )
Ö2
Ö 2
=
p ( -.354 <= z <= .354
) เปิดตารางได้พื้นที่
= .1368+.1368
ความน่าจะเป็นที่จะได้หัว 4 ครั้ง = .2736 ซึ่งใกล้เคียงกับการแจกแจงทวินามมาก
2. การแจกแจงแบบ
ที (t-Distribution)
ในการสุ่มตัวอย่างประชากร ถ้าประชากรมีขนาดใหญ่
การแจกแจงความน่าจะเป็นของค่าสถิติจะเข้าใกล้การแจกแจงปกติ
แต่เมื่อกลุ่มตัวอย่างมีขนาดเล็ก
การแจกแจงความน่าจะเป็นของค่าสถิติจะไม่เป็นการแจกแจงปกติแต่จะเป็นการแจกแจงแบบที
คุณสมบัติสำคัญของการแจกแจง ที
1) โค้งการแจกแจงมีลักษณะสมมาตรและระฆังคว่ำ
มีศูนย์กลางอยู่ที่ t =0
2) ค่า mean = mode = median คือ 0
3) ความน่าจะเป็นสะสม
หรือพื้นที่ใต้โค้ง = 1
4) ความแปรปรวน= df / df –2
5) การแจกแจงที จะมีค่าพิสัยตั้งแต่ - ¥ - +¥
6) การแจกแจง t จะเข้าใกล้การแจกแจงปกติมาตรฐานเมื่อ df
มีค่ามาก
เนื่องจากการใช้ค่าการแจกแจงปกติมาตรฐานประมาณค่าหรือทดสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยเลขคณิต
(m)จำเป็นต้องทราบความแปรปรวนของประชากรก่อนจึงใช้สถิติ
Z แต่ในกรณีที่ไม่ทราบค่าความแปรปรวนของประชากรกลุ่มตัวอย่างจะต้องมีขนาดใหญ่จึงจะใช้ความแปรปรวนของกลุ่มตัวอย่างประมาณค่าความแปรปรวนของประชากรได้
จึงยังสามารถใช้สถิติ Z แต่ในทางปฏิบัติมักไม่ทราบความแปรปรวนของประชากรละกลุ่มตัวอย่างที่ใช้มีขนาดเล็ก
จึงต้องใช้การแจกแจงที นอกจากนี้การแจกแจงทีก็นำไปใช้กับกลุ่มตัวอย่างขนาดใหญ่ได้เพราะการแจกแจงที
จะเข้าใกล้การแจกแจงปกติมาตรฐานที่มีค่าเฉลี่ยเลขคณิต (m) = 0 ความแปรปรวน = 1
เมื่อองศาอิสระเข้าใกล้ค่าอนันต์
3.
การแจกแจงแบบไคสแควร์ (c2 - distribution)
การแจกแจงแบบไคสแควร์
ได้มาจากการแจกแจงแบบโค้งปกติ มีหลายรูปแบบ
แต่ละรูปแบบจะกำหนดได้ ด้วยค่า df
c2 = Z2
เมื่อ
df = 1
ได้ รูปการแจกแจงใหม่
c2 = Z2 + Z2 เมื่อ
df = 2
ได้ รูปการแจกแจงใหม่
ดังรูปการแจกแจงไคสแควร์เมื่อขั้นองศาอิสระมีค่าต่างๆกัน
รูปหน้า 155 (นงนุช)
รูป 10
การแจกแจงไคสแควร์ เมื่อขั้นความเป็นอิสระ =1 , 2 , 4 , 6 , 10
การแจกแจงแบบไคสแควร์ถือว่าเป็น distribution free เพราะการนำไปใช้ไม่ต้องมีข้อตกลงเบื้องต้นเกี่ยวกับการแจกแจงของประชากร
การแจกแจงแบบไคสแควร์จึงมีประโยชน์มากมายในการทดสอบความสัมพันธ์ระหว่างตัวแปร
หรือทดสอบความเป็นอิสระ (Test of independence) การทดสอบภาวะรูปสนิทดี
(Goodness of fit) ทดสอบว่าสิ่งที่กำลังศึกษามีการแจกแจงปกติหรือไม่
นอกจากนี้ยังสามารถใช้ c2 ในการทดสอบสมมติฐานทางสถิติเกี่ยวกับความแปรปรวนของประชากรและประมาณค่าความแปรปรวนของประชากรอีกด้วย
คุณสมบัติที่สำคัญของการแจกแจงแบบไคสแควร์
1. รูปร่างเบ้ไปทางด้านบวก
ขึ้นอยู่กับdf เมื่อdf เข้าใกล้อนันต์ จะสมมาตร
2. การแจกแจงไคสแควร์ไม่มีค่าติดลบ
เพราะเป็นผลรวมกำลังสอง จึงมีค่าพิสัย ตั้งแต่ 0 ถึงอนันต์
3. พื้นที่ใต้โค้งมีค่าเท่ากับ 1
4. ความสูงของโค้งการแจกแจง( ordinate) จะมีค่าใกล้ 0 เมื่อ c2 เข้าใกล้¥
4.
การแจกแจงแบบเอฟ
(F – distribution)
การแจกแจงแบบเอฟ ได้มาจากการแจกแจงโค้งปกติ โดยนำความแปรปรวนของ 2 กลุ่มมาเปรียบเทียบกัน
กลุ่มที่ 1
m1
s21
จะได้ความสัมพันธ์
![]() S 12
= s12
c2df1
S 12
= s12
c2df1
n1 -1
กลุ่มที่ 2
m2
s22 จะได้ความสัมพันธ์
S 22 = s22
c2df2
![]() n2 –1
n2 –1
F
= c2df1/ n1 –1
โดยมี df 1 = n1 –1 และ df
2 = n 2–1
![]() c2df2/ n2 -1
c2df2/ n2 -1
การเปรียบเทียบความแตกต่างค่าเฉลี่ยเลขคณิตของกลุ่มตัวอย่างมากกว่า
2 กลุ่มขึ้นไป ถ้าใช้วิธีเปรียบเทียบกลุ่มตัวอย่าง 2
กลุ่มจะทำให้เสียเวลาเพราะต้องทดสอบทีละคู่
นอกจากนี้ยังเพิ่มความคลาดเคลื่อนชนิดที่ 1 มากกว่าที่กำหนดด้วย
ดังนั้นจึงควรใช้เทคนิคที่เรียกว่าการวิเคราะห์ความแปรปรวน(Analysis of
variance) ซึ่งต้องใช้สถิติ F ทดสอบนัยสำคัญเพื่อสรุปอ้างอิง
นอกจากนี้ยังสามารถทดสอบและประมาณค่าความแตกต่างระหว่างความแปรปรวนของประชากร 2
กลุ่ม และการทดสอบสัมประสิทธิ์สหสัมพันธ์พหุคูณ
คุณสมบัติที่สำคัญของการแจกแจงแบบเอฟ
1. การแจกแจงไม่สมมาตร
เบ้ไปทางบวก เมื่อ df เข้าใกล้อนันต์ จะสมมาตร
2. ไม่มีค่าลบ มีค่าพิสัย 0- อนันต์
3. พื้นที่ใต้โค้ง มีค่า =1
ข้อตกลงเบื้องต้นของการแจกแจงแบบเอฟ
1.
F - distribution กลุ่มตัวอย่างจะต้องสุ่มมาจากประชากรที่มีการแจกแจงปกติ
2. ความแปรปรวนของประชากรในแต่ละกลุ่มจะต้องเท่ากัน
3.
ค่าประมาณความแปรปรวน S12 และ S22 จะต้องมาจากตัวแปรสุ่มอิสระ (random variable) นั่นคือกลุ่มตัวอย่างจะต้องได้มาโดยวิธีสุ่ม
การแจกแจงความน่าจะเป็นของสถิติทดสอบแบบต่างๆ( Sampling Distribution of statistics)
การแจกแจงความน่าจะเป็นของสถิติทดสอบแบบต่างๆ
หมายถึงการแจกแจงความน่าจะเป็นของค่าสถิติได้จากกลุ่มตัวอย่างสุ่ม
ซึ่งจะบอกให้ทราบว่าค่าสถิติที่ได้จากกลุ่มตัวอย่างนั้นมีการแปรผันไปเช่นใดบ้าง
เพราะค่าสถิติเป็นตัวแปรสุ่ม กลุ่มตัวอย่างกลุ่มหนึ่งก็จะมีค่าค่าหนึ่งแตกต่างกันไป
การมีความรู้ความเข้าใจเกี่ยวกับรูปร่างลักษณะการแจกแจงของค่าสถิติของกลุ่มตัวอย่าง
มีความจำเป็นมากสำหรับวิชาสถิติ โดยเฉพาะในเรื่องการประมาณค่าและการทดสอบสมมติฐาน
การแจกแจงของค่าสถิติที่ควรรู้จักได้แก่
1. การแจกแจงค่าเฉลี่ยเลขคณิตของกลุ่มตัวอย่าง
2. การแจกแจงค่าสัดส่วนของกลุ่มตัวอย่าง
3. การแจกแจงค่าความแปรปรวนของกลุ่มตัวอย่าง
1. การแจกแจงค่าเฉลี่ยเลขคณิตของกลุ่มตัวอย่าง
(Sample Distribution of
Sample mean)
เมื่อมีการสุ่มตัวอย่างจำนวน n จากประชากรที่มีค่าเฉลี่ยเลขคณิต =m ความแปรปรวน = s2 ตามทฤษฎี
Central limit Theorem การแจกแจงของค่าเฉลี่ยเลขคณิตของกลุ่มตัวอย่าง
จะมีค่าเฉลี่ย E(X) = mx = m และความแปรปรวน (sx2) = s2/n เมื่อประชากรมีขนาดใหญ่เป็น
infinite population สุ่มตัวอย่างประชากรแบบแทนที่
และความแปรปรวน( sx2 )= s2 N-n เมื่อ มีขนาดเล็กเป็น finite population
สุ่มตัวอย่างประชากรแบบไม่แทนที่
n N-1
การแจกแจงความน่าจะเป็นของค่าเฉลี่ยเลขคณิตของกลุ่มตัวอย่าง มีคุณลักษณะ ดังนี้
1) ถ้าประชากรมีขนาดใหญ่
และมีการแจกแจงปกติ
จะทำให้การแจกแจงของค่าเฉลี่ยของกลุ่มตัวอย่างมีการแจกแจงปกติ
2) ถ้าประชากรมีขนาดใหญ่
แต่ไม่มีการแจกแจงปกติ
จะทำให้การแจกแจงของค่าเฉลี่ยของกลุ่มตัวอย่างเข้าใกล้การแจกแจงปกติ
เมื่อกลุ่มตัวอย่างมีขนาดใหญ่
3) ค่าเฉลี่ยเลขคณิตของการแจกแจงค่าเฉลี่ย
จะเท่ากับ ค่าเฉลี่ยเลขคณิตของประชากร m x = m
4) ค่าส่วนเบี่ยงเบนมาตรฐานของการแจกแจงค่าเฉลี่ยหรือค่าความคลาดเคลื่อนมาตรฐาน
คือ s x =
s/√n เมื่อประชากรมีขนาดใหญ่เป็น
infinite population สุ่มตัวอย่างประชากรแบบแทนที่
และค่าส่วนเบี่ยงเบนมาตรฐานของการแจกแจงค่าเฉลี่ยsx = s √N-n
√n √ N-1
เมื่อประชากรมีขนาดเล็กเป็น finite population สุ่มตัวอย่างประชากรแบบไม่แทนที่
รูปหน้า168
รูป 11
การแจงแจกค่าเฉลี่ยเลขคณิตของกลุ่มตัวอย่าง
ในการหาความน่าจะเป็นของประชากรและตัวอย่างประชากรที่มีขนาดใหญ่
สามารถนำตารางNormal Area Table มาใช้ โดยค่าความน่าจะเป็นก็คือพื้นที่ใต้โค้งการแจกแจงปกตินั่นเอง
![]() ค่า Z = X - m เมื่อมีการแจกแจงปกติ ค่าเฉลี่ยเลขคณิต = 0
ความแปรปรวน = 1
ค่า Z = X - m เมื่อมีการแจกแจงปกติ ค่าเฉลี่ยเลขคณิต = 0
ความแปรปรวน = 1
s/√n
แล้วนำไปเปิดค่าความน่าจะเป็นหรือพื้นที่จากตารางความน่าจะเป็นแบบปกติ
![]() ดังนั้น การคำนวณหาความน่าจะเป็นที่ X
จะมีค่าน้อยกว่า a ที่กำหนดให้หรือไม่หาได้จากสมการ
ดังนั้น การคำนวณหาความน่าจะเป็นที่ X
จะมีค่าน้อยกว่า a ที่กำหนดให้หรือไม่หาได้จากสมการ
![]()
![]() P (X< a )
= P (Z < a - m ) = P( Z < a - m )
P (X< a )
= P (Z < a - m ) = P( Z < a - m )
s x
s/√n
2. การแจกแจงค่าสัดส่วนของกลุ่มตัวอย่าง
ในบางครั้งประชากรที่สนใจอาจเป็นข้อความหรือเป็นข้อมูลเชิงคุณภาพ
โดยแบ่งประชากรออกเป็น 2
พวกหรือ 2 ลักษณะ เช่น นิสิตชาย (n1) และนิสิตหญิง(n2) โดยที่ nคือนิสิตทั้งหมด
p คือพารามิเตอร์ที่แสดงสัดส่วนของประชากร
เช่น สัดส่วนของนิสิตหญิง = n2/n
เมื่อต้องการจะประมาณค่าหรือทดสอบสมมติฐานที่เกี่ยวกับ p จะต้องเลือกกลุ่มตัวอย่างเพื่อหาค่าสัดส่วนของกลุ่มตัวอย่าง
(P) แล้วใช้สัดส่วนของกลุ่มตัวอย่างเป็นตัวประมาณค่าหรือทดสอบสมมติฐานเกี่ยวกับ
p
จากค่าเฉลี่ยและความแปรปรวนแบบทวินาม
E(X)
= S X. p(X)
= np
Var (X)
= E( X - m )2
= np(1- p)
โดยที่ X คือความสำเร็จที่เกิดขึ้น
ถ้า P คือสัดส่วนของการเกิดความสำเร็จในกลุ่มตัวอย่าง
P
=
X / n
E(P) =
E( X / n )
= 1/n . E(X)
= 1/n . n p
= p
VAR (P)
=
VAR (X / n)
= 1/n2 n.p (1- p)
= p (1- p) กรณี n มีขนาดใหญ่
n
VAR (P)
= p ( 1- p) N-n
กรณี n มีขนาดเล็ก
n
N-1
เมื่อ Sample
proportion มีการแจกแจงปกติหรือเข้าใกล้การแจกแจงปกติสามารถคำนวณความน่าจะเป็นที่สัดส่วนของกลุ่มตัวอย่างจะเท่ากับหรือน้อยกว่าค่าที่กำหนดให้ได้
เนื่องจาก
Z = P - p
sp
![]()
![]() sp =
p ( 1- p) . N-n
sp =
p ( 1- p) . N-n
√ n
N-1
![]() P (P < a ) = P ( Z < a - p
)
P (P < a ) = P ( Z < a - p
)
![]()
![]() p ( 1- p) .
N-n
p ( 1- p) .
N-n
Ö n
N-1
3. การแจกแจงค่าความแปรปรวนของกลุ่มตัวอย่าง
เมื่อมีการสุ่มตัวอย่างประชากร n มาจากประชากรที่มีการแจกแจงปกติ การแจกแจงความ
แปรปรวนของกลุ่มตัวอย่าง(S2)
จะเป็นการแจกแจงปกติ โดยมี
![]() ค่าเฉลี่ยของความแปรปรวน
m s 2 = s2(n-1)/n
ค่าเฉลี่ยของความแปรปรวน
m s 2 = s2(n-1)/n
ความแปรปรวนของค่าความแปรปรวน
s2 s 2 = s2 Ö 2/n
เมื่อ n มีขนาดใหญ่
ถ้า n มีขนาดเล็ก
การแจกแจงความแปรปรวนของกลุ่มตัวอย่างไม่เป็นการแจกแจงปกติ แต่
มีการแจกแจงแบบไคสแควร์
โดยมีองศาอิสระ = n-1
ถ้าองศาอิสระ = 1
c2(1)
= Z2
ถ้าองศาอิสระ
= n-1
c2(n-1)
= S (n-1)S2
![]() s2
s2
การคำนวณหาความน่าจะเป็นที่จะเลือกกลุ่มตัวอย่างซึ่งมี
S2 ตามที่กำหนดไว้ คือการหาพื้นที่ใต้โค้งการแจกแจงไคสแควร์นั่นเอง จากสมการ
![]() P
(S2 > a )
= P (c2
> å (n-1) a )
P
(S2 > a )
= P (c2
> å (n-1) a )
s2
การเลือกกลุ่มตัวอย่างและขนาดของกลุ่มตัวอย่าง
การเลือกกลุ่มตัวอย่างมีความจำเป็นอย่างยิ่งในทางสถิติอ้างอิง
ทั้งนี้เนื่องจากการเก็บข้อมูลกับประชากรทุกหน่วยอาจทำให้เสียเวลาและค่าใช้จ่ายที่สูงมากและบางครั้งเป็นเรื่องที่ต้องตัดสินใจภายในเวลาจำกัด
การเลือกศึกษาเฉพาะบางส่วนของประชากรจึงเป็นเรื่องที่มีความจำเป็น
เรียกว่ากลุ่มตัวอย่าง ดังนั้นกลุ่มตัวอย่าง จึงเป็นส่วนหนึ่งของประชากรที่นำมาศึกษาซึ่งเป็นตัวแทนของประชากร
การที่กลุ่มตัวอย่างจะเป็นตัวแทนที่ดีของประชากรเพื่อการอ้างอิงไปยังประชากรอย่างน่าเชื่อถือได้นั้น
จะต้องมีการเลือกตัวอย่างและขนาดตัวอย่างที่เหมาะสม
ซึ่งจะต้องอาศัยสถิติเข้ามาช่วยในการสุ่มตัวอย่างและการกำหนดขนาดของกลุ่มตัวอย่าง
ประเภทของการเลือกกลุ่มตัวอย่าง
วิธีการเลือกตัวอย่างแบ่งเป็น 2 ประเภทใหญ่ๆ คือ
1. การเลือกตัวอย่างโดยไม่ใช้ความน่าจะเป็น
( Nonprobability sampling )
เป็นการเลือกตัวอย่างโดยไม่คำนึงว่าตัวอย่างแต่ละหน่วยมีโอกาสถูกเลือกมากน้อยเท่าไร
ทำให้ไม่ทราบความน่าจะเป็นที่แต่ละหน่วยในประชากรจะถูกเลือก
การเลือกกลุ่มตัวอย่างแบบนี้ไม่สามารถนำผลที่ได้อ้างอิงไปยังประชากรได้
แต่มีความสะดวกและประหยัดเวลาและค่าใช้จ่ายมากกว่า ซึ่งสามารถทำได้หลายแบบ ดังนี้
1.1 การเลือกกลุ่มตัวอย่างแบบบังเอิญ (Accidental
sampling) เป็นการเลือกกลุ่มตัวอย่าง
เพื่อให้ได้จำนวนตามต้องการโดยไม่มีหลักเกณฑ์
กลุ่มตัวอย่างจะเป็นใครก็ได้ที่สามารถให้ข้อมูลได้
1.2 การเลือกกลุ่มตัวอย่างแบบโควต้า (
Quota sampling ) เป็นการเลือกกลุ่มตัวอย่างโดย
คำนึงถึงสัดส่วนองค์ประกอบของประชากร
เช่นเมื่อต้องการกลุ่มตัวอย่าง 100 คน ก็แบ่งเป็นเพศชาย 50 คน หญิง 50 คน แล้วก็เลือกแบบบังเอิญ คือเจอใครก็เลือกจนครบตามจำนวนที่ต้องการ
1.3 การเลือกกลุ่มตัวอย่างแบบเจาะจง ( Purposive sampling ) เป็นการเลือกกลุ่มตัวอย่างโดยพิจารณาจากการตัดสินใจของผู้วิจัยเอง
ลักษณะของกลุ่มที่เลือกเป็นไปตามวัตถุประสงค์ของการวิจัย
การเลือกกลุ่มตัวอย่างแบบเจาะจงต้องอาศัยความรอบรู้
ความชำนาญและประสบการณ์ในเรื่องนั้นๆของผู้ทำวิจัย
การเลือกกลุ่มตัวอย่างแบบนี้มีชื่อเรียกอีกอย่างว่า Judgement sampling
2. การเลือกตัวอย่างโดยใช้ความน่าจะเป็น (
Probability sampling )
เป็นการเลือกตัวอย่างโดยสามารถกำหนดโอกาสที่หน่วยตัวอย่างแต่ละหน่วยถูกเลือก
ทำให้ทราบความน่าจะเป็นที่แต่ละหน่วยในประชากรจะถูกเลือก
การเลือกกลุ่มตัวอย่างแบบนี้สามารถนำผลที่ได้อ้างอิงไปยังประชากรได้ สามารถทำได้หลายแบบ ดังนี้
2.1 การสุ่มตัวอย่างแบบง่าย (Simple
random sampling) เป็นการสุ่มตัวอย่างโดยถือว่าทุกๆหน่วยหรือทุกๆสมาชิกในประชากรมีโอกาสจะถูกเลือกเท่าๆกัน
การสุ่มวิธีนี้จะต้องมีรายชื่อประชากรทั้งหมดและมีการให้เลขกำกับ
วิธีการอาจใช้วิธีการจับสลากโดยทำรายชื่อประชากรทั้งหมด
หรือใช้ตารางเลขสุ่มโดยมีเลขกำกับหน่วยรายชื่อทั้งหมดของประชากร
วิธีการจับสลาก
โดยทำสลากแบบเดียวกันมีหมายเลขกำกับตามหน่วยย่อยของประชากร ตั้งแต่เลข 1 ถึงเลขสุดท้ายซึ่งเท่ากับจำนวนประชากร แล้วทำการสุ่มจับสลากขึ้นมาทีละใบ
จนครบตามขนาดของกลุ่มตัวอย่างที่ต้องการ
วิธีการใช้ตารางเลขสุ่ม
โดยมีบัญชีรายชื่อของทุกหน่วยย่อยของประชากร
กำหนดหมายเลขประจำหน่วยย่อยของประชากร แล้วกำหนดกฎเกณฑ์การใช้ตารางเลขสุ่ม
เช่น สุ่มหลัก (Column) และสุ่มแถว(Row) ของตัวเลขเริ่มต้น แล้วอ่านจากซ้ายไปขวา เมื่อจบแถวให้ขึ้นแถวใหม่ ถ้าได้หมายเลขซ้ำต้องตัดออก
จนได้จำนวนครบตามที่ต้องการ
2.2 การสุ่มตัวอย่างแบบเป็นระบบ ( Systematic sampling) เป็นการสุ่มตัวอย่างโดยมีรายชื่อของทุกหน่วยประชากรมาเรียงเป็นระบบตามบัญชีเรียกชื่อ
การสุ่มจะแบ่งประชากรออกเป็นช่วงๆที่เท่ากันอาจใช้ช่วงจากสัดส่วนของขนาดกลุ่มตัวอย่างและประชากร
แล้วสุ่มประชากรหน่วยแรก ส่วนหน่วยต่อๆไปนับจากช่วงสัดส่วนที่คำนวณไว้ เช่น ต้องการสุ่มนิสิต250คน จากนิสิตทั้งหมด 3000 คน ดังนั้นจึงสุ่มทุกๆ 12
คน เอามา 1 คน
สมมติเมื่อสุ่มผู้ที่ตกเป็นตัวอย่างคนแรก ได้หมายเลข 0005 คนที่สองได้แก่หมายเลข 0017 คนที่สามได้แก่หมายเลข 0029
และคนต่อๆไปจะได้หมายเลข 0041
,0053,0065,…2993
จนครบ 250 คน
2.3 การสุ่มตัวอย่างแบบชั้นภูมิ (Stratified sampling) เป็นการสุ่มตัวอย่างโดยแยกประชากรออกเป็นกลุ่มประชากรย่อยๆ
หรือแบ่งเป็นชั้นภูมิก่อน โดยหน่วยประชากรในแต่ละชั้นภูมิจะมีลักษณะเหมือนกัน (homogenious) แล้วสุ่มอย่างง่ายจากแต่ละชั้นเพื่อให้ได้จำนวนกลุ่มตัวอย่างตามสัดส่วนของขนาดกลุ่มตัวอย่างและกลุ่มประชากร
2.4
การสุ่มตัวอย่างแบบกลุ่ม (Cluster sampling ) เป็นการสุ่มตัวอย่างโดยแบ่งประชากร
ออกตามพื้นที่โดยไม่จำเป็นต้องทำบัญชีรายชื่อของประชากร
และสุ่มตัวอย่างประชากรจากพื้นที่ดังกล่าวตามจำนวนที่ต้องการ
แล้วศึกษาทุกหน่วยประชากรในกลุ่มพื้นที่นั้นๆ
หรือจะทำการสุ่มต่อเป็นลำดับขั้นมากกว่า 1 ระดับ โดยอาจแบ่งพื้นที่จากภาค เป็นจังหวัด จาก จังหวัดเป็นอำเภอ
และเรื่อยไปจนถึงหมู่บ้าน
นอกจากนี้การสุ่มตัวอย่างยังสามารถเลือกสุ่มตัวอย่างผสมระหว่างแบบง่าย
แบบชั้นภูมิและแบบกลุ่มด้วยก็ได้
ขนาดของกลุ่มตัวอย่าง
ขนาดของกลุ่มตัวอย่างมีความสำคัญอย่างมาในการวิจัยเมื่อกลุ่มตัวอย่างมีความเหมาะสมข้อมูลที่ได้จากกลุ่มตัวอย่างมีมากพอก็จะทำให้ผลงานวิจัยนั้นมีคุณค่า
ขนาดของกลุ่มตัวอย่างเท่าไรจึงจะเหมาะสมกับการวิจัยขึ้นอยู่กับการวิจัยว่าจะยอมให้เกิดความคลาดเคลื่อนมากน้อยเพียงใด
จึงจะยอมรับได้ การหาขนาดตัวอย่างสามารถคำนวณได้จากสูตร ในกรณีต่างๆ ได้ดังนี้
1. การประมาณค่าเฉลี่ยเลขคณิตของประชากร
ยอมให้เกิดความคลาดเคลื่อน e หน่วย ที่
ระดับความเชื่อมั่น
(1- µ)%
1.1
ในกรณีที่ประชากรมีจำนวนไม่แน่นอน (Infinite population)
![]()
![]() จาก
Z
= X - m
จาก
Z
= X - m
sx
![]() sx
= s/Ö n
sx
= s/Ö n
![]()
![]()
![]() ทำให้ได้
n = Z2 s2
ทำให้ได้
n = Z2 s2
![]() (X - m)2
(X - m)2
ดังนั้น n = Z2 s2
![]()
![]() e2
e2
e คือความคลาดเคลื่อนที่ยอมให้เกิดขึ้นหรือความแตกต่างระหว่าง
X - m
ตัวอย่าง สำนักงานสถิติแห่งชาติ ประกาศว่าโดยเฉลี่ยแล้วค่าใช้จ่ายต่อเดือนของครอบครัวขนาดกลางมีค่าเบี่ยงเบนมาตรฐานเท่ากับ
1,200 บาท
ถ้าต้องการประมาณค่าใช้จ่ายของครอบครัวขนาดกลาง
โดยยอมให้แตกต่างจากค่าใช้จ่ายที่แท้จริง 50
บาทที่ระดับความเชื่อมั่น 95 % จะต้องเลือกตัวอย่างครอบครัวขนาดกลางมากี่ครอบครัว
s = 1,200
e = 50
Z = 1.96
![]() n = Z2 s2
n = Z2 s2
e2
![]() ขนาดตัวอย่าง(n) = (1.96)2 (1200) 2
ขนาดตัวอย่าง(n) = (1.96)2 (1200) 2
502
= 2212.76
จะต้องเลือกตัวอย่างครอบครัวมา 2213 ครอบครัว
1.2
ในกรณีที่ประชากรมีจำนวนแน่นอน (Finite population) Yamane( 1973)
ได้คิดสูตรที่ใช้ในการคำนวณขนาดของกลุ่มตัวอย่าง คือ
![]() n
= N
n
= N
1+Ne2
e คือความคลาดเคลื่อนที่ยอมให้เกิดขึ้นในรูปของสัดส่วน
ตัวอย่าง ถ้าประชากรที่ศึกษามี 1,800 คน และต้องการให้เกิดความคลาดเคลื่อนในการสุ่มตัวอย่างร้อยละ 5 ขนาดของกลุ่มตัวอย่างควรเป็นเท่าไร
![]() สูตรที่ใช้ในการคำนวณขนาดของกลุ่มตัวอย่าง
คือ n = N
สูตรที่ใช้ในการคำนวณขนาดของกลุ่มตัวอย่าง
คือ n = N
1+Ne2
=
1,800
= 327
1+1,800(.05) 2
จะต้องเลือกตัวอย่าง 327 คน
2.
การประมาณค่าสัดส่วนของประชากร(p) ยอมให้เกิดความคลาดเคลื่อน e % ที่
ระดับความเชื่อมั่น
(1- µ)%
2.1 ในกรณีที่ทราบค่า p
จาก
Z = P - p
sp
![]()
![]() sp = p ( 1- p)
sp = p ( 1- p)
√ n
![]() ดังนั้น
n
= Z 2 p ( 1- p)
ดังนั้น
n
= Z 2 p ( 1- p)
e2
ตัวอย่าง ถ้าต้องการประมาณค่าสัดส่วนของคนกทม.ที่มีบ้านเป็นของตนเองในปีนี้ให้ผิดพลาดไม่เกิน
3 % ด้วยระดับความเชื่อมั่น 90 % ควรสุ่มตัวอย่างคนในกทม.มากี่คน ถ้าทราบว่าเปอร์เซ็นต์ของคนที่มีบ้านเป็นของตนเองเมื่อ 2 ปีที่ผ่านมา เท่ากับ 60%
p = .60
1- p = 1-0.6 = 0.4
e = 0.03
Z = 1.645 (ที่ระดับความเชื่อมั่นเท่ากับ
90 %)
![]() n = Z2 p ( 1- p)
n = Z2 p ( 1- p)
e2
![]() =
(1.645)2 .60 (0.4) = 721.6
=
(1.645)2 .60 (0.4) = 721.6
(0.03) 2
ดังนั้นควรสุ่มตัวอย่างคนในกทม.
= 721 คน
ในกรณีที่ไม่ทราบค่า p Yamane ได้หาค่า p ( 1- p) ดังนี้
p ( 1- p)จะมีค่ามากที่สุดเมื่อ p = ½ คือp ( 1- p) = 1/4
![]() ดังนั้น
n
=
Z 2
ดังนั้น
n
=
Z 2
4 e2
ตัวอย่าง ในการสำรวจความคิดเห็นของนิสิตคณะครุศาสตร์ที่มีต่อวิชาชีพครู
ถ้าต้องการให้เกิดความผิดพลาด 2% ที่ระดับความเชื่อมั่น 90% ควรสอบถามนิสิตคณะครุศาสตร์กี่คน
e = 0.02
Z
= 1.645
![]() n
= Z2
n
= Z2
4 e2
= (1.645) 2 = 1691.265
4(0.02) 2
จะต้องสอบถามจากนิสิต
1691
คน
การประมาณค่า ( Estimation )
การประมาณค่า
เป็นวิธีการวิเคราะห์ทางสถิติที่มีความสำคัญมาก
จะพบว่าในปัจจุบันมีการใช้การประมาณค่าในทุกๆองค์กร
เช่นประมาณผลสัมฤทธิ์ทางการเรียนของนักเรียน เพื่อวางแผนการจัดการเรียนการสอน
เป็นต้น การประมาณค่าต่างๆ คือ การประมาณค่าพารามิเตอร์ของประชากร เช่น
ค่าเฉลี่ยประชากร(m) ค่าสัดส่วนประชากร (p) ค่าความแปรปรวนของประชากร(s2) โดยใช้ข้อมูลจากกลุ่มตัวอย่าง
ประเภทของการประมาณค่า แบ่งเป็น 2 ประเภท คือ
1. การประมาณค่าแบบจุด (Point
Estimation) เป็นการประมาณค่าพารามิเตอร์
ด้วยเลขตัวใดตัวหนึ่งโดยใช้ข้อมูลจากกลุ่มตัวอย่าง เช่น
ใช้ค่าเฉลี่ยของตัวอย่างประมาณค่าเฉลี่ยของประชากร
ตัวอย่างคือการประมาณค่ารายได้เฉลี่ยของคนในประเทศด้วยรายได้เฉลี่ยของคนในกรุงเทพ
เป็นต้น ค่าประมาณแบบจุดนี้อาจจะมีค่าเท่ากับพารามิเตอร์หรือไม่ก็ได้
และมีโอกาสคลาดเคลื่อนไปจากค่าพารามิเตอร์ได้มาก
การประมาณค่าพารามิเตอร์แบบจุด
|
ประชากรที่มีการแจกแจงแบบใดๆ |
พารามิเตอร์ที่ต้องการประมาณ |
ค่าประมาณแบบจุด |
|
m
p s2 m 1 - m 2 p1 - p2 |
X P S2 X1
– X2 P1 - P2 |
2. การประมาณค่าแบบช่วง ( Interval
Estimation) เป็นการประมาณค่าพารามิเตอร์ว่าอยู่ในช่วงใดช่วงหนึ่ง
โดยใช้ข้อมูลจากกลุ่มตัวอย่าง
โดยที่ช่วงของการประมาณค่าจะบอกค่าต่ำสุดและสูงสุด เช่น
ใช้ช่วงของค่าเฉลี่ยของตัวอย่างประมาณค่าเฉลี่ยของประชากร
ซึ่งมีโอกาสคลาดเคลื่อนไปจากค่าพารามิเตอร์ได้น้อยกว่าการประมาณค่าแบบจุด
การประมาณค่าแบบช่วงนี้
ค่าต่ำสุดและค่าสูงสุดจะขึ้นอยู่กับระดับความเชื่อมั่น (Level of Confidence) ช่วงของการประมาณค่าจะกว้างหรือแคบขึ้นอยู่กับระดับความเชื่อมั่นและการกระจายของลักษณะประชากรที่สนใจศึกษา
ถ้าระดับความเชื่อมั่นสูงและลักษณะที่สนใจศึกษามีการกระจายมาก ช่วงของค่าประมาณจะกว้าง
ถ้าระดับความเชื่อมั่นต่ำและลักษณะที่สนใจศึกษามีการกระจายน้อย
ช่วงของค่าประมาณจะแคบ
ระดับความเชื่อมั่น หมายถึง
โอกาสที่พารามิเตอร์ของประชากรจะอยู่ในช่วงของค่าที่ประมาณได้ เช่น p ( L< m< U
) = .95 หมายถึง โอกาสที่ m จะอยู่ในช่วงของ L และ
U เท่ากับ 95% และ p ( m < L ) + p ( m > U )
= .05
หมายถึง โอกาสที่ m จะน้อยกว่า L และมากกว่า U เท่ากับ 5%
การประมาณค่าเฉลี่ยของประชากร ( m ) แบบช่วง
พิจารณาจาก 3 กรณี
1.
ประชากรที่มีการแจกแจงแบบปกติ ทราบค่าความแปรปรวนของประชากร
2.
ประชากรที่มีการแจกแจงแบบใดๆ กลุ่มตัวอย่างมีขนาดใหญ่ (
n ³ 30)
3.
ประชากรที่มีการแจกแจงแบบปกติหรือใกล้เคียง
ไม่ทราบค่าความแปรปรวนของประชากรและกลุ่มตัวอย่างมีขนาดเล็ก ( n £ 30)
1. ประชากรที่มีการแจกแจงแบบปกติ
ทราบค่าความแปรปรวนของประชากร
ต้องการประมาณค่าเฉลี่ยประชากร (m ) จากค่าเฉลี่ยตัวอย่าง (X)
X ~ normal( m , s2 / n )
p ( L< m< U ) = 1- µ
แปลง X ให้เป็น Z
Z = ( X - m ) / s
Ö n
1-
µ = p (-Z 1- µ / 2
< Z < Z 1- µ / 2)
= p ( -Z 1- µ / 2< X - m / s
< Z1- µ / 2)
Ö n
= p ( -Z 1 - µ / 2 s < X - m
< Z 1 - µ / 2
s ) สมการ
1
Ö n
Ö n
จากสมการ 1 แยกได้ 2 สมการย่อย
X - m < Z 1- µ / 2 s )
และ
X - m > -Z
1 - µ / 2 s
Ö n
Ö n
X – Z 1- µ / 2 s ) < m
และ
X + Z 1 - µ / 2 s > m
Ö n
Ö n
ดังนั้น
p (X - Z
1- µ / 2
s < m
< X + Z 1 - µ / 2 s )
= 1- µ
Ö n
Ö n
สรุป ค่าประมาณค่าเฉลี่ยประชากร แบบช่วง
ที่ระดับความเชื่อมั่น( 1- µ) = X ± Z1- µ / 2 s
Ön
ในทำนองเดียวกัน
ประชากรที่มีการแจกแจงแบบใดๆ กลุ่มตัวอย่างมีขนาดใหญ่ ( n ³ 30)
และประชากรที่มีการแจกแจงแบบปกติหรือใกล้เคียงแต่ไม่ทราบค่าความแปรปรวนของประชากรและกลุ่มตัวอย่างมีขนาดเล็ก
( n < 30) ตลอดจนการประมาณค่าสัดส่วนประชากร
(p) ค่าความแปรปรวนของประชากร(s2) สรุปค่าประมาณแบบช่วงจากประชากรกลุ่มเดียวและสองกลุ่มได้จากตารางดังต่อไปนี้
สรุปค่าประมาณแบบช่วง
|
พารามิเตอร์ที่ต้องการประมาณค่าของประชากรเดียว |
ค่าประมาณแบบช่วง |
การประมาณค่าเฉลี่ยประชากร
m แบบช่วง
1. ประชากรมีการแจกแจงแบบปกติและทราบค่า
s2 2. ประชากรมีการแจกแจงแบบใดๆตัวอย่างมีขนาดใหญ่
(n³30) 2.1 ทราบค่า s2 2.2 ไม่ทราบค่า s2 3. ประชากรมีการแจกแจงแบบปกติแต่ไม่ทราบค่า
s2 ตัวอย่างมีขนาดเล็ก (n < 30 ) |
X
± Z 1- µ / 2 s /
Ö n X
± Z 1 - µ / 2 s /
Ö n X
± Z 1 - µ / 2 s / Ö n X
± t 1 - µ / 2; n-1 s / Ö n |
การประมาณค่าสัดส่วนประชากร
pแบบช่วง
ประชากรมีการแจกแจงแบบใดๆตัวอย่างมีขนาดใหญ่ (n³30) |
P
± Z 1 - µ / 2 Öpq/ n |
|
การประมาณค่าความแปรปรวนประชากร s2แบบช่วง ประชากรมีการแจกแจงแบบปกติ |
( n-1) s2 , ( n-1) s2 c21 - µ / 2
c2 µ / 2 |
|
พารามิเตอร์ที่ต้องการประมาณค่าของสองประชากร |
ค่าประมาณแบบช่วง |
|
การประมาณค่าผลต่างระหว่างค่าเฉลี่ยของสองประชากรที่มีการสุ่มตัวอย่างสองชุดอย่างเป็นอิสระ 1.
ประชากรมีการแจกแจงแบบปกติและทราบค่า s12 และ s22 2.
ประชากรมีการแจกแจงแบบใดๆตัวอย่างมีขนาดใหญ่ (n1,
n2³30) 2.1 ทราบค่า s12 และ s22 2.2 ไม่ทราบค่า s12 และ s22 |
X1-X
2 ± Z 1-
µ / 2Ö s12/ n1+s22/n2 X1-X
2 ± Z1- µ / 2 Ö s12/ n1+s22/n2 X1-
X 2 ± Z1- µ / 2 Ö S12/
n1+S22/n2 |
|
3. ประชากรมีการแจกแจงแบบปกติแต่ไม่ทราบค่า
s12 และ s22 ตัวอย่างมีขนาดเล็ก (n1, n2 < 30 ) 3.1 ไม่ทราบค่า s12 และ s22 แต่ทราบว่า s12 = s22 |
X1-
X 2 ± t 1 -
µ / 2 SpÖ1/n1+1/n2 t
1 - µ / 2 ที่องศาอิสระ n1+n2-2 Sp
= ( n1-1) S12+ ( n2-1) S22
n1+n2-2 |
|
พารามิเตอร์ที่ต้องการประมาณค่าของสองประชากร |
ค่าประมาณแบบช่วง |
|
3.2 ไม่ทราบค่า s12 และ s22 แต่ทราบว่า s12 ¹ s22 |
X1-
X 2 ± t 1-
µ / 2 ÖS12/ n1+ S22/n2 t 1 - µ / 2 ที่องศาอิสระ g g =
( S12/ n1+ S22/n2)
2 (S12/
n1) 2+ (S22/n2)
2
n1-1 n2- 2 |
![]()
|
พารามิเตอร์ที่ต้องการประมาณค่าของสองประชากร |
ค่าประมาณแบบช่วง |
|
การประมาณค่าผลต่างระหว่างค่าเฉลี่ยของสองประชากรแบบจับคู่ ประชากรมีการแจกแจงแบบปกติหรือใกล้เคียง n < 30 |
d ± t 1 -
µ / 2; n-1 Sd / Ö n d
i= x 1I – x 2I d
=ådi /
n , Sd2=å( di - d) 2/ ( n-1) |
|
การประมาณค่าผลต่างระหว่างค่าสัดส่วนสองประชากร (n1,
n2³30) |
(p1-
p2) +Z1 - µ / 2 Öp1q1/n1+ p2q2/n2 |
|
|
S12
1 S12
F 1- µ / 2; n2-1,n1-1
|
การทดสอบสมมติฐาน
(Test of Hypothesis)
สมมติฐาน
คือสิ่งที่คาดว่าจะเกิดขึ้นหรือคำตอบที่คาดว่าจะได้รับจากการศึกษา
สมมติฐานจึงมักเป็นข้อสมมุติที่สมเหตุสมผลจากแนวคิดทฤษฎีที่เสนอขึ้นมา
แล้วใช้เป็นแนวทางในการสืบสวนค้นคว้า เพื่อทำการตรวจสอบความถูกต้องของสมมติฐาน สมมติฐานที่ใช้อยู่ในการวิจัยจำแนกเป็น 2 ประเภทใหญ่ๆ คือ
1.
สมมติฐานทางการวิจัย ( Research Hypothesis ) หมายถึง
ข้อความที่เป็นความคาดหวังหรือเป็นคำตอบของการวิจัยไว้ล่วงหน้าโดยอาศัยประสบการณ์
หลักการ ทฤษฎีต่างๆ ซึ่งอาจจะถูกหรือผิดไปจากผลการวิจัยก็ได้
2.
สมมติฐานทางสถิติ (Statistical
Hypothesis ) หมายถึง
ข้อความที่เกี่ยวข้องกับค่าพารามิเตอร์ที่ยังไม่ทราบค่า การตั้งสมมติฐานทางสถิติเพื่อการทดสอบจะต้องประกอบด้วยสมมติฐาน 2 ชนิดทุกครั้ง คือ
1. สมมติฐานว่าง ( Null
Hypothesis ) ใช้สัญลักษณ์
Ho คือ
สมมติฐานที่ระบุความไม่แตกต่างกันของค่าพารามิเตอร์ จะเห็นว่าสมมติฐานว่าง
จะมีเครื่องหมาย เท่ากับ ปรากฏอยู่เสมอ เช่น
Ho : m = 10,000 หมายถึง
ค่าเฉลี่ยของกลุ่มประชากรมีค่าเท่ากับ 10,000
Ho : m1 = m2 หมายถึง ค่าเฉลี่ยของกลุ่มประชากรกลุ่มที่
1
เท่ากับค่าเฉลี่ยของกลุ่มประชากร กลุ่มที่ 2
2. สมมติฐานแย้ง ( Alternative
Hypothesis ) ให้สัญลักษณ์ Ha หรือ H1 หมายถึง ข้อความ
ที่ตรงข้ามกับสมมติฐานว่างที่ต้องการทดสอบ
ซึ่งเขียนในลักษณะที่แสดงความแตกต่างของค่าพารามิเตอร์ที่ต้องการทดสอบ โดยที่สมมติฐานว่างและสมมติฐานแย้ง
จะอยู่ในทิศทางที่ตรงกันข้ามเสมอ
แบ่งเป็น 2 แบบ
2.1
สมมติฐานทางเลือกที่ไม่แสดงทิศทางของความแตกต่างระหว่างค่าพารามิเตอร์ที่ต้องการทดสอบ ใช้สำหรับการทดสอบ 2
ทาง (Two- tailed Test ) เช่น
Ho : m1
= m2 ( สมมติฐานว่าง )
H1 : m1 ¹ m2 ( สมมติฐานแย้ง )
2.2
สมมติฐานทางเลือกที่แสดงทิศทางของความแตกต่างระหว่างค่าพารามิเตอร์ที่ต้องการทดสอบ
เป็นการกล่าวถึงพารามิเตอร์อย่างเจาะจงว่ามีค่ามากกว่าหรือน้อยกว่า
จึงใช้สำหรับการทดสอบทางเดียว (One-
tailed Test ) เช่น
Ho : m1 = m 2 ( สมมติฐานว่าง
)
H1 : m1
> m 2 ( สมมติฐานแย้ง
) หรือ
H1
: m1
< m 2
นอกจากนี้ยังสามารถเขียนการเขียนสมมติฐานทางสถิติในรูปของข้อความได้ด้วย
เช่น
Ho : รายได้เฉลี่ยต่อเดือนของคนไทยเป็น
10,000 บาท
H1 : รายได้เฉลี่ยต่อเดือนของคนไทยไม่เท่ากับ
10,000 บาท
ตัวอย่าง การเขียนสมมติฐาน
บริษัทผู้ผลิตหลอดไฟแห่งหนึ่งอ้างว่าหลอดไฟของเขาจะมีอายุการใช้งานเฉลี่ยนานกว่า1,000 ชั่วโมง
และคาดว่าคำอ้างเป็นจริง สมมติฐานจะเขียนได้เป็น
Ho : m
= 1000
H1
: m
> 1000
ถ้าคาดว่าคะแนนเฉลี่ยของนักเรียน ม.1 / a เท่ากับนักเรียน ม.1 /
b สมมติฐานจะเขียนได้เป็น
Ho : ma = mb
H1
: ma ¹
mb
การทดสอบสมมติฐานทางสถิติ
การทดสอบสมมติฐานทางสถิติ
เป็นการตัดสินใจผลที่ได้จากการเปรียบเทียบระหว่างค่าสถิติที่ได้จากกลุ่มตัวอย่างกับค่าพารามิเตอร์ตามสมมติฐานว่างที่กำหนดไว้ล่วงหน้า
(สมมติค่าพารามิเตอร์ของประชากร) โดยอาศัยเกณฑ์ที่ตั้งไว้ ผลที่ได้จากการทดสอบสมมติฐานทางสถิติ มี 2 ลักษณะ คือ
1) การยอมรับหรือคงสมมติฐาน
หมายความว่า
ความแตกต่างของค่าสถิติที่คำนวณได้จากกลุ่มตัวอย่างกับค่าพารามิเตอร์ตามสมมติฐานว่าง
มีขนาดต่างกันเล็กน้อยและความแตกต่างนั้นอยู่ภายในขอบเขตที่ยอมรับได้
และถือได้ว่าเป็นความแตกต่างโดยบังเอิญอันเนื่องมาจากความคลาดเคลื่อนจากการสุ่มตัวอย่างหรือลักษณะเฉพาะของกลุ่มตัวอย่างประชากรนั้น
อันมิใช่ความแตกต่างที่แท้จริง จึงกล่าวได้ว่าการทดสอบไม่มีนัยสำคัญ
จึงยอมรับหรือคงสมมติฐานว่างไว้
2) การปฏิเสธสมมติฐาน หมายความว่า
ความแตกต่างของค่าสถิติที่คำนวณได้จากกลุ่มตัวอย่างกับค่าพารามิเตอร์ตามสมมติฐานว่าง
มีขนาดต่างกันมากและความแตกต่างนั้นมากเกินขอบเขตที่ยอมรับได้
และถือได้ว่าเป็นความแตกต่างที่แท้จริง ไม่ใช่บังเอิญ
จึงกล่าวได้ว่าการทดสอบมีนัยสำคัญ
จึงปฏิเสธสมมติฐานว่างที่ตั้งไว้และยอมรับสมมติฐานแย้ง
ความผิดพลาดในการทดสอบสมมติฐานทางสถิติ
เนื่องจากการตัดสินใจยอมรับหรือปฏิเสธสมมติฐานว่าง
ขึ้นอยู่กับสถิติที่ใช้ทดสอบ ซึ่งคำนวณได้จากกลุ่มตัวอย่างมิใช่จากกลุ่มประชากร
จึงอาจทำให้การตัดสินใจถูกต้องหรืออาจเกิดความคลาดเคลื่อนได้ ดังนี้
1. ความผิดพลาดประเภทที่ 1 (Type I
Error ) เป็นความผิดพลาดเนื่องจากการปฏิเสธ
Ho
หรือไม่ยอมรับ Ho เมื่อ Ho เป็นจริง ใช้สัญลักษณ์ a โดยที่a = P ( ปฏิเสธ Ho
โดยที่ Ho เป็นจริง )
2. ความผิดพลาดประเภทที่ 2 (
Type II Error ) เป็นความผิดพลาดเนื่องจากการยอมรับ
Ho
โดยที่ Ho ไม่เป็นจริง
และใช้สัญลักษณ์ b แทนความผิดพลาดประเภทนี้ โดยที่ b = P ( ยอมรับ Ho
โดยที่ Hoไม่เป็นจริง )
แสดงผลการทดสอบและความผิดพลาดในการทดสอบ
ผลการทดสอบ
|
ความเป็นจริง |
|
|
Ho เป็นจริง |
Ho
ไม่เป็นจริง |
|
ยอมรับ Ho
|
ผลการทดสอบถูกต้อง |
ความผิดพลาดประเภทที่ 2 (b) |
ปฏิเสธ Ho
|
ความผิดพลาดประเภทที่ 1 (a) |
ผลการทดสอบถูกต้อง |
ระดับความมีนัยสำคัญ
ระดับความมีนัยสำคัญ หมายถึง ความน่าจะเป็นในการปฏิเสธสมมติฐานว่างที่ถูก
จึงเป็นโอกาสของความคลาดเคลื่อนประเภทที่ 1 โดยทั่วไปนิยมใช้สัญลักษณ์ a แทนระดับการมีนัยสำคัญ เช่น a=0.05
ระดับความเชื่อมั่น
ระดับความเชื่อมั่น หมายถึง
ความน่าจะเป็นในการยอมรับสมมติฐานว่างที่ถูก (1-a) โดยทั่วไปนิยมคำนวณเป็น ค่าร้อยละ เช่น
ระดับความเชื่อมั่นเท่ากับ 95 %
บริเวณวิกฤตหรือเขตการปฏิเสธ (Critical Region)
บริเวณวิกฤต (Critical Region) เป็นขอบเขตที่กำหนดตามระดับการมีนัยสำคัญ
ถ้าค่าสถิติที่คำนวณได้ตกอยู่ในขอบเขตนี้ ถือว่าการทดสอบนั้นมีนัยสำคัญ (Significance)
หลักการทดสอบสมมติฐานทางสถิติ
การทดสอบสมมติฐานทางสถิติ
เป็นการตัดสินใจเชิงสถิติเกี่ยวกับค่าพารามิเตอร์ของประชากรว่ามีความแตกต่างกันหรือไม่ ด้วยการใช้ข้อมูลค่าสถิติจากกลุ่มตัวอย่างเพื่อคำนวณค่าสถิติทดสอบและตัดสินใจคงสมมติฐานว่างหรือปฏิเสธสมมติฐานว่างตามหลักเกณฑ์ที่กำหนด ทำให้สามารถสรุปผลเกี่ยวกับค่าพารามิเตอร์ของประชากรได้
ขั้นตอนของการทดสอบสมมติฐาน
ขั้นที่1 ตั้งสมมติฐานเพื่อการทดสอบ
สำหรับการทดสอบแบบทางเดียว หรือ สองทางโดยตั้งสมมติฐาน Ho และ H1
ขั้นที่2 กำหนดสถิติเพื่อการทดสอบ
1)
การทดสอบเกี่ยวกับค่าเฉลี่ยของประชากร 1 กลุ่ม ใช้สถิติทดสอบ Z และ t-test
2) การทดสอบเกี่ยวกับค่าเฉลี่ยของประชากร 2 กลุ่ม ใช้สถิติทดสอบ Z
และ t-test
ขั้นที่3 คำนวณค่าสถิติทดสอบ
โดยนำข้อมูลที่ได้มาแทนค่าในสูตรคำนวณค่าสถิติทดสอบ
ขั้นที่4 กำหนดระดับนัยสำคัญ
โดยทั่วไปมักกำหนดให้ค่า a เท่ากับ 0.01 หรือ0.05
ขั้นที่5
กำหนดบริเวณวิกฤตที่เป็นเขตปฏิเสธสมมติฐาน Ho
คือการหาค่าวิกฤต
ซึ่งเป็นค่าที่แบ่งเขตปฏิเสธและเขตยอมรับ Ho ค่าวิกฤตนี้ขึ้นอยู่กับประเภทของการทดสอบ
ว่าเป็นการทดสอบแบบทางเดียวหรือสองทาง
การกำหนดบริเวณวิกฤตแบบทางเดียว
H0 : m £ m o
หรือ
2. H0 : m ³ m o
H1 : m > m o H1
: m < m o
![]()
![]()
![]()

![]()
![]() ช่วงความเชื่อมั่น a a ช่วงความเชื่อมั่น
ช่วงความเชื่อมั่น a a ช่วงความเชื่อมั่น
![]()
![]()
![]()
![]() 0
บริเวณวิกฤต
บริเวณวิกฤต
0
0
บริเวณวิกฤต
บริเวณวิกฤต
0
ค่าวิกฤต
ค่าวิกฤต
การกำหนดบริเวณวิกฤตแบบสองทาง
H0 : m = m o
H1 : m ¹ m o
![]()
![]()

 a/ 2
ช่วงความเชื่อมั่น
a/ 2
a/ 2
ช่วงความเชื่อมั่น
a/ 2
![]()
![]()
![]()
![]()
![]() บริเวณวิกฤต
0 บริเวณวิกฤต
บริเวณวิกฤต
0 บริเวณวิกฤต
ค่าวิกฤต
ขั้นที่6 สรุปผลการทดสอบ โดยนำค่าสถิติทดสอบที่คำนวณได้จากขั้นที่
3 มาเปรียบเทียบกับค่าวิกฤต ในขั้นที่ 5 ถ้าค่าสถิติทดสอบอยู่ในเขตปฏิเสธ จะสรุปว่าปฏิเสธ Ho แต่ถ้าค่าสถิติทดสอบอยู่ในเขตยอมรับ จะสรุปว่ายอมรับ Ho
ประเภทของการทดสอบสมมติฐาน
การทดสอบสมมติฐานทางสถิติ แบ่งเป็น
1. การทดสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยของประชากรเดียว (m )
1.
การทดสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยประชากรเมื่อประชากรมีการแจกแจงแบบปกติ
และทราบค่า
แปรปรวนประชากร
สมมติฐาน
H0 : m £ m o หรือ 2. H0 : m ³ m o หรือ 3. H0 : m = m o
H1 : m > m o
H1
: m < m o
H1 : m ¹ m o
 สถิติทดสอบ
Z
= C -
m o
สถิติทดสอบ
Z
= C -
m o
![]() s / Ö n
s / Ö n
 2.
การทดสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยประชากร เมื่อประชากรมีการแจกแจงแบบใด ๆ
และขนาดตัวอย่างใหญ่ (> 30 )
เมื่อทราบค่าแปรปรวนประชากร
2.
การทดสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยประชากร เมื่อประชากรมีการแจกแจงแบบใด ๆ
และขนาดตัวอย่างใหญ่ (> 30 )
เมื่อทราบค่าแปรปรวนประชากร
![]() สถิติทดสอบ
Z = C -
m o
สถิติทดสอบ
Z = C -
m o
s / Ö n
เมื่อไม่ทราบค่าแปรปรวนประชากร
 Z = C - m o
Z = C - m o
![]() s / Ö n
s / Ö n
 3. การทดสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยประชากร
เมื่อไม่ทราบค่าแปรปรวนประชากรและตัวอย่างมีขนาดเล็ก ( n < 30 )
3. การทดสอบสมมติฐานเกี่ยวกับค่าเฉลี่ยประชากร
เมื่อไม่ทราบค่าแปรปรวนประชากรและตัวอย่างมีขนาดเล็ก ( n < 30 )
![]() t = C - m o
t = C - m o
s / Ö n
สมมติฐานแย้ง
|
เขตปฏิเสธ H0 |
1. H1 : m > m o
2. H1
:
m < m o 3. H1
:
m ¹ m o |
t > t1 - a : n-1 t < - t1 - a : n-1 ½ t ½ > t1
- a / 2 : n-1 |
ตัวอย่าง ผู้อำนวยการโรงเรียนแห่งหนึ่งคาดว่าปริมาณกระดาษที่ใช้ในการถ่ายเอกสารในโรงเรียนจะไม่ต่ำกว่า 880 แผ่นต่อวัน
จึงเก็บข้อมูลปริมาณกระดาษที่ใช้ถ่ายเอกสารต่อวันมา 50 วัน
คำนวณได้ปริมาณเฉลี่ย 871 แผ่นต่อวัน
ค่าเบี่ยงเบนมาตรฐานเป็น 21 แผ่น
การคาดคะเนของผู้อำนวยการโรงเรียนถูกต้องหรือไม่ที่ระดับนัยสำคัญ 0.05
H0 : m ³ 880
H1 :
m < 880
สถิติที่ใช้
![]() Z = C - m o
Z = C - m o
s / Ö n
= 871-
880
![]() 21 / Ö50
21 / Ö50
=
- 3.03
การตัดสินใจ
จะปฏิเสธ H0 ถ้า Z ที่คำนวณได้ น้อยกว่า -1.67
สรุปผล
ค่า Z ที่คำนวณได้
น้อยกว่า -1.67 จึงปฏิเสธ H0 นั่นคือ การคาดคะเนของผู้อำนวยการโรงเรียนไม่ถูกต้อง
ซึ่งหมายความว่าโรงเรียนแห่งนี้ใช้กระดาษเพื่อถ่ายเอกสาร น้อยกว่า 880 แผ่นต่อวันอย่างมีนัยสำคัญทางสถิติที่ระดับ 0.05
แบบฝึก ผู้ผลิตไอศครีมรายหนึ่งเชื่อว่าไอศครีมของเขาประกอบด้วยแคลอรี่เฉลี่ย
500 แคลอรี่ต่อไอศครีมหนัก 1
กรัม เขาจึงสุ่มไอศครีมหนักก้อนละ 1 กรัมมา 25
ก้อน คำนวณปริมาณแคลอรี่เฉลี่ยได้ 510 แคลอรี่ต่อกรัม
และค่าเบี่ยงเบนมาตรฐานเป็น 23 แคลอรี่
อยากทราบว่าสิ่งที่ผู้ผลิตเชื่อจริงหรือไม่ ที่ระดับนัยสำคัญ .10
ถ้าปริมาณแคลอรี่ในไอศครีมหนัก 1
กรัมมีการแจกแจงใกล้เคียงกับการแจกแจงแบบปกติ
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………….
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
แบบฝึก ถ้าเชื่อกันว่านักศึกษาหญิงที่มีอายุ 17 – 22 ปี
ในปี 2538
จะมีความสูงเฉลี่ยมากกว่า ความสูงเฉลี่ยของนักศึกษาที่มีอายุ 17 –
22 ปีในปี 2530
และทราบว่าความสูงของนักศึกษาหญิงมีการแจกแจงแบบปกติ ส่วนความสูงเฉลี่ยของนักศึกษาหญิงปี 2530
เป็น 64.3 นิ้ว ค่าเบี่ยงเบนมาตรฐานเป็น 2.1 นิ้ว จึงสุ่มนักศึกษาหญิง (
ปี 2538 ) ที่มีอายุในช่วง 17 – 22 ปี จำนวน 33 คน
วัดความสูงและคำนวณได้ความสูงเฉลี่ยเป็น 65.4 นิ้ว จงทดสอบความเชื่อข้างต้นที่ระดับนัยสำคัญ 0.01 ถ้าค่าเบี่ยงเบนมาตรฐานของความสูงของนักศึกษาหญิงในปี 2538 เท่ากับของปี 2530
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
2. การทดสอบสมมติฐานเกี่ยวกับค่าสัดส่วนประชากร
(p )

![]() Z = p - p0
Z = p - p0
Ö p0 q0 / n
แบบฝึก บริษัทขายเครื่องสำอางยี่ห้อ PS คาดว่าผู้หญิงไทยใช้เครื่องสำอางยี่ห้อ PS อย่างน้อย 20
% จึงสุ่มตัวอย่างผู้ลิตไทยมา 500 คน
ปรากฏว่ามีผู้ใช้ระบุว่าใช้เครื่องสำอางยี่ห้อ PS 95 คน
อยากทราบว่าสิ่งที่บริษัทคาดไว้เป็นจริงหรือไม่ที่ระดับนัยสำคัญ .10
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
แบบฝึก
ถ้าสมาคมต่อต้านการสูบบุหรี่คาดว่าผู้ที่สูบบุหรี่จะเป็นผู้หญิง 15 %
จึงสุ่มตัวอย่างผู้สูบบุหรี่มา 200 คน
พบว่าเป็นผู้หญิง 21 คน
อยากทราบว่าสิ่งที่สมาคมต่อต้านการสูบบุหรี่เชื่อเป็นจริงหรือไม่ ถ้าให้ระดับนัยสำคัญ = .05
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
3. การทดสอบสมมติฐานเกี่ยวกับค่าแปรปรวนประชากร
(s 2 )
 c2 = ( n – 1
) S2
c2 = ( n – 1
) S2
s20
แบบฝึก ฟาร์มแห่งหนึ่งผลิตนมสดออกจำหน่ายโดยใส่ขวด ๆ ละ 1 ลิตร
และจากการตรวจสอบมักจะพบว่าปริมาณนมสดมักจะไม่เท่ากับ 1 ลิตร เจ้าของฟาร์มเชื่อว่าปริมาณนมในขวด 1
ลิตร จะมีค่าเบี่ยงเบนมาตรฐาน .1 ลิตร
ถ้าต้องการทดสอบความเชื่อดังกล่าวจึงสุ่มตัวอย่างมา 28 ขวด คำนวณค่าเบี่ยงเบนมาตรฐานได้ .13 ลิตร กำหนด a = .05 ถ้าปริมาณนมสดในขวดขนาด 1 ลิตร มีการแจกแจงแบบปกติ
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
4. การทดสอบสมมติฐานเกี่ยวกับผลต่างระหว่างค่าเฉลี่ยของสอง
ประชากร ( m 1 - m2 )
|
|
ค่าเฉลี่ย
|
ค่าแปรปรวน
|
|
ประชากรที่ 1 ประชากรที่ 2 |
m 1
m2 |
s21 s22 |
|
|
ขนาดตัวอย่าง
|
ค่าเฉลี่ย
|
ค่าแปรปรวน
|
|
ตัวอย่างที่สุ่มจากประชากรที่ 1 ตัวอย่างที่สุ่มจากประชากรที่ 2 |
n1
n2 |
C1
C2 |
S21 S22 |
1. การทดสอบแบบทางเดียว
H0 : m1 - m2 £ d0
หรือ
H0 : m1 - m2 ³
d0
H1 : m1 - m2 > d0
H1 : m1 - m2 < d0
2. การทดสอบแบบ 2 ทาง
H0 : m1 - m2 =
0
ถ้า d0 = 0 หรือ
H0 : m1 = m2
H1 : m1 - m2 ¹ 0
H1 : m1 ¹ m2
สถิติที่ใช้ทดสอบ
สามารถใช้สถิติ Z – test และ
t – test ขึ้นอยู่กับข้อตกลงเบื้องต้นของการใช้สถิติแต่ละตัว
4.1
การทดสอบความแตกต่างระหว่างค่าเฉลี่ยสองประชากร โดยใช้ Z – test
ข้อตกลงเบื้องต้นของ Z – test
1. กลุ่มตัวอย่างทั้ง 2 เป็นอิสระต่อกัน
2. ค่าของตัวแปรตามในแต่ละหน่วยเป็นอิสระกัน
3. กลุ่มตัวอย่างได้มาอย่างสุ่มจากประชากรที่มีการแจกแจงแบบปกติและมีขนาดใหญ่(>30)
4. ทราบค่าความแปรปรวนของแต่ละประชากร
H0 : m1 - m2 = d0 ถ้า d0 = ค่าคงที่ หรือ H0 : m1 = m2



 สถิติทดสอบ
Z =
(X1-X2)- d0
สถิติทดสอบ
Z =
(X1-X2)- d0
![]() Ö s12/ n1+s22/n2
Ö s12/ n1+s22/n2
ถ้าไม่ทราบค่า s12 และ s22 แทนค่าด้วย S12 และ S22
4.2
การทดสอบความแตกต่างระหว่างค่าเฉลี่ยสองประชากร โดยใช้ t – test ( Independent )
ข้อตกลงเบื้องต้นของ t – test (
Independent )
1. กลุ่มตัวอย่างทั้ง 2 เป็นอิสระต่อกัน
2. ค่าของตัวแปรตามในแต่ละหน่วยเป็นอิสระกัน
3. กลุ่มตัวอย่างได้มาอย่างสุ่มจากประชากรที่มีการแจกแจงแบบปกติหรือใกล้เคียงและมีขนาดเล็ก
4. ไม่ทราบค่าความแปรปรวนของแต่ละประชากร
H0 : m1 - m2 = d0 ถ้า d0 = ค่าคงที่ หรือ H0 : m1 = m2
มี 2 เงื่อนไข คือ ในกรณีที่ s12= s22
กับ
ในกรณีที่ s12 ¹ s22
สูตรสถิติทดสอบ ในกรณีที่ s12 = s22


 t = (X1 - X2) - d0
ในกรณีที่ s12= s22
t = (X1 - X2) - d0
ในกรณีที่ s12= s22
![]() SpÖ1/n1+1/n2
SpÖ1/n1+1/n2
โดยที่
Sp = ( n1-1) S12+
( n2-1) S22
n1+n2-2
ที่องศาอิสระ
n1+n2-2
สูตรสถิติทดสอบ ในกรณีที่ s12 ¹ s22



 t = (X1-X2)-
d0
ในกรณีที่ s12 ¹ s22
t = (X1-X2)-
d0
ในกรณีที่ s12 ¹ s22
![]() ÖS12/ n1+ S22/n2
ÖS12/ n1+ S22/n2
ที่องศาอิสระ
(S12/
n1+ S22/n2)2
![]() (S12/ n1)2+ (S22/n2)2
(S12/ n1)2+ (S22/n2)2
n1-1 n2- 2
ตัวอย่าง จากการที่มีนิสิตร้องเรียนอาจารย์ผู้สอนวิชาสถิติว่าการอนุญาตให้ใช้เครื่องคิดเลขในการสอบจะทำให้เกิดการได้เปรียบเสียเปรียบของคะแนนสอบเกินกว่า
15 % เนื่องจากความแตกต่างกันของเครื่องคิดเลข
อาจารย์ผู้สอนจึงต้องการทดสอบข้อร้องเรียนของนิสิต โดยการสุ่มตัวอย่างนิสิตมา 45 คน แล้วแบ่งนิสิตออกเป็น 2 กลุ่มอย่างสุ่ม กลุ่มที่ 1
มีนิสิต 23 คน ให้สอบโดยใช้เครื่องคิดเลข กลุ่มที่ 2 มีนิสิต 22
คน ให้สอบข้อเดียวกันโดยไม่ให้ใช้เครื่องคิดเลข
โดยที่ข้อสอบนั้นเป็นข้อสอบที่มีการคำนวณมาก ปรากฎว่าได้ข้อมูลดังนี้
|
|
คะแนนเฉลี่ย
|
ค่าความแปรปรวน |
ขนาดตัวอย่าง
|
|
ใช้เครื่องคิดเลข |
80.7
|
49.5 |
23 |
|
ไม่ใช้เครื่องคิดเลข |
78.9
|
60.4 |
22 |
จากข้อมูลที่ได้
จงทดสอบว่าคะแนนเฉลี่ยของกลุ่มที่ใช้เครื่องคิดเลขจะมากกว่าคะแนนเฉลี่ยของกลุ่มที่ไม่ใช้เครื่องคิดเลขไม่เกิน
15 % ( 15 คะแนน ข้อสอบคะแนนเต็ม 100 ) กำหนดระดับนัยสำคัญ = .10 และทราบว่าคะแนนสอบของทั้ง 2
กลุ่มมีการแจกแจงแบบปกติ
ที่มีค่าแปรปรวนเท่า กัน
H0 : m1 - m2 ≤ 15
H1 : m1 - m2 > 15
สถิติที่ใช้


 t = (X1
- X2) - d0
t = (X1
- X2) - d0
![]() SpÖ1/n1+1/n2
SpÖ1/n1+1/n2
โดยที่
Sp =
( n1-1) S12+ ( n2-1)
S22
ที่องศาอิสระ n1+n2-2
n1+n2-2
= (23-1)49.5 + (22-1)60.4
23+22-2
=
1089+1268.4
43
=
54.82
![]() t
=
80.7 - 78.9 –15
t
=
80.7 - 78.9 –15
![]() 54.82Ö1/23+1/22
54.82Ö1/23+1/22
=
-13.2
= -0.80
![]() 54.8250.297
54.8250.297
การตัดสินใจ จะปฏิเสธ H0 ถ้า t ที่คำนวณได้ มากกว่า t 43 (.90) =
1.303
สรุปผล
ค่า t ที่คำนวณได้น้อยกว่า 1.303 จึงคงสมมติฐาน H0 นั่นคือ
คะแนนเฉลี่ยของกลุ่มที่ใช้เครื่องคิดเลขจะมากกว่าคะแนนเฉลี่ยของกลุ่มที่ไม่ใช้เครื่องคิดเลขไม่เกิน
15 % อย่างมีนัยสำคัญทางสถิติที่ระดับ 0.10
|
แบบฝึก ครูในโรงเรียนแห่งหนึ่งต้องการทราบว่าการสอนแบบการสร้างผังความคิดจะเพิ่มคะแนนเฉลี่ยวิชาชีววิทยาของนักเรียนหรือไม่
จึงเก็บข้อมูลคะแนนสอบวิชาชีววิทยาของนักเรียน 2 ห้องโดยห้องแรกเรียนตามปกติ มีนักเรียน50 คน ห้องที่สองเรียนแบบการสร้างผังความคิดมีนักเรียน 30 คนได้คะแนนเฉลี่ยของนักเรียนห้องแรก 12.55 คะแนน ห้องที่สอง 13.30
คะแนน ค่าเบี่ยงเบนมาตรฐานห้องแรก เป็น 2.15
คะแนน ห้องที่สอง 2.38 คะแนน
จากข้อมูลที่มีอยู่จะทำให้ครูสรุปได้หรือไม่ว่าการสอนแบบการสร้างผังความคิดทำให้คะแนนเฉลี่ยวิชาชีววิทยา
เพิ่มขึ้น โดยกำหนดให้ a = .05 ทั้ง 2 กลุ่มมีการแจกแจงแบบปกติ ที่มีค่าแปรปรวนไม่เท่ากัน |
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
4.3
การทดสอบความแตกต่างระหว่างค่าเฉลี่ยสองประชากร โดยใช้ Dependent or paired
t – test
ข้อตกลงเบื้องต้นของ t – test ( Dependent or
paired t – test )
1. ข้อมูล 2 ชุดได้มาจากกลุ่มตัวอย่างเดียวกัน
หรือมาจากกลุ่มตัวอย่าง 2 กลุ่มที่สัมพันธ์กัน
2. ค่าของตัวแปรตามในแต่ละหน่วยเป็นอิสระกัน
3.
กลุ่มตัวอย่างได้มาอย่างสุ่มจากประชากรที่มีการแจกแจงแบบปกติหรือใกล้เคียง
4. ไม่ทราบค่าความแปรปรวนของแต่ละประชากร
H0 : m1 - m2 = d0 ถ้า d0 = ค่าคงที่ หรือ H0 : md = d0
 สถิติทดสอบ
สถิติทดสอบ
 t =
d- d0
t =
d- d0
Sd / Ö n
di = x 1i –
x 2i
d = å di/ n , Sd2 =
å( di -
d ) 2/ ( n-1)
แบบฝึก ในการทดสอบคุณภาพของยางรถยนต์
2 ยี่ห้อ
คือ A และ B จึงสุ่มตัวอย่างยางรถยนต์มายี่ห้อละ
5 อัน แล้วใส่ยางรถยนต์ยี่ห้อละ 1
อันที่ล้อหลังของรถยนต์แต่ละคัน
ดังนั้นจึงต้องใช้รถยนต์ 5 คัน
แล้วให้รถยนต์ทุกคันวิ่งจนกว่ายางจะเสีย
โดยบันทึกระยะทางที่วิ่งได้ดังนี้
ระยะทางที่วิ่งได้ ( หน่วย : 10,000 กิโลเมตร )
รถยนต์คันที่
|
ยางรถยนต์ A |
ยางรถยนต์ B |
1
2 3 4 5 |
10.6 9.8 12.3 9.7 8.8 |
10.2 9.4 11.8 9.1 8.3 |
อยากทราบว่าคุณภาพของยางรถยนต์ทั้ง
2
ยี่ห้อนี้แตกต่างกันหรือไม่
กำหนดระดับนัยสำคัญ = .05
ถ้าอายุการใช้งานของยางรถยนต์มีการแจกแจงแบบปกติ
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
5. การทดสอบความแตกต่างระหว่างสัดส่วนสองประชากร(
โดยใช้ Z – test)
H0 : P1
- P2 = P0 ถ้า P0 = ค่าคงที่
 สถิติทดสอบ
Z =
( p1- p2) - p0
สถิติทดสอบ
Z =
( p1- p2) - p0
![]() Ö(p1q1/n1)+ (p2q2/n2)
Ö(p1q1/n1)+ (p2q2/n2)
การทดสอบความแตกต่างระหว่างค่าความแปรปรวนสองประชากร
H0
: s12= s22

สถิติทดสอบ
F = S12
![]() S22
S22
S12 >
S22 ที่องศาอิสระ n1 – 1 และ n2 –
2
แบบฝึก ผู้จัดการบริษัทขายเครื่องซักผ้ายี่ห้อ A เชื่อว่า เครื่องซักผ้ายี่ห้อ A มีสัดส่วนสินค้าเสียภายในระยะประกัน
ไม่เท่ากับสัดส่วนของเครื่องยี่ห้อ B จึงสุ่มเครื่องซักผ้ายี่ห้อ
A และ B ที่ขายให้ลูกค้าในปีที่แล้วจำนวน
100 เครื่องและ 120 เครื่อง
ตามลำดับ
พบว่าเครื่องซักผ้าตัวอย่างยี่ห้อ A และ B ที่เสียในระยะประกันมี 5 และ 9
เครื่อง ตามลำดับ จงทดสอบความเชื่อของผู้จัดการ
ที่ระดับนัยสำคัญ .10
ถ้าอายุการใช้งานของเครื่องซักผ้ามีการแจกแจงแบบปกติ
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
แบบฝึก ถ้าต้องการเปรียบเทียบผลการรักษาโรคมะเร็ง 2 วิธี
จึงสุ่มคนไข้ที่ได้รับการรักษามาวิธีละ
100 คน พิจารณาผลของการรักษาโดยการตรวจสอบอาการ (
เชื้อโรค ) ที่เกิดขึ้นอีก ในช่วง 2 ปีนับจากได้รับการรักษา ได้ข้อมูลดังนี้
วิธีรักษา
|
จำนวนคนไข้
|
จำนวนคนไข้ที่ไม่มีอาการของโรคใน 2 ปี |
1
2 |
100 100 |
78 87 |
จงทดสอบว่าการรักษาโรคมะเร็งวิธีที่ 2 ได้ผลดีกว่าวิธีที่ 1 อย่างน้อย 15 % กำหนดระดับนัยสำคัญ =
.10
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
แบบฝึก ถ้านักลงทุนเชื่อกันว่าหุ้นของบริษัท A มีความเสี่ยงมากกว่าหุ้น
B โดยที่ความเสี่ยงวัดด้วยราคาหุ้นที่แปรผันไปในแต่ละวัน จึงมีการทดสอบความเชื่อข้างต้น โดยสุ่มราคาหุ้น A มา
25 วันและราคาหุ้น
B มา 4วัน
คำนวณค่าเบี่ยงเบนมาตรฐานได้ SA = .76 SB = .46 กำหนดระดับนัยสำคัญ =
.05
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
แบบฝึก ถ้าต้องการเปรียบเทียบค่าแปรปรวนของ 2
ประชากรว่าเท่ากันหรือไม่
โดยที่ประชากรทั้ง 2 มีการแจกแจงแบบปกติ จึงสุ่มตัวอย่างจากประชากรทั้ง 2 อย่างเป็นอิสระกัน และได้ข้อมูลดังนี้
n1 =
8 n2 =
12 S1 =
4.85 S2 =
6.35
กำหนดระดับนัยสำคัญ = 0.10
วิธีทำ H0 :
……………………………………………………………………………………..
H1 : ……………………………………………………………………………………..
สถิติทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
บริเวณวิกฤต
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
สรุปผลการทดสอบ
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………
การทดสอบสมมติฐานโดยใช้โปรแกรม SPSS for Windows
การทดสอบสมมติฐานสามารถวิเคราะห์
โดยใช้โปรแกรม SPSS for Windows
มีวิธีการ
ดังนี้
1.
การทดสอบความแตกต่างระหว่างกลุ่ม
1) ประชากรกลุ่มเดียว ( ใช้สถิติ one sample t - test )
1.1 ใช้คำสั่ง
 Analyze
Analyze
Compare Means
จะได้หน้าจอดังรูปที่ 1
One
- Sample T Test ….
รูปที่ 1
One Sample T Test
เมื่อ click ตามรูปที่
1 แล้วเลือกตัวแปรที่ต้องการใส่ใน box ของ Test variable ใส่ค่าที่เป็นเกณฑ์ใน box ของ Test value ดังตัวอย่างรูปที่ 2
รูปที่ 2
Test Variables
1.2 เลือก Options จะได้หน้าจอดังรูปที่ 3
รูปที่ 3 One Sample T
Test :Option
![]()
![]() ใส่ confidence interval แล้วเลือก continue จะกลับไปหน้าจอเดิม รูปที่ 1 แล้วคลิก
OK จะได้ผลลัพธ์ในตารางที่ 1
ใส่ confidence interval แล้วเลือก continue จะกลับไปหน้าจอเดิม รูปที่ 1 แล้วคลิก
OK จะได้ผลลัพธ์ในตารางที่ 1
ตารางที่
1 ผลลัพธ์ของตัวอย่าง
One - Sample
Test
|
|
Test Value = 30,000 |
|||||
|
t |
Df |
Sig (2 –tailed ) |
Mean Difference |
95 %
Confidence Interval
of the Difference |
||
|
Lower |
Upper |
|||||
|
Income of respondent |
11.17 |
1399 |
.0001 |
11567.14 |
9536.69 |
13597.60 |
จากตารางที่ 1
ค่า t = 11.17 sig
( 2-tailed ) = .000
แสดงว่ารายได้ของผู้รับผิดชอบครอบครัวเฉลี่ยแตกต่างจาก 30,000 ( เป็นการทดสอบ 2 ทาง ) ถ้าทดสอบทางเดียวนำค่า
Sig หาร 2 จะได้ Sig =
.0001 / 2 = .00005 แสดงว่า
รายได้ของผู้รับผิดชอบครอบครัวเฉลี่ยสูงกว่า 30,000 บาทที่ระดับนัยสำคัญ .05
2) ประชาการสองกลุ่มที่เป็นอิสระกัน ( ใช้สถิติ Independent t –t est )
2.1 ใช้คำสั่ง
 Analyze
Analyze
Compare Means จะได้หน้าจอดังรูปที่ 4
Independent –Sample T Test…..
รูปที่ 4 Independent –Sample T Test
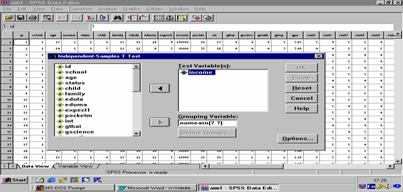
จากรูปที่ 4 เลือกตัวแปรที่ต้องการทดสอบใส่ในbox
ของTest
variable (s) เลือกตัวแปรต้นที่ใช้แบ่งตัวแปรตามเป็น2 กลุ่มใส่ใน box ของ Grouping variable ดังตัวอย่างในรูปที่
5
รูปที่ 5 Test variables
2.2 เลือก Define Group จะได้หน้าจอดังรูปที่ 6
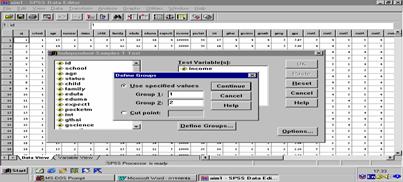
รูปที่ 6
Define Group
![]() ใส่ค่าของกลุ่มใน Group 1 และ Group 2 แล้วเลือก continue จะกลับมาที่หน้าจอเดิมรูป
5
ใส่ค่าของกลุ่มใน Group 1 และ Group 2 แล้วเลือก continue จะกลับมาที่หน้าจอเดิมรูป
5
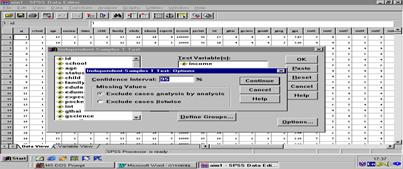
2.3 เลือก option จะได้หน้าจอ ดังรูปที่ 7
รูปที่ 7 Option
![]()
![]() เลือก confidence
Interval และ Missing values แล้วเลือก continue เพื่อกลับไปหน้าจอเดิม แล้วเลือก OK จะได้ผลลัพธ์ ในตารางที่ 2 และ
3
เลือก confidence
Interval และ Missing values แล้วเลือก continue เพื่อกลับไปหน้าจอเดิม แล้วเลือก OK จะได้ผลลัพธ์ ในตารางที่ 2 และ
3
ตารางที่ 2 Group Statistics
|
จำนวนผู้หาเลี้ยงครอบครัว |
N |
Mean |
Std. Deviation |
Std.Error Mean |
|
1 คน 2 คน |
513 887 |
30753.28 47821.39 |
35063.40 39383.34 |
1548.09 1322.36 |
ตารางที่ 3 Independent Sample Test
|
|
Levene’s Test for quality of Variances |
t –test
for Equality of Means |
|||||||
|
|
|
|
|
|
|
|
|
95% Confidence Interval of the Mean |
|
|
|
F |
Sig. |
T |
Df |
Sig (2-tailed) |
Mean Difference |
Sts.Error Difference |
Lower |
Upper |
|
Income Equal variances
assumed
Equal variances
not assumed |
11.773 |
.001 |
-8.128 -8.383 |
1398 1171.3 |
.000 .000 |
-17068.11 -17068.11 |
2099.94 2035.98 |
-21187.48 -21062.68 |
-12948.74 -13073.53 |
ความหมายของผลลัพธ์ในตารางที่
3
Levene’s Test for Equality of
Variance เป็นการทดสอบที่ใช้ในการทดสอบว่าค่าแปรปรวนประชากรจากแต่ละกลุ่มเท่ากันหรือไม่
เนื่องจากการศึกษานี้เป็นการสุ่มตัวอย่างผู้หาเลี้ยงครอบครัวจำนวน 1 คน มี 513
คนและผู้หาเลี้ยงครอบครัว จำนวน 2 คน มี 887 คน อย่างเป็นอิสระกัน (ขนาดตัวอย่างจากแต่ละกลุ่มไม่จำเป็นต้องเท่ากัน
) และไม่ทราบค่าแปรปรวนประชากรของรายได้ของแต่ละกลุ่ม จึงต้องตรวจสอบว่า
ค่าแปรปรวนประชากรของรายได้ของอย่างผู้หาเลี้ยงครอบครัวจำนวน 1 คน เท่ากับของผู้หาเลี้ยงครอบครัวจำนวน 2 คน หรือไม่
H0 : s 21 =
s 22
H1 : s 21 ¹ s 22
สถิติทดสอบ F
= 11.775
เขตปฏิเสธ จะปฏิเสธสมมติฐาน H0 ถ้า
1. F > F .975 : 1 ,
89
ซึ่งค่า F .975 :
1 , 89 จะเปิดได้จากตารางการแจกแจงแบบ F หรือ
2. ค่า Significance
< a
โดยที่ Significance =
P (F > F ที่คำนวณได้ )
ในที่นี้ P (F >
11.775 ) = Sig = .001
ซึ่งน้อยกว่าค่า a (.05) จึงปฏิเสธสมมติฐาน
H0 นั่นคือ
ค่าแปรปรวนของรายได้ของผู้หาเลี้ยงครอบครัวจำนวน 1 คน
ไม่เท่ากับของผู้หาเลี้ยงครอบครัวจำนวน 2 คน s 21 ¹ s 22
วัตถุประสงค์ของการทดสอบ t
– test ต้องการทราบว่ารายได้เฉลี่ยของครอบครัวจากผู้หาเลี้ยงครอบครัวจำนวน
1 คนมากกว่าของผู้หาเลี้ยงครอบครัวจำนวน 2 คนหรือไม่ โดยใช้ a = .05 สมมติฐานเพื่อการทดสอบคือ
H0
: รายได้เฉลี่ยของครอบครัวจากผู้หาเลี้ยงครอบครัวจำนวน
1 คนเท่ากับรายได้เฉลี่ยของครอบครัวจากผู้หาเลี้ยงครอบครัวจำนวน 2 คน
H1
: รายได้เฉลี่ยของครอบครัวจากผู้หาเลี้ยงครอบครัวจำนวน
2
คนมากกว่ารายได้เฉลี่ยของครอบครัวจากผู้หาเลี้ยงครอบครัวจำนวน 1 คน
จากตารางที่
3 ผลลัพธ์ของ t –test จะใช้ส่วนของ Equal variance not assumed เนื่องจาก Levene’ s Test สรุปได้ว่า s 21 ¹ s 22
t ในที่นี้ =
-8.383 sig (2-tailed ) =
.000 แต่เนื่องจากสมมติฐานเลือก เป็น 1-tailed ดังนั้น sig
(1-tailed ) = .000 / 2 = .000 แสดงว่า ปฏิเสธ H0 นั่นคือ: รายได้เฉลี่ยของครอบครัวจากผู้หาเลี้ยงครอบครัวจำนวน
2
คนมากกว่ารายได้เฉลี่ยของครอบครัวจากผู้หาเลี้ยงครอบครัวจำนวน 1
คนอย่างมีนัยสำคัญที่ระดับ 0.05
การนำเสนอผลการวิจัย ควรสร้างตารางนำเสนอใหม่
ซึ่งสามารถนำเสนอผลการวิเคราะห์ได้ในตารางต่อไปนี้
|
กลุ่ม |
เงินเดือน |
t – test |
p –value |
|
|
ค่าเฉลี่ย |
ส่วนเบี่ยงเบนมาตรฐาน |
|||
|
ผู้หาเลี้ยงครอบครัวจำนวน 1 คน ผู้หาเลี้ยงครอบครัวจำนวน 2 คน |
30753.28 47821.39 |
35063.40 39383.34 |
-8.383 |
.000 |
3)
ประชากรสองกลุ่มไม่เป็นอิสระกัน ( ใช้สถิติ dependent t-test )
3.1ใช้คำสั่ง
 Analyze
Analyze
Compare Means จะได้หน้าจอรูปดังรูปที่ 8 Paired
- Samples T Test….
รูปที่ 8 Paired –
SamplesT-Test
![]()
จากรูปที่ 8
เลือกตัวแปรที่จะทดสอบ โดยเลือกครั้งละ 1 ตัว
โดยตัวแปรแรกจะเข้าไปอยู่
variable 1 ตัวแปรตัวที่ 2 จะเข้าไปอยู่ variable 2 คลิกเลือกเครื่องหมาย 4 จะปรากฏตัวแปรทั้ง 2 ใน box ของ Paired variables ดังรูปที่ 9
รูปที่ 9 Paired – variables
![]() 3.2 เลือก
options……….
ใส่ confidence interval
3.2 เลือก
options……….
ใส่ confidence interval
![]()
![]() เลือก Exclude
analysis by analysis เลือก continue และเลือก OK จะได้ผลลัพธ์ในตารางที่
4-6
เลือก Exclude
analysis by analysis เลือก continue และเลือก OK จะได้ผลลัพธ์ในตารางที่
4-6
ตารางที่ 4 Paired Samples Statistics
|
|
Mean |
N |
Std. Deviation |
Std.Error Mean |
|
Pair 1 EDUFA
EDUMA |
12.05 10.91 |
1406 1406 |
4.81 5.17 |
.13 .14 |
จากตารางที่ 4
หมายความว่า
จำนวนปีของการศึกษาเฉลี่ยของบิดา ( mean ของ EDUFA ) = 12.05
ส่วนเบี่ยงมาตรฐานเท่ากับ 4.81
ส่วนจำนวนปีของการศึกษาเฉลี่ยของมารดา(mean ของ EDUMA) =10.91 ส่วนเบี่ยงมาตรฐานเท่ากับ (SD) =
5.17
ตารางที่ 5
Paired Sample correlation
|
|
N |
Correlation |
Sig. |
|
Pair 1 EDUFA & EDUMA |
1406 |
.716 |
.000 |
จากตารางที่ 5 หมายความว่า จำนวนปีของการศึกษาเฉลี่ยของบิดา
และมารดามีความสัมพันธ์กันในทิศทางบวก = 0.716 อย่างมีนัยสำคัญทางสถิติที่ระดับ 0.05
ตารางที่ 6 Paired
Samples Test
|
|
Paired
Differences |
t |
df |
Sig. (2-tailed) |
||||
|
Mean |
Std. Deviation |
Std.Error Mean |
95%
Confidence Interval of the Difference |
|||||
|
Lower |
Upper |
|||||||
|
Pair
1 EDUFA -
EDUMA |
1.14 |
3.78 |
.10 |
.94 |
1.33 |
11.29 |
1405 |
.000 |
จากตารางที่ 6
หมายความว่า
จำนวนปีของการศึกษาเฉลี่ยของบิดา
และมารดาแตกต่างกันอย่างมีนัยสำคัญที่ระดับ
0.05 ( t = 11.29 ,
sig = .000 )
การนำเสนอผลในการวิจัย
ไม่จำเป็นต้องนำตารางจากการวิเคราะห์ด้วย SPSS for
Windows ทุกตารางไปใส่
ควรสร้างตารางใหม่และนำค่าที่สำคัญไปนำเสนอ เช่น
การนำเสนอผลการวิเคราะห์ในเรื่องนี้
สามารถเสนอได้ ดังนี้
|
|
จำนวนปีของการศึกษา |
|
|
|
|
กลุ่ม |
ค่าเฉลี่ย |
ส่วนเบี่ยงเบนมาตรฐาน |
t - test |
p -value |
|
บิดา มารดา |
12.05 10.91 |
4.81 5.17 |
11.291 |
.000 |
การวิเคราะห์ความแปรปรวน ( Analysis of
Variance )
หลักการของการวิเคราะห์ความแปรปรวน
การวิเคราะห์ความแปรปรวน ใช้อักษรย่อที่เรารู้จักกันคือ ANOVA ซึ่งเป็นระเบียบวิธี(ไม่ใช่สถิติทดสอบ) ที่สามารถนำมาวิเคราะห์โดยมีหลักเกณฑ์ที่ใช้ในการทดสอบสมมติฐาน คือ
การแยกความแปรปรวนทั้งหมดของข้อมูลออกตามสาเหตุที่ทำให้ข้อมูลแตกต่างกัน
นั่นคือแยกความแปรปรวน/ ความผันแปรทั้งหมดของข้อมูลออกเป็น
1.
ความผันแปรระหว่างประชากร ( Sum of
Square Between Groups ( SSB ) )
2.
ความผันแปรภายในประชากรเดียวกัน ( Sum of Square Within Groups ( SSW ) )
ความผันแปรทั้งหมด = ความผันแปรระหว่างประชากร + ความผันแปรภายในประชากรเดียวกัน
Sum of
Square Total (SST)
= Sum of Square Between Groups+ Sum of Square
Within Groups
![]()
![]() Mean Squares Between Groups ( MSB ) = SSB =
SSB
Mean Squares Between Groups ( MSB ) = SSB =
SSB
![]()
![]() dfB
K- 1 Mean Squares Within Groups (
MSW)
= SSW
=
SSW
dfB
K- 1 Mean Squares Within Groups (
MSW)
= SSW
=
SSW
dfw
n - K
![]() สถิติทดสอบ
F = MSB
ซึ่งมีการแจกแจงแบบ F ด้วยองศาอิสระ
K – 1, n - K
สถิติทดสอบ
F = MSB
ซึ่งมีการแจกแจงแบบ F ด้วยองศาอิสระ
K – 1, n - K
MSW
ซึ่งเป็นอัตราส่วนระหว่างค่าผันแปรระหว่างประชากรกับค่าผันแปรภายในประชากร
โดยที่ K คือ
จำนวนกลุ่มประชากร
n คือ จำนวนหน่วยตัวอย่าง
ถ้าความผันแปรระหว่างประชากรมีค่ามากเมื่อเทียบกับความผันแปรภายในประชากรเดียวกัน
แสดงว่าความแตกต่างระหว่างค่าเฉลี่ยประชากรมากกว่าความแตกต่างภายในประชากรเดียวกัน
ในกรณีนี้จะปฏิเสธสมมติฐาน Ho ที่ค่าเฉลี่ยของประชากรเท่ากัน
นั่นคือจะสรุปได้ว่ามีค่าเฉลี่ยประชากรอย่างน้อย 1
ประชากรที่แตกต่างจากประชากรอื่นๆ
ความผันแปรภายในประชากรเดียวกันมีค่ามากกว่าความผันแปรระหว่างประชากร
จะทำให้สรุปได้ว่าค่าเฉลี่ยประชากรที่ต้องการทดสอบนั้นไม่แตกต่างกัน
ข้อตกลงเบื้องต้นของ การวิเคราะห์ความแปรปรวน
1. Independent : การสุ่มตัวอย่างแต่ละหน่วยจากแต่ละประชากรจะต้องเป็นอิสระจากกัน
2. Normality : ประชากรทั้ง Kกลุ่มมีการแจกแจงแบบโค้งปกติ
3.
Homogeneity of variances : ค่าความแปรปรวนของแต่ละประชากรมีค่าเท่ากัน
การวิเคราะห์ความแปรปรวน
ในที่นี้จะขอกล่าวถึง ONE
way ANOVA ( ตัวแปรอิสระ
1 ตัว )และ N - way ANOVA
( ตัวแปรอิสระ 2 ตัว ขึ้นไป )
ONE way
ANOVA เป็นการวิเคราะห์ความแปรปรวนที่มีตัวแปรอิสระ
1 ตัว ที่มีมาตรการวัดแบบนามบัญญัติหรืออันดับ
โดยแบ่งกลุ่มมากกว่า 2 กลุ่มตัวอย่าง ส่วนตัวแปรตามมี 1 ตัวโดยมีมาตรการวัดแบบอันตรภาคหรืออัตราส่วน
N
- way ANOVA เป็นการวิเคราะห์ความแปรปรวนที่มีตัวแปรอิสระ มากกว่า1 ตัว ที่มีมาตรการวัดแบบนามบัญญัติหรืออันดับ ส่วนตัวแปรตามมี 1 ตัวโดยมีมาตรการวัดแบบอันตรภาคหรืออัตราส่วน
การวิเคราะห์ความแปรปรวน
แบบ ONE way
ANOVA
|
สรุปการวิเคราะห์ความแปรปรวนแบบมีปัจจัยเดียว เพื่อทดสอบความแตกต่างระหว่าง ค่าเฉลี่ย
k ประชากร สมมติฐาน H0 : m1 = m2 = m3=… = mk
H1 : มี mi ¹ mj อย่างน้อย 1 คู่ ; i ¹ j สถิติทดสอบ F = MSTrt
MSE
เขตปฏิเสธ
จะปฏิเสธ H0 ถ้า
F > F
1-a;k-1,n-k |
ตารางการคำนวณของ ANOVA
|
แหล่งแปรปรวน |
องศาอิสระ
DF |
ผลบวกกำลัง สอง SS |
ค่าเฉลี่ยกำลังสอง MS = SS/DF |
F |
|
k-1
n-k |
SSTrt SSE |
MSTrt MSE |
MSTrt
MSE
|
|
ผลรวม ( Total ) |
n-1
|
SST |
|
|
ตัวอย่าง
เปรียบเทียบผลการประเมินการปฏิบัติของส่วนงาน 3 แห่ง
ตัวแปรอิสระ (X)
: ส่วนงาน 3 แห่ง
ตัวแปรตาม (Y) : คะแนนประเมินผล
![]()
![]()
![]() ส่วนงาน ก. ส่วนงาน ข. ส่วนงาน ค.
10 6 5
ส่วนงาน ก. ส่วนงาน ข. ส่วนงาน ค.
10 6 5
9 4 6
10 7 5
8 3 2
8 5 2
![]() รวม 45 25 20
รวม 45 25 20
![]() Ho : m 1 = m 2 = m3
Ho : m 1 = m 2 = m3
H1
: m i ¹ m j อย่างน้อย 1 คู่
ค่าสถิติที่ต้องหา
![]() 1
) ค่าความแตกต่างทั้งหมด ( The total variation ) คำนวณได้จากการเปรียบเทียบค่าจริงกับค่าเฉลี่ยทั้งหมด
( Grand mean ) Y
1
) ค่าความแตกต่างทั้งหมด ( The total variation ) คำนวณได้จากการเปรียบเทียบค่าจริงกับค่าเฉลี่ยทั้งหมด
( Grand mean ) Y
สูตร Sum of
Square Total ( SST )
n
![]() SST = å ( Yi - Y ) 2
SST = å ( Yi - Y ) 2
![]()
![]() i=1 2
) ค่าความแตกต่างระหว่างกลุ่ม ( The between group variation
) คำนวณได้จากการเปรียบเทียบค่าเฉลี่ยของแต่ละกลุ่ม(Yj)
กับค่าเฉลี่ยทั้งหมด (Y)
i=1 2
) ค่าความแตกต่างระหว่างกลุ่ม ( The between group variation
) คำนวณได้จากการเปรียบเทียบค่าเฉลี่ยของแต่ละกลุ่ม(Yj)
กับค่าเฉลี่ยทั้งหมด (Y)
สูตร Sum of
Square Between Groups ( SSB )
K
![]()
![]() SSB = å n ( Yj -Y ) 2
SSB = å n ( Yj -Y ) 2
j = 1
![]() 3
) ค่าความแตกต่างภายในกลุ่ม
( The within group
variation ) คำนวณได้โดยการเปรียบเทียบค่าจริงของหน่วยตัวอย่างที่เกิดขึ้นของแต่ละกลุ่ม(
Yi j)กับค่าเฉลี่ยของกลุ่มนั้น(Yj)
3
) ค่าความแตกต่างภายในกลุ่ม
( The within group
variation ) คำนวณได้โดยการเปรียบเทียบค่าจริงของหน่วยตัวอย่างที่เกิดขึ้นของแต่ละกลุ่ม(
Yi j)กับค่าเฉลี่ยของกลุ่มนั้น(Yj)
สูตร Sum
of Square Within Groups ( SSW )
K n
![]() SSW = å
å ( Yi j - Yj ) 2
SSW = å
å ( Yi j - Yj ) 2
j = 1 i=1
SST = SSB + SSW
![]()
![]() MST = SST
= SST
MST = SST
= SST
dfT
n - 1
![]()
![]() MSB = SSB
= SSB
MSB = SSB
= SSB
dfB
K - 1
![]()
![]() MSW = SSW
= SSW
MSW = SSW
= SSW
dfw
n – K
![]() F = MSB
F = MSB
MSW
![]() h2 = SSB
h2 = SSB
SST
แทนค่าจากตัวอย่าง
ค่าเฉลี่ยของแต่ละกลุ่ม
![]() y1
= 45 = 9
y1
= 45 = 9
5
![]() y2 = 25 = 5
y2 = 25 = 5
5
![]() y3 = 20 = 4
y3 = 20 = 4
5
ค่าเฉลี่ยทั้งหมด ( Grand mean )
![]()
![]() y = 45+25+20 = 6
y = 45+25+20 = 6
15
ค่า Sum of
Square ทั้ง 3 สามารถคำนวณได้ ดังนี้
SST = ( 10 - 6 )2+ ( 9 - 6 )2+
( 10 - 6 )2 + ( 8 - 6 )2+( 8 - 6 )2 +( 6 - 6 )2+(
4 - 6 )2+ ( 7 - 6 )2+ ( 3 - 6 )2+ ( 5 - 6 )2+
( 5 - 6 )2+ ( 6 - 6 )2+ ( 5 - 6 )2+ ( 2 - 6 )2+
( 2 - 6 ) 2
= 98
SSB = 5 ( 9 - 6 ) 2 + 5 ( 5 -
6 ) 2 + 5 ( 4 - 6 ) 2
= 70
SSW = ( 10 - 9 )2 + ( 9 - 9 )2
+ ( 10 - 9 )2 + ( 8 - 9 )2 + ( 8 - 9 )2 + ( 6 - 5 )2 + ( 4 - 5)2
+
(7 - 5 )2+ ( 3 - 5 )2+ ( 5 - 5 )2+ ( 5
- 4 )2+ ( 6 - 4 )2+ ( 5 - 4 )2+ ( 2 - 4 )2+
(2 -4 )2
= 28
F = MSB
![]() MSW
MSW
![]() = SSB
/ ( K - 1 )
= SSB
/ ( K - 1 )
SSW
/ ( n - K )
= 70
/ ( 3 - 1 )
![]() 28
/ ( 15 - 3 )
28
/ ( 15 - 3 )
= 70 x 12 = 15.02
2 28
ผลการวิเคราะห์ความแปรปรวนทางเดียว
|
แหล่งความแปรปรวน |
df |
SS |
MS |
F |
|
ระหว่างกลุ่ม ภายในกลุ่ม รวม |
2 12 14 |
70 28 98 |
35 2.33 |
15.02 |
เปิดตาราง Critical value ของ F จากตาราง µ = 0.01 และ องศาอิสระของ F คือ
2 และ 12 คือ 6.93
![]() F คำนวณ > F เปิดตาราง
ปฏิเสธ Ho
สรุปได้ว่าคะแนนประเมินผลเฉลี่ยของ
ส่วนงานมีความแตกต่างกันอย่างน้อย 1 คู่
อย่างมีนัยสำคัญทางสถิติที่ระดับ 0.01
F คำนวณ > F เปิดตาราง
ปฏิเสธ Ho
สรุปได้ว่าคะแนนประเมินผลเฉลี่ยของ
ส่วนงานมีความแตกต่างกันอย่างน้อย 1 คู่
อย่างมีนัยสำคัญทางสถิติที่ระดับ 0.01
การที่จะทราบว่ากลุ่มใดบ้างที่แตกต่างกัน
ต้องทำการทดสอบต่อไป เรียกว่า Post hoc analysis โดยใช้วิธีการวิเคราะห์ที่เรียกว่าวิธีเปรียบเทียบพหุ
(Multiple comparison procedure) ซึ่งมีหลายวิธี
ดังต่อไปนี้
วิธีการเปรียบเทียบซึ่งโปรแกรม
SPSS แบ่งออกเป็น 2 กลุ่มคือ
1.
วิธีการเปรียบเทียบเชิงซ้อนที่มีเงื่อนไขว่า
ค่าแปรปรวนของข้อมูลทุกชุดต้องเท่ากัน ประกอบด้วย
1.Least-Significant Different(LSD)
2.Bonferroni
3.Sidak
4.Scheffe
5.RE-G-WF
6.R-E-G-WQ
7.S-N-K(Student-Newman-Keuls)
8.Tukey
9.Tukey’s – b
10.Duncan
11.Hochberg’s GT2
12.Gabriel
13.Waller – Duncan
14.Dunnett’s C
2.
วิธีการเปรียบเทียบเชิงซ้อนที่ไม่มีเงื่อนไขเกี่ยวกับการเท่ากันของค่าแปรปรวน
1.Tamhane’s
T2
2.Dunnett’s
T3
3.Games-Howell
4.Dunnett’s
C
ในที่นี้จะอธิบายวิธีการเปรียบเทียบเชิงซ้อนบางวิธีดังนี้
1.
Least-Significant
Different(LSD)
LSD หรือ Fisher’s Least-Significant
Difference เป็นเทคนิคที่ R.A. Fisher ได้
พัฒนาขึ้นเพื่อเปรียบเทียบค่าเฉลี่ยประชากรได้ครั้งละหลายคู่ โดยมีขั้นตอนดังนี้
1.
คำนวณค่า LSD โดยที่
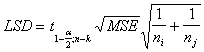
ถ้า ni = nj จะทำให้
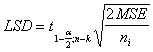
คำนวณความแตกต่างระหว่างค่าเฉลี่ย ![]()
2. นำ ![]() เปรียบเทียบกับค่า
LSD
เปรียบเทียบกับค่า
LSD
3.1 ถ้า ![]() > LSD
แสดงว่า
> LSD
แสดงว่า ![]()
3.2 ถ้า ![]() £ LSD แสดงว่า
£ LSD แสดงว่า ![]() ไม่แตกต่างจาก
ไม่แตกต่างจาก ![]()
หมายเหตุ ส่วนใหญ่ผู้วิเคราะห์มักจะคำนวณหา ![]() แล้วนำมาเปรียบเทียบกับค่า LSD
แล้วนำมาเปรียบเทียบกับค่า LSD
2.
Student-Newman-Keuls
(SNK) Multiple Range Test
เป็นวิธีการเปรียบเทียบค่าเฉลี่ยประชากรโดยใช้ค่าเฉลี่ยตัวอย่างมีค่ามากที่สุดและน้อย
ที่สุดกับค่า Studentized range statistic
เงื่อนไข วิธีนี้จะใช้ได้เมื่อขนาดตัวอย่างแต่ละชุดเท่ากัน
คือ ![]()
![]()
โดยที่ค่า q
เปิดได้จากตาราง และ v = จำนวนค่าเฉลี่ยที่อยู่ในช่วงที่เปรียบเทียบ
โดยพิจารณาจากค่าเฉลี่ยตัวอย่างแต่ละชุดที่เรียงลำดับจากน้อยไปมาก จำนวน t ค่าดังนี้
![]()
![]()
![]()
![]()
ขั้นตอนในการใช้ SNK ในการเปรียบเทียบค่าเฉลี่ย 2 ประชากรหลาย ๆ คู่พร้อมกัน มีดังนี้
1.
คำนวณค่า SNK
2.
คำนวณค่าเฉลี่ยตัวอย่าง ![]() แล้วนำมาเรียงลำดับจากน้อยไปหามาก
แล้วนำมาเรียงลำดับจากน้อยไปหามาก
3. คำนวณค่า ![]()
4.
นำค่า ![]() เปรียบเทียบกับ SNK(v,a)
เปรียบเทียบกับ SNK(v,a)
4.1 ถ้า ![]() > SNK(v,a) จะปฏิเสธ H0 นั่นคือ
> SNK(v,a) จะปฏิเสธ H0 นั่นคือ ![]() โดยที่
โดยที่ ![]() และ
และ
![]() ห่างกัน v อันดับ
ห่างกัน v อันดับ
4.2 ถ้า ![]() £ SNK(v,a)
จะสรุปว่า
£ SNK(v,a)
จะสรุปว่า ![]() ไม่แตกต่างจาก
ไม่แตกต่างจาก ![]()
3.Tukey’s Honesty Significant Difference (HSD)
เป็นวิธีการเปรียบเทียบค่าเฉลี่ยประชากร ที่มีเงื่อนไขเหมือนวิธี SNK คือ ตัวอย่างแต่ละชุดมีขนาดเท่ากัน = r
![]()
โดยที่ v
= จำนวนกลุ่ม/ประชากรที่ต้องการเปรียบเทียบ ค่า q เปิดได้จากตาราง ขั้นตอนมีดังนี้
1.
คำนวณ HSD
2.
คำนวณค่า ![]()
3.
เปรียบเทียบค่า ![]() กับ HSD
กับ HSD
3.1 ถ้า ![]() > HSD แสดงว่า
> HSD แสดงว่า ![]()
3.2 ถ้า ![]() £ HSD จะสรุปว่า
£ HSD จะสรุปว่า ![]() ไม่แตกต่างจาก
ไม่แตกต่างจาก ![]()
หมายเหตุ
สำหรับวิธีอื่น ๆ คือ Duncan ,
Tukey’s และ Scheffe มีหลักเกณฑ์คล้าย ๆ
กัน โดยที่ Scheffe จะใช้สถิติ F
การวิเคราะห์ความแปรปรวน
แบบ N- way ANOVA
ในที่นี้จะขอยกตัวอย่าง Two-
way ANOVA
ตัวอย่างเช่น ผลการเรียนซึ่งขึ้นอยู่กับปัจจัย 2 ปัจจัยคือ
ปัจจัยที่ 1 : ครูผู้สอนซึ่งมี 3 คน ( a = 3 )
ปัจจัยที่ 2 : วิธีการสอนซึ่งมี 4 วิธี ( b = 4 )
ซึ่งทำให้มีจำนวนทรีทเม้นต์
= ab 3(4) = 12
ทรีทเม้นต์ โดยที่ทรีทเม้นต์ที่ 1 คือ ครูผู้สอนคนที่ 1 ใช้วิธีการสอนแบบที่ 1
,….., และทรีทเม้นต์ที่ 12 คือ ครูผู้สอนคนที่
3 ใช้วิธีการสอนแบบที่ 4
และ m คือจำนวนข้อมูลในแต่ละทรีทเม้นต์
สำหรับเงื่อนไขของการวิเคราะห์ความแปรปรวนแบบมี 2
ปัจจัย มีดังนี้
1.
แต่ละประชากรมีการแจกแจงแบบปกติ
2.
แต่ละประชากรมีค่าแปรปรวนเท่ากัน
SST = SSA + SSB + SSAB + SSE
SST = ผลบวกของความผันแปรทั้งหมดที่มีองศาอิสระ
abm – 1
= n-1
SSA = ผลบวกของความผันแปรที่เกิดจากปัจจัย A ที่มีองศาอิสระ (
a-1 )
SSB = ผลบวกของความผันแปรที่เกิดจากปัจจัย B ที่มีองศาอิสระ (
b-1 )
SSAB = ผลบวกของความผันแปรที่เกิดจากอิทธิพลร่วมของปัจจัย
A และ B ที่มีองศา
อิสระ(
a-1 ) ( b-1 )
SSE = ผลบวกของความคลาดเคลื่อนยกกำลังสอง ที่มีองศาอิสระ ab(m-1)
![]()
![]()
![]()
![]()
![]() SST = SSS( Ci j k - X
) 2
SST = SSS( Ci j k - X
) 2
a
![]() SSA = S bm ( Ai - X ) 2
SSA = S bm ( Ai - X ) 2
i=1
b
![]() SSB = S bm ( Bj - X ) 2
SSB = S bm ( Bj - X ) 2
j=1
SSE = SSS( Ci j k
- ( AB )i j ) 2
และ SSAB = SST – SSA – SSB – SSE
ตารางการวิเคราะห์ความแปรปรวนแบบมี
2 ปัจจัย
|
F |
องศาอิสระ |
SS |
MS
= SS/df |
F |
|
ปัจจัย A ปัจจัย B AB ความคลาดเคลื่อน |
a-1 b-1 (a-1)(b-1) ab(m-1) |
SSA SSB SSAB SSE |
MSA MSB MSAB MSE |
MSA/ MSE MSB/ MSE
MSAB/
MSE |
|
ผลรวม |
abm-1 |
SST |
|
|
สมมติฐานของการทดสอบเมื่อมีปัจจัย 2 ปัจจัย มีดังนี้
1. การทดสอบอิทธิพลของระดับต่าง
ๆ ของปัจจัยที่ 1 ( ปัจจัย A )
H0 : ไม่มีความแตกต่างระหว่างระดับต่าง
ๆ ของปัจจัย A ( ปัจจัยที่ 1 )
H1 : มีอย่างน้อย 1 ระดับที่แตกต่างจากระดับอื่น ๆ ของปัจจัย A
สถิติทดสอบ F = MSA
MSE
เขตปฏิเสธ จะปฏิเสธ H0 ถ้า F > F1- a ; ที่องศาอิสระ ( a-1) และ ab(m-1)
2. การทดสอบอิทธิพลของระดับต่าง
ๆ ของปัจจัยที่ 2 ( ปัจจัย B )
H0 : ไม่มีความแตกต่างระหว่างระดับต่าง
ๆ ของปัจจัย B ( ปัจจัยที่ 2 )
H1 : มีอย่างน้อย
1 ระดับที่แตกต่างจากระดับอื่น ๆ ของปัจจัย B
สถิติทดสอบ F = MSB
MSE
เขตปฏิเสธ จะปฏิเสธ H0 ถ้า F > F1- a ; ที่องศาอิสระ ( b-1) และ ab(m-1)
3. การทดสอบอิทธิพลของระดับต่าง
ๆ ของปัจจัยที่ 1 และ ปัจจัยที่ 2
H0 : ไม่มีความแตกต่างระหว่างระดับต่าง
ๆ ของปัจจัย A และ B
H1 : มีอย่างน้อย 1 ระดับที่แตกต่างจากระดับอื่น ๆ ของปัจจัย A และB
ที่ต่างจากทรีทเม้นต์อื่นๆ
สถิติทดสอบ F = MSAB
MSE
เขตปฏิเสธ จะปฏิเสธ H0 ถ้า F > F1- a ; ที่องศาอิสระ ( a-1)(b-1) และ ab(m-1)
ตัวอย่าง
ระดับค่านิยมเกี่ยวกับการประหยัดของประชาชนจำแนกตามการศึกษาและอาชีพ
ตัวแปรอิสระ (X1)
: อาชีพ 3 อย่าง
(X2) : การศึกษา 4 ระดับ
ตัวแปรตาม
(Y) :
ระดับค่านิยมเกี่ยวกับการประหยัดของประชาชน
![]()
![]() ข้าราชการ ค้าขาย เกษตรกร รวม
ข้าราชการ ค้าขาย เกษตรกร รวม
![]()
![]() X1 X21
X1 X21
X1
X21
X1 X21
X1 X21
X1
X21
![]() 2
4
3
9 4
16
2
4
3
9 4
16
3
9
4
16 3
9
ป 4 1
1
2 4 4 16
4
16
3 9 2
4
![]()
![]() รวม
10
30
12
38
13
45
35
รวม
10
30
12
38
13
45
35
5
25 4 16 5 25
4
16
3
9 2
4
จบมัธยมตอนต้น
3
9 2
4 3
9
![]() 2
4
1
1 3
9
2
4
1
1 3
9
![]() รวม
14
54
10
30
13
47
37
3 9 3 9 4 16
รวม
14
54
10
30
13
47
37
3 9 3 9 4 16
2 4 4 16 3
9
จบมัธยมตอนปลาย
3 9 4
16 5 25
![]() 1 1 3 9 3
9
1 1 3 9 3
9
รวม
9
23
14
50
15
59
38
![]() 3 9 4 16 5 25
3 9 4 16 5 25
2 4 4 16 3
9
จบอุดมศึกษา
4
16 1
1 3
9
![]() 1 1 4 16 4 16
1 1 4 16 4 16
![]()
![]() รวม
10
30
12
42
14
54
36 รวมทั้งหมด
43
137
48 160
55
205
146
รวม
10
30
12
42
14
54
36 รวมทั้งหมด
43
137
48 160
55
205
146
การคำนวณ ANOVA สองทางก็คล้ายกับทางเดียว
SST = SSx1 + SS x2 + SSx1
x2 + SS error
h2 = SSx1 + SS x2 + SSx1
x2
จากตัวอย่าง จะต้องหาค่า å X t , å X2
t และ nt ดังนี้
å X
t = 43
+ 48 + 55 =
146
å X2
t = 137
+ 160 + 206 = 502
nt = 16
+ 16 + 16
= 48
จากนั้นหาผลรวมความเบี่ยงเบนกำลังสอง
ซึ่งการวิเคราะห์แบบสองทางจะต้องหาร SS รวม ( SSt ) ตามแนวตั้ง ( SSc) ตามแนวนอน ( SSr
) ระหว่างกลุ่ม (
SSb ) ปฏิสัมพันธ์ร่วม
( SSi )และความคลาดเคลื่อน ( SSe
)
![]() SSt = å X2 t - ( å X t ) 2
SSt = å X2 t - ( å X t ) 2
nt
= 502 - ( 146 ) 2 = 57.92
![]() 48
48
![]() SSc = ( å Xc 1 ) 2 + ( å Xc 2 ) 2 +
( å
Xc 3 ) 2 - ( å Xt
) 2
SSc = ( å Xc 1 ) 2 + ( å Xc 2 ) 2 +
( å
Xc 3 ) 2 - ( å Xt
) 2
![]()
![]()
![]() nc1 nc2
nc3
nct
nc1 nc2
nc3
nct
= ( 43 ) 2 + ( 48 ) 2 + ( 55 ) 2
- ( 146 ) 2
![]()
![]()
![]()
![]() 16 16 16
48
16 16 16
48
= 4.54
SSr = ( å Xr 1 ) 2 + ( å Xr 2 ) 2 +
( å
Xr 3 ) 2 + ( å Xr4 - (å Xt ) 2
![]()
![]()
![]()
![]()
![]() nr1
nr2
nr3
nr4
nt
nr1
nr2
nr3
nr4
nt
![]()
![]()
![]()
![]()
![]() = ( 35 ) 2 + ( 37 ) 2 + ( 38 ) 2
+ ( 36 ) 2 - ( 146 ) 2
= ( 35 ) 2 + ( 37 ) 2 + ( 38 ) 2
+ ( 36 ) 2 - ( 146 ) 2
12 12
12
12
48
= 0.42
![]()
![]() SSb = ( å Xc 1r1 ) 2 + ( å Xc 2r2 ) 2 ++ ......... - ( å Xt ) 2
SSb = ( å Xc 1r1 ) 2 + ( å Xc 2r2 ) 2 ++ ......... - ( å Xt ) 2
![]() nc1r1
nc2r2
nt
nc1r1
nc2r2
nt
![]()
![]()
![]()
![]()
![]() = ( 10 ) 2 + ( 12 ) 2
+ ( 13 ) 2 ++...+ ( 14 ) 2 - ( 146 ) 2
= ( 10 ) 2 + ( 12 ) 2
+ ( 13 ) 2 ++...+ ( 14 ) 2 - ( 146 ) 2
4
4
4
4
48
= 10.92
SSi =
SSb - SSc -
SSr
= 10.92 - 4.54 - 0.42 = 5.96
SSe = SSt - SSb
= 57.92 - 10.92 = 47.00
จากนั้นทำตารางวิเคราะห์ความแปรปรวน
ดังนี้
![]() ผลการวิเคราะห์ความแปรปรวนสองทาง
ผลการวิเคราะห์ความแปรปรวนสองทาง
แหล่งความแปรปรวน df SS MS F P
![]()
ตามแนวตั้ง ( c
) 2 4.54 2.27 1.75
>
.05
ตามแนวนอน ( r ) 3 0.42 0.14 0.11
>
.05
ปฏิสัมพันธ์ร่วม ( i ) 6 5.96 0.99 0.76
>
.05
ความคลาดเคลื่อน ( e )
36
47.00 1.30 -
![]() รวม 47 57.92 - -
รวม 47 57.92 - -
ค่า df ของ SSe = c - 1 ของ SSr = r - 1 ของ SSi = ( c - 1 ) ( r - 1 ) และ SSe = nt - cr ของ SSt = nt - 1 ส่วน MS หาได้ด้วยการเอา df หาร SS ของแต่ละแหล่ง
F นั้น จะมีค่า 3 ค่าด้วยการเอา MSe หาร MSc
, Msr และ MSi
การแปลผลจะต้องดูค่า
F ของปฏิสัมพันธ์ร่วมก่อน
โดยนำไปเทียบกับ F ในตารางที่ df = 6,36 และ a = 0.05 มีค่า 2.42 แสดงว่าน้อยกว่าค่าในตาราง แปลว่า
อิทธิพลจากปฎิสัมพันธ์ระหว่างการศึกษากับอาชีพไม่มีผลต่อค่านิยมเกี่ยวกับการประหยัด
จากนั้นจึงแปลผลตามแนวตั้งและแนวนอนต่อไป เช่นเดียวกันคือ พบว่าน้อยกว่าค่า F
ในตาราง
แสดงว่าทั้งการศึกษาและอาชีพไม่มีผลที่จะทำให้ค่านิยมเรื่องนี้ต่างกัน
ถ้าต่างกันจะต้องวิเคราะห์รายคู่ต่อไปเช่นเดียวกับการวิเคราะห์ทางเดียว
ส่วนถ้าพบว่าปฏิสัมพันธ์ร่วมมีนัยสำคัญ ( Significance ) จะแปลผลตามแนวตั้งและแนวนอนต่อไปไม่ได้
เพราะจะทำให้เข้าใจผิดได้
ดังนั้นจึงต้องควบคุมตัวแปรตามแนวนอนและแนวตั้งทีละตัวและวิเคราะห์ต่อไป
การวิเคราะห์ ANOVA โดยใช้โปรแกรม SPSS
for Windows
มีวิธีการ ดังนี้
1.
การทดสอบความแตกต่างระหว่างกลุ่มที่มีประชากรมากกว่าสองกลุ่ม
ตัวแปรอิสระ 1 ตัว ( ใช้สถิติ one way ANOVA)
1.1 ใช้คำสั่ง
 Analyze
Analyze
Compare Means
One-Way
Anova
จะได้หน้าจอดังรูปที่
1
รูปที่ 1 One way
ANOVA
จากรูป 1 - เลือกตัวแปรตามที่มีระดับการวัด interval ขึ้นไป ใส่ใน Dependent List เช่น รายได้ของครอบครัว(income)
-
เลือกตัวแปรต้นที่มีระดับการวัดเป็น Nominal หรือ
Ordinal ที่มีการแบ่งกลุ่มเพื่อเปรียบเทียบค่าเฉลี่ยระหว่างกลุ่ม เช่น ชื่อโรงเรียน
ทั้งนี้เพื่อคำนวณรายได้เฉลี่ยจำแนกตามโรงเรียน ใส่ใน Factor
![]() 1.2 เลือก Post Hoc… จะได้หน้าจอดังรูปที่
2
1.2 เลือก Post Hoc… จะได้หน้าจอดังรูปที่
2
รูปที่ 2 Post Hoc
Multiple Comparisons
จากรูปที่ 2
จะแสดงถึงวิธีการเปรียบเทียบเชิงซ้อน
เพื่อต้องการทดสอบว่าค่าเฉลี่ยของกลุ่มใดบ้างที่แตกต่างกัน ซึ่งมี 2 เงื่อนไข คือ
1. Equal
Variances Assumed หมายถึง ข้อมูลทุกชุดต้องมีค่าความแปรปรวนเท่ากัน จึงใช้สถิติทดสอบคู่ที่แตกต่างใน BOX
แรกรูป 8
ตัวใดตัวหนึ่งหรือหลายตัวก็ได้
2. ![]() Equal
Variances Not Assumed หมายถึง
ข้อมูลทุกชุดไม่มีเงื่อนไขของการเท่ากันเลือกสถิติทดสอบแล้วเลือก continue จะกลับมาที่หน้าจอรูป
1
Equal
Variances Not Assumed หมายถึง
ข้อมูลทุกชุดไม่มีเงื่อนไขของการเท่ากันเลือกสถิติทดสอบแล้วเลือก continue จะกลับมาที่หน้าจอรูป
1
![]() 1.3 เลือก Options… จะได้หน้าจอดังรูป
3
1.3 เลือก Options… จะได้หน้าจอดังรูป
3
รูปที่ 3 : Options
![]()
![]() สามารถเลือก -
Descriptive สถิติแบบบรรยาย (X , SD , SE , MAX , MIN )
-
Homogeneity of variance จะหาค่าสถิติทดสอบ Levene ของการ
ทดสอบความเท่ากันของค่าแปรปรวน
แล้วเลือก continue จะกลับมาหน้าจอดังรูปที่
1
สามารถเลือก -
Descriptive สถิติแบบบรรยาย (X , SD , SE , MAX , MIN )
-
Homogeneity of variance จะหาค่าสถิติทดสอบ Levene ของการ
ทดสอบความเท่ากันของค่าแปรปรวน
แล้วเลือก continue จะกลับมาหน้าจอดังรูปที่
1
![]() แล้ว เลือก OK จะได้ผลลัพธ์ในตารางที่ 1 - 3
แล้ว เลือก OK จะได้ผลลัพธ์ในตารางที่ 1 - 3
ตารางที่ 1 Test of Homogeneity of
Variances
|
|
Levene Statistic |
df1 |
df2 |
Sig |
|
income |
18.942 |
3 |
1396 |
.000 |
จากตารางที่ 1
หมายความว่า
ความแปรปรวนของรายได้ครอบครัวนักเรียนของแต่ละโรงเรียนไม่เท่ากัน (Sig = .000)
ตารางที่
2 ANOVA
|
|
Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
Income
of
Between Groups
Within Groups
Total |
168497230601.3 1929890669186 2098387899787 |
3 1396 1399 |
56165743533.772 1382443172.769 |
40.628 |
.000 |
จากตารางที่ 2 หมายความว่า
รายได้เฉลี่ยมีความแตกต่างกันในแต่ละโรงเรียนอย่างน้อย 1 คู่
อย่างมีนัยสำคัญทางสถิติ
จึงต้องทดสอบต่อไปว่าโรงเรียนใดบ้างที่มีรายได้เฉลี่ยต่างกัน โดยใช้วิธี LSD ดังแสดงในผลลัพธ์ ตารางที่ 3
ตารางที่
3 Multiple Comparisons
Dependent Variable : income of respondent
LSD
|
(I )
( J ) School
School |
Mean Difference (
I-J ) |
Std.
Error |
Sig. |
95
% Confidence Interval |
||
|
Lower
Bound |
Upper
Bound |
|
||||
|
1 2
3
4 |
24938.28* 23621.64* 5566.56 |
2674.17 2968.12 3023.31 |
0.000 0.000 0.066 |
19692.45 17799.18 -364.16 |
30184.11 29444.10 11497.27 |
|
|
2 1
3
4 |
-24938.28* -1316.64 -19371.72* |
2674.17 2710.65 2770.97 |
0.000 0.627 0.000 |
-30184.11 .6634.02 .24807.43 |
-19692.45 4000.74 -13936.02 |
|
|
3 1
3
4 |
-23621.64* 1316.64 -18055.08 |
2968.12 2710.65 3055.62 |
0.000 0.627 0.000 |
-29444.10 -4000.74 -24049.18 |
-17799.18 6634.02 -12060.99 |
|
|
4 1 2
3 |
-5566.56 19371.72* 18055.08* |
3023.31 2770.97 3055.62 |
0.066 0.000 0.000 |
-11497.27 13936.02 12060.99 |
364.16 24807.43 24049.18 |
|
·
The mean difference is significant at the
.05 level.
จากตารางที่ 3 หมายความว่า
เมื่อเปรียบเทียบรายได้ของครอบครัวนักเรียนแต่ละโรงเรียน
พบว่าคู่ที่มีรายได้ของครอบครัวนักเรียนที่แตกต่างกัน 4 คู่ ได้แก่
1.
โรงเรียน 1
และ 2
2.
โรงเรียน 1
และ 3
3.
โรงเรียน 2
และ 4
4.
โรงเรียน 3
และ 4
ซึ่งสามารถนำเสนอผลการวิเคราะห์ในตาราง ดังต่อไปนี้
|
โรงเรียน |
รายได้ของครอบครัวนักเรียน |
F -test |
P-value |
|
|
|
ค่าเฉลี่ย |
ส่วนเบี่ยงเบนมาตรฐาน |
|
|
|
1 2 3 4 |
56541.35 31603.07 32919.71 50974.79 |
48285.67 23386.18 23205.95 51427.68 |
40.628 |
0.000 |
|
เปรียบเทียบรายคู่ |
ความแตกต่างของค่าเฉลี่ย ( Mean
Difference ) |
P - value |
|
โรงเรียน 1 2 1
3 1
4 2
3
2 4
3 4
|
24938.28* 23621.64* 5566.56 -1316.64 -19371.72* -18055.08* |
0.000 0.000 0.066 0.627 0.000 0.000 |
2. ประชากรมากกว่าสองกลุ่มที่มีตัวแปรอิสระ 2 ตัวขึ้นไป ( ใช้สถิติ factorial ANOVA )
2.1ใช้คำสั่ง
 Analyze
Analyze
General Linear Model
Univariate…
จะได้หน้าจอแสดงดังรูปที่ 4
รูปที่ 4 : Univariate
จากรูปที่
4 - เลือกตัวแปรตามที่มีระดับการวัด interval ขึ้นไป ใส่ใน dependent เช่น income
![]() -เลือกตัวแปรต้นที่มีระดับการวัดเป็น nominal หรือ ordinal ที่เป็นการจัดประเภทใส่ใน Fixed Factor (s)
-เลือกตัวแปรต้นที่มีระดับการวัดเป็น nominal หรือ ordinal ที่เป็นการจัดประเภทใส่ใน Fixed Factor (s)
2.2 เลือก Models จะได้หน้าจอ
ดังรูปที่ 5
รูปที่
5 : Univariate: Model
จากรูปที่ 5 เลือก Full factorial จะได้อิทธิพลของและปัจจัยและปัจจัยร่วมของปัจจัยต่างๆ
แล้วเลือก continue จะกลับมาหน้าจอดังรูปที่
4
2.3 ![]()
เลือก Contrasts
จะได้หน้าจอ ดังรูปที่ 6
รูปที่
6 : Univariate: Contrasts
การใช้คำสั่ง Contrast เมื่อต้องการทดสอบความแตกต่างของแต่ละระดับของปัจจัย
สามารถเลือกชนิดของ
Contrast ในbox ของContrasts ต่อจากนั้นจึงเลือก continue จะกลับมาหน้าจอดังรูปที่
4
![]() 2.4 เลือก Plots จะได้หน้าจอ
ดังรูปที่ 7
2.4 เลือก Plots จะได้หน้าจอ
ดังรูปที่ 7
รูปที่ 7 Plots
![]() การใช้คำสั่ง Plots จะได้กราฟเส้นตรงที่แต่ละจุดประมาณค่า
เฉลี่ยของตัวแปรตามที่แต่ละระดับของปัจจัย
เมื่อเลือกแล้ว ตามด้วย continue จะกลับมาหน้าจอดังรูปที่
4
การใช้คำสั่ง Plots จะได้กราฟเส้นตรงที่แต่ละจุดประมาณค่า
เฉลี่ยของตัวแปรตามที่แต่ละระดับของปัจจัย
เมื่อเลือกแล้ว ตามด้วย continue จะกลับมาหน้าจอดังรูปที่
4
2.5 เลือก Post
Hoc จะได้หน้าจอ ดังรูปที่ 8
รูปที่8 Post Hoc Multiple Comparison
การใช้คำสั่ง Post Hoc เพื่อเปรียบเทียบเชิงซ้อนของค่าเฉลี่ยแต่ละคู่ เมื่อเลือกแล้ว ตามด้วย continue จะกลับมาหน้าจอดังรูปที่
4

![]() 2.6 เลือก Options… จะได้หน้าจอรูปที่ 9
2.6 เลือก Options… จะได้หน้าจอรูปที่ 9
รูปที่ 9 : Options
![]() จากรูปที่ 9 ผู้วิจัยสามารถเลือก Estimated
Marginal Means , Display , Significance Level แล้วเลือก continue จะกลับมาที่หน้าจอรูปที่ 4 แล้วเลือก OK จะได้ผลลัพธ์แสดงในรูปตารางที่
4
จากรูปที่ 9 ผู้วิจัยสามารถเลือก Estimated
Marginal Means , Display , Significance Level แล้วเลือก continue จะกลับมาที่หน้าจอรูปที่ 4 แล้วเลือก OK จะได้ผลลัพธ์แสดงในรูปตารางที่
4
ตารางที่ 4 ผลลัพธ์ของตัวอย่าง ANOVA
|
|
Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
Income
Model
school
status
2 - Way Interactions sschool*status
Eroor
Total
Corrected Total |
2.6E+12 1.0E+10 2.8E+10 1.0E+10 1.8E+12 4.5E+12 2.0E+12 |
16 3 3 9 1384 1400 1399 |
1.6E+11 3.4E+09 9.5E+09 1.1E+09 1.3E+09 |
120.56 2.51 7.00 0.87 |
.000 0.57 0.00 0.54 |
R Squared =
.582 (Adjusted R Squared = .577)
จากตารางที่ 4 หมายความว่า ตัวแปรต้นหรือ Main Effects มี 2 ตัว ได้แก่ โรงเรียนของนักเรียน( school
) และสถานภาพสมรสของผู้รับผิดชอบครอบครัว
( status ) ตัวแปรตามได้แก่
รายได้ของผู้รับผิดชอบครอบครัว ( income of
respondent ) ก่อนอื่นต้องดูผลของปฏิสัมพันธ์ระหว่างตัวแปรต้น
( 2- way interactions ) ถ้า interaction มีผลต่อรายได้ของผู้รับผิดชอบครอบครัวไม่จำเป็นต้องอ่านผลต่อ แต่ถ้า interaction ไม่มีผลต่อรายได้
ฯ( sig > 0.05) จึงกลับไปดู Main
Effects แต่ละตัว ว่ามีผลต่อรายได้ หรือไม่ ซึ่งจากตารางพบว่าโรงเรียน ไม่มีผลต่อรายได้ของครอบครัว
แต่สถานภาพสมรสมีผลต่อรายได้ของครอบครัว ( sig <0.05 ) ซึ่งสามารถนำเสนอผลการวิเคราะห์ได้ดังนี้
|
ปัจจัยที่มีผลต่อรายได้ ของผู้รับผิดชอบครอบครัว |
F |
P-value |
|
-
โรงเรียน -
สถานภาพสมรส - ปฏิสัมพันธ์ระหว่าง โรงเรียนและสถานภาพสมรส |
2.51 7.00 0.87 |
0.57 .000 0.54 |
แบบฝึกหัด
(ใช้โปรแกรมสำเร็จรูป)
1. อธิการบดีของสถานบันการศึกษาแห่งหนึ่งเชื่อว่ามีนิสิตที่พ้นสภาพการเป็นนักศึกษาโดยเฉลี่ย
ไม่เกิน 13% ของนักศึกษาทั้งหมด จึงสุ่มตัวอย่าง จากคณะ ก. เพียงคณะเดียว
แล้วเก็บข้อมูลร้อยละของนักศึกษาที่พ้นสภาพในปีที่ผ่านมา ย้อนหลัง 12 ปี ได้ข้อมูลดังนี้
13.4 13.3 14.5 11.7 14.0 12.0 15.4 12.3 12.9 12.6 14.9 13.1
จงทดสอบความเชื่อของอธิการบดีของสถานบันการศึกษาแห่งนี้ที่ระดับนัยสำคัญ .05
2. โรงงานแห่งหนึ่งมีคนงาน 2 ชุด ( 2 กะ ) ทางโรงงานเชื่อว่าคนงานกะกลางวันผลิตสินค้าเฉลี่ยต่อวัน
ได้มากกว่าคนงานกะกลางคืน จึงเลือกตัวอย่างคนงานกะกลางวันมา 6 คน กะกลางคืน 9 คน
และตรวจสอบจำนวนชิ้นที่ผลิตได้ต่อวันได้ข้อมูลดังนี้
|
กลางวัน |
41 |
20 |
19 |
36 |
38 |
26 |
|
|
|
|
กลางคืน |
9 |
26 |
16 |
10 |
31 |
28 |
35 |
15 |
10 |
กำหนด a = .01 และถ้าทราบว่าความสามารถในการทำงานของคนงานทั้ง 2 กะมีความแปรปรวนไม่แตกต่างกัน
3. ในการวัดประสิทธิภาพการสอนวิชาสถิติการศึกษา จึงสุ่มนิสิตมา 10
คน ก่อนที่นิสิตจะได้เรียนวิชานี้ แล้วให้ทดสอบความรู้ทางสถิติ
แล้วจึงให้เข้าเรียนวิชาสถิติการศึกษา
เป็นเวลา 4 เดือน
หลังจากเรียนจบแล้วจึงให้สอบใหม่แล้วตรวจสอบคะแนนของนิสิตทั้ง 10 คนข้างต้น ได้ดังนี้
|
นิสิต |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
ก่อนเรียน |
50 |
62 |
51 |
41 |
63 |
56 |
49 |
67 |
42 |
57 |
|
หลังเรียน |
65 |
68 |
52 |
43 |
60 |
70 |
48 |
69 |
53 |
61 |
อยากทราบว่า
การสอนวิชาสถิติการศึกษา
มีประสิทธิภาพหรือไม่ a = .025
4.
โรงเรียนแห่งหนึ่งต้องการทดสอบว่าการเข้าโครงการฝึกปฏิบัติธรรมจะช่วยให้นักเรียนมีผลสัมฤทธิ์ในการทำงานกลุ่มสูงขึ้นหรือไม่
จึงทำการทดสอบกับนักเรียน 10 คน
เก็บคะแนนการทำงานกลุ่มของทุกคน แล้วจึงจัดให้เข้าโครงการฝึกปฏิบัติธรรมนาน 1 เดือน เมื่อสิ้นสุดโครงการแล้ววัดการทำงานกลุ่มของนักเรียนอีกครั้ง ปรากฏว่าได้คะแนน ดังนี้
คะแนนการทำงานกลุ่ม
|
นักเรียน |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
ก่อนเข้าโครงการ |
63 |
93 |
84 |
72 |
65 |
72 |
91 |
84 |
71 |
80 |
|
หลังเข้าโครงการ |
78 |
92 |
91 |
80 |
69 |
85 |
99 |
82 |
81 |
87 |
อยากทราบว่าโครงการฝึกปฏิบัติธรรมทำให้คะแนนการทำงานกลุ่มสูงขึ้นหรือไม่ กำหนดให้ a = .01
5. บริษัทซึ่งผลิตสบู่ออกจำหน่ายต้องการทดสอบตลาดของสบู่ชนิดใหม่
3 ชนิด ( A,B,C ) จึงนำสบู่ออกวางจำหน่ายในปีที่ผ่านมา โดยเก็บยอดขายของสบู่ตามภาคต่าง ๆ
ที่วางขายได้ข้อมูลดังนี้
หน่วย
: 1000 บาท
|
ภาค |
ชนิดของสบู่ A B C |
|
ภาคกลาง ภาคเหนือ ภาคใต้
ภาคอีสาน |
47 57 65
63 63 76
79 67 54
52 50 49 |
อยากทราบว่ายอดขายเฉลี่ยของสบู่ใหม่ทั้ง
3 ชนิดและแต่ละภาคแตกต่างกันหรือไม่ที่ระดับความเชื่อมั่น 95 %
6.
ในห้องปฏิบัติการการทอผ้าแห่งหนึ่งต้องการศึกษาผลของสีพิมพ์ผ้า
4 ชนิด ( A,B,C,D ) เพื่อทำให้สีคงทน ไม่ซีดง่าย
แต่เนื่องจากอาจารย์ผู้สอนคิดว่าชนิดของผ้าที่มีผลต่อคุณภาพของสีด้วย จึงสุ่มตัวอย่างผ้ามา 3 ชนิด ๆ ละผืน แล้วแบ่งผ้าแต่ละผืนเป็น 4 ส่วน เท่า
ๆ กัน กำหนดสีผ้าพิมพ์แต่ละชนิดให้ผ้าแต่ละส่วนอย่างสุ่ม
แล้วทำการทดสอบความคงทนของสีได้ดังนี้
ชนิดของผ้า
1
2
3
|
C 9.9 |
D 13.4 |
B 12.7 |
|
A 10.1 |
B 12.9 |
D 12.9 |
|
B 11.4 |
A 12.2 |
C 11.4 |
|
D 12.1 |
C 12.3 |
A 11.9 |
ก.
จากข้อมูลสรุปได้หรือไม่ว่าคุณภาพของสีพิมพ์ผ้าทั้ง
4 ชนิด แตกต่างกันที่ระดับนัยสำคัญ .10
ข.
อยากทราบว่าชนิดของผ้ามีผลทำให้คุณภาพของสีแตกต่างกันหรือไม่
ที่ระดับนัยสำคัญ .05
7.
ถ้าต้องการเปรียบเทียบประสิทธิภาพของปุ๋ย 3 ชนิด ( ก , ข , ค ) จึงทดลองโดยการสุ่มพื้นที่มา 4 แห่ง แล้วแบ่งพื้นที่แต่ละแห่งเป็น 3 ส่วน
ในแต่ละพื้นที่จะกำหนดชนิดของปุ๋ยแต่ละชนิดให้แต่ละส่วนอย่างสุ่ม ได้ข้อมูลผลผลิต ดังนี้
|
พื้นที่ |
ชนิดของปุ๋ย ก ข ค |
|
1 2 3 4 |
11 15 10 13 17 15 16 20 13 10 12 10 |
จากข้อมูลข้างต้นสรุปได้หรือไม่ว่าปุ๋ยทั้ง
3 ชนิดมีประสิทธิภาพไม่แตกต่างกันที่ระดับนัยสำคัญ 0.05
8. ถ้าต้องการศึกษาความแตกต่างของวัตถุดิบที่ใช้ทำยางรถยนต์
3 ชนิด ขนาดของยางรถยนต์ 3 ขนาด
ว่ามีอิทธิพลต่ออายุการใช้งานของยางรถยนต์หรือไม่ จึงสุ่มรถยนต์มา 36 คัน แล้วสุ่มให้ใช้ยางรถยนต์และขนาดของยางรถยนต์กลุ่มละ 4 คัน ได้ข้อมูล ดังนี้
|
ชนิดของวัตถุดิบ |
ขนาดของยางรถยนต์ |
||
|
เล็ก |
กลาง |
ใหญ่ |
|
|
1 |
78,62,72,68 |
82,78,70,75 |
92,85,87,90 |
|
2 |
65,70,75,69 |
72,68,73,76 |
85,79,84,80 |
|
3 |
81,78,75,85 |
87,83,82,85 |
94,90,89,95 |
ก.
อยากทราบว่ามีอิทธิพลร่วมของขนาดของยางรถยนต์
และชนิดของวัตถุดิบที่มีต่อระยะทางที่วิ่งหรือไม่
ข.
อยากทราบว่าขนาดของยางรถยนต์
มีอิทธิพลต่อระยะทางที่วิ่งหรือไม่
ค.
อยากทราบว่าชนิดของวัตถุดิบมีอิทธิพลต่อระยะทางที่วิ่งหรือไม่
กำหนดระดับนัยสำคัญ = 0.05