บทที่4

ความสัมพันธ์ระหว่างตัวแปรและการทำนายตัวแปร

 

ความสัมพันธ์ระหว่างตัวแปร

          การศึกษาความสัมพันธ์ระหว่างตัวแปร อันเป็นเป้าหมายของข้อสรุปงานวิจัยนั้นก็เพื่อให้เกิดความรู้ ความเข้าใจที่จะสามารถบรรยาย อธิบาย ตลอดจนควบคุมสิ่งต่างๆได้นั้น ค่าสถิติที่นำมาใช้บ่อยมาก คือ ค่าสัมประสิทธิ์สหสัมพันธ์ (rxy ) ซึ่งใช้ได้กับตัวแปร x และ y ที่มีมาตรการวัดแบบอันตรภาคขึ้นไป แต่ยังมีค่าสถิติอีกหลายตัวที่ใช้หาความสัมพันธ์ระหว่างตัวแปรที่อยู่ในเงื่อนไขที่ต่างออกไป ก่อนที่จะอธิบายรายละเอียดของสถิติที่ใช้หาความความสัมพันธ์ระหว่างตัวแปรนั้น เพื่อให้เกิดความเข้าใจในการเลือกใช้สถิติเพื่อศึกษาความสัมพันธ์ระหว่างตัวแปรที่ชัดเจนขึ้น จึงมีความจำเป็นต้องเข้าใจในเรื่องมาตรการวัดของตัวแปร ซึ่งสรุปได้ ดังนี้

การแบ่งประเภทของข้อมูลตามมาตรการวัด    แบ่งเป็น                        

1 มาตรการวัดแบบนามบัญญัติ(Nominal data ) เป็นการจำแนกลักษณะของข้อมูลที่ได้ ออกเป็นประเภทต่างๆหรือเป็นพวกๆ โดยจัดลักษณะที่เหมือนกันไว้ด้วยกัน เช่น ตัวแปร เพศ เชื้อชาติ สถานภาพสมรส  เป็นต้น การจำแนกลักษณะของข้อมูลของตัวแปรเป็น 2 ลักษณะ เรียกว่าตัวแปรทวิวิภาค (Dichotomous Variable) มีรูปแบบในการจำแนกที่แตกต่างกันได้ 2 ลักษณะ คือ ตัวแปรทวิวิภาคแท้ (True dichotomous Variable) และตัวแปรทวิวิภาคจำแนกตามเกณฑ์(Artificially dichotomous Variable) โดยพิจารณาจากเกณฑ์การจำแนกที่มีอยู่แล้ว กับเกณฑ์ที่ต้องสร้างขึ้น ถ้าเกณฑ์ในการแบ่งตัวแปรออกเป็น 2 ลักษณะ เป็นเกณฑ์ที่มีอยู่แล้วเช่น ตัวแปรเพศ แบ่งเป็น หญิงและชาย ก็จัดว่าเป็นทวิวิภาคแท้ แต่ถ้าเป็นเกณฑ์ที่ต้องสร้างขึ้นเช่นการสอบได้ - ตกของนักเรียนก็จัดว่าเป็นทวิวิภาคจำแนกตามเกณฑ์

2 มาตรการวัดแบบอันดับ(Ordinal data ) เป็นการกำหนดลักษณะของข้อมูลที่ได้ ออกเป็นอันดับที่บอกความมากน้อยระหว่างกันได้ เช่นลำดับที่ของนักเรียนมารยาทดี  ค่าลำดับที่ 1 , 2 , 3 สามารถบอกได้ว่าใครมารยาทดีกว่าใคร แต่ไม่สามารถบอกได้ว่าคนที่ได้มารยาทดีลำดับที่ 1 ดีกว่าลำดับที่ 2 อยู่เท่าไร  และไม่สามารถบอกได้ว่าความแตกต่างระหว่างคนที่ได้มารยาทดีลำดับที่ 1และ 2 จะเท่ากับความแตกต่างระหว่างคนที่ได้มารยาทดีลำดับที่ 2 และ 3 หรือช่วงความห่างของค่าตัวแปรแต่ละค่าไม่เท่ากัน

3 มาตรการวัดแบบอันตรภาค(Interval data ) เป็นการกำหนดตัวเลขให้กับลักษณะของข้อมูลตามความมากน้อย โดยตัวเลขที่กำหนดสามารถบอกความมากน้อยระหว่างกันแล้วยังมีช่วงห่างระหว่างค่าที่เท่ากันด้วย แต่ค่าศูนย์ที่กำหนดตามมาตรการวัดนี้ไม่ใช่ศูนย์แท้ ตัวอย่าง เช่น คะแนน อุณหภูมิ  เป็นต้น ค่าของอุณหภูมิ 80°C สูงกว่าอุณหภูมิ 50 °C อยู่ 30°C แต่อุณหภูมิ 0 °C มิได้แปลว่าไม่มีความร้อน ความจริงมีความร้อนระดับหนึ่งแต่ถูกสมมุติให้เป็น 0 °C

4.  มาตราการวัดแบบอัตราส่วน (ratio  data) เป็นการกำหนดตัวเลขให้กับลักษณะของข้อมูลเดียวกับมาตรการวัดแบบอันตรภาค แต่มาตรการวัดระดับนี้จะมีค่า 0 ที่แท้จริงด้วย เช่น อายุ รายได้ น้ำหนัก ส่วนสูง  เป็นต้น    ส่วนสูง 0 เซนติเมตรก็แปลว่าไม่มีความสูงเลย

                เพื่อให้เห็นภาพรวมของสถิติที่ใช้ในการหาความสัมพันธ์ จึงขอเสนอตารางสรุประเบียบวิธีวัดความสัมพันธ์จำแนกตามมาตรวัดตัวแปรก่อนแล้วตามด้วยรายละเอียดของแต่ละวิธีต่อไป

 

สรุประเบียบวิธีวัดความสัมพันธ์จำแนกตามมาตรวัดตัวแปร

 

มาตรวัดตัวแปร

มาตรวัดตัวแปร

 

ทวิวิภาคแท้

ทวิวิภาคจำแนกตามเกณฑ์

อันดับ

 

อันตรภาค/อัตราส่วน

ทวิวิภาคแท้ ( TRUE  DICHOTOMUS)

ทวิวิภาคจำแนกตามเกณฑ์

(ARTIFICIAL  DICHOTOMUS)

อันดับ

อันตรภาค/อัตราส่วน

Ø

Ø

 

rrb

rpb

 

rt e t

 

rrb

rbis

 

 

 

rsr ,τ

 

 

 

 

 

rxy

 

1. สัมประสิทธิ์ ฟี ( Phi correlation)

            เมื่อต้องการหาความสัมพันธ์ระหว่างตัวแปรที่มีมาตรการวัดเป็นทวิวิภาคแท้ทั้งคู่ หรือตัวหนึ่งเป็นทวิวิภาคแท้ อีกตัวหนึ่งเป็นทวิวิภาคจำแนกตามเกณฑ์ จะต้องใช้สัมประสิทธิ์ฟี (Ø)ซึ่งจะได้ขนาดความสัมพันธ์ว่ามีมากน้อยเพียงใด  การหาความสัมพันธ์ของสองตัวแปรเช่นนี้อาจหาได้โดยใช้สถิติ

c2 แต่ c2 จะบอกได้แต่เพียงว่ามีความสัมพันธ์หรือไม่มีความสัมพันธ์เท่านั้น ไม่ได้บอกขนาดความสัมพันธ์

          สูตร                

 ทดสอบความมีนัยสำคัญโดยใช้   c2  หรือ    t-test

 

                              

 

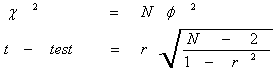
ตัวอย่าง การหาความสัมพันธ์ระหว่างเพศกับการไปโรงเรียน

 

การไปโรงเรียน

เพศ

  รวม

 

ชาย

หญิง

สาย

ไม่สาย

10    (a)

40    (b)

20   (c)

42   (d)

30

82

 

50

62

112

 

 

                                           =         (40r20) - (10r42)

                                                                                                                                                    √  50 r82r30r62

                                           =             380

                                                       2761.52

 =           0.1376

                           

ตัวอย่างอื่น เช่น    หาความสัมพันธ์ระหว่างฐานะเศรษฐกิจกับการไปเลือกตั้ง

 

2. The Tetracholic coefficient

เมื่อต้องการหาความสัมพันธ์ระหว่างตัวแปรที่มีมาตรการวัดเป็นทวิวิภาคโดยจำแนกตามเกณฑ์ ทั้งคู่

              สูตร                          

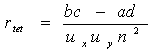
โดยที่ Ux           =    ค่าความสูงของการแจกแจงปกติมาตรฐาน(ordinate)ณ จุดตัด(สัดส่วน)

                           จากตัวแปร x

          Uy            =  ค่าความสูงของการแจกแจงปกติมาตรฐาน(ordinate)ณ จุดตัด(สัดส่วน)

                           จากตัวแปร y

          n          =  ขนาดของกลุ่มตัวอย่าง

 

 

 

 

ตัวอย่าง  การหาความสัมพันธ์ระหว่างความชอบของหวาน กับความชอบผลไม้

 

ความชอบ

ผลไม้(y)

ความชอบของหวาน (x)

ชอบ

ไม่ชอบ

รวม

สัดส่วน

 

ชอบ

ไม่ชอบ

12(a)

32(b)

21(c)

15(d)

33

47

.42

.58

Uy =.3910

รวม

สัดส่วน

44

.55

36

.45

80

 

 

Ux =.3958

                                 

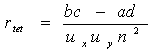
                                                   =      (32r21) - (12r15)

                                                                                                                                                              (.3958)(.3910) r802

                                                                                  =       492

                                                                                                                                                                        990.44

                                             =      0.4967

 

3. The Rank-biserial correlation  coefficient

เมื่อต้องการหาความสัมพันธ์ระหว่างตัวแปรที่มีมาตรการวัดเป็นทวิภาคและอันดับ

                       สูตร         

                โดยที่              y1           =   ค่าเฉลี่ยอันดับของตัวแปรy จากกลุ่มตัวแปร x= 1

                                 y0            =   ค่าเฉลี่ยอันดับของตัวแปรy จากกลุ่มตัวแปร x= 0

ตัวอย่าง  การหาความสัมพันธ์ระหว่างการทำงานบ้านกับอันดับที่ของคะแนน

 

การทำงานบ้าน  (x)

1       0      1      1     1     0     0      1     1     1

อันดับที่ของคะแนน (y)

1       2      3      4     5     6     7      8     9     10

                                      

                                                =       2    ( 5.71 - 5 )

                                                         10

                                                =     0.142

4. The Spearman Rank correlation

เป็นวิธีหาความสัมพันธ์ระหว่างตัวแปร 2 ตัวที่มีมาตรการวัดเป็นอันดับทั้งคู่ มีสูตรในการคำนวณ   คือ

            สูตร              

 

            โดยที่  d  = ความแตกต่างระหว่างอันดับของ 2 ตัวแปร

                       n  = จำนวนกลุ่มตัวอย่าง

            สถิติทดสอบนัยสำคัญ
 
 

 

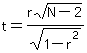
                                      df    =      n-2

ตัวอย่าง   การหาความสัมพันธ์ระหว่าง การให้คะแนนสอบวิชาสถิติ ของอาจารย์ 2 คน

 

นักเรียน

ครู

d

d2

           คนที่1                           คนที่2

คะแนน    อันดับที่        คะแนน    อันดับที่

1

2

3

4

5

     19         1               18             2

     17         3               16             3

     16         4               14             5

     18         2               20             1

     15         5               15             4

1

0

1

-1

-1

1

0

1

1

1

 

                                    สูตร              

                                                                     =   1 -    6 r 4

                                                                                 5(25-1)

                                                                     =   0.8 

            แสดงว่าการให้คะแนนของครู 2 คนมีความสัมพันธ์กันในระดับสูง

      การทดสอบนัยสำคัญ

          H0 :    r  =  0

                       H1   :   r  >  0             

                                                                       

                                                                                                                   

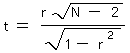
                                                                                                                     =   0.8 √ 5 - 2

                                                                                                                           √1 -  0.82

                                                                                                                      =  0.8 (1.732)

                                                                                                                                   0.6

 

                                                                     =   + 2.30

 

 

 

 


                                                                                                            a  0.10        

                       

                                                                                                               0                  1.63    t (df =5-2 = 3)

 

    t  คำนวณมากกว่าค่าวิกฤต  แสดงว่าปฏิเสธสมมติฐาน H0  นั่นคือ การให้คะแนนของครู 2 คนมีความสัมพันธ์กันอย่างมีนัยสำคัญทางสถิติที่ระดับ 0.10

 

 

5. Kendall’s Tau

เมื่อต้องการหาความสัมพันธ์ระหว่างตัวแปรที่มีมาตรการวัดเป็นอันดับทั้งคู่

สูตร 

โดยที่ จำนวนความสอดคล้อง คือจำนวนอันดับที่ที่เหลือที่สูงกว่าอันดับที่จัดเรียงจากตัวแปรY เทียบตามอันดับที่จากน้อยไปมากของตัวแปรX

           จำนวนความผกผัน คือจำนวนอันดับที่ที่เหลือต่ำกว่าอันดับที่จัดเรียงจากตัวแปรY เทียบตามอันดับที่จากน้อยไปมากของตัวแปรX

          p   =   ผลรวมของจำนวนความสอดคล้อง

          q   =    ผลรวมของจำนวนความผกผัน

          n    =   ขนาดของตัวอย่าง

 ตัวอย่าง  ความสัมพันธ์ระหว่างอันดับที่ของจำนวนสส.และอันดับที่ของบัญชีรายชื่อ

 

ชื่อพรรค

อันดับที่ของจำนวนสส.(x)

อันดับที่ของ

บัญชีรายชื่อ(y)

จำนวนความ

สอดคล้อง

จำนวนความ

ผกผัน

ไทยรักไทย

ประชาธิปปัตย์

ชาติไทย

ชาติพัฒนา

ความหวังใหม่

ประชากรไทย

เสรีธรรม

ถิ่นไทย

1

2

3

4

5

6

7

8

3

1

2

4

7

8

5

6

5

6

5

4

1

0

1

0

2

0

0

0

2

2

0

0

                                                    P=22          Q=6

 

                  

 

                                                 =             22 - 6

                                                                 8(8 -1)/2

                                                   =            16           =         0.57

                                                                 28

6. The Point Biserial Correlation

เมื่อต้องการหาความสัมพันธ์ระหว่างตัวแปรที่มีมาตรการวัดเป็นทวิวิภาคแท้และอันตรภาค/อัตราส่วน

                        สูตร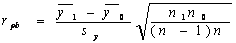         

                        โดยที่ y1           =   ค่าเฉลี่ยของข้อมูลระหว่างตัวแปรy จากกลุ่มตัวแปร x= 1

                            y0            =   ค่าเฉลี่ยของข้อมูลระหว่างตัวแปรy จากกลุ่มตัวแปร x= 2

                                                SY          =   ส่วนเบี่ยงเบนมาตรฐานของข้อมูลจากตัวแปร y ทั้งหมด

 

 

ตัวอย่าง  การหาความสัมพันธ์ระหว่างเพศกับคะแนนสถิติ

เพศ

ช

ช

ช

ช

ช

ญ

ญ

ญ

ญ

ญ

คะแนนสถิติ

15

19

12

9

18

11

16

19

13

7

 

                                     

                                                =   14.6 – 13.2           5 r  5

                                                            4.2          Ö    9r10

                                                =    0.33 r .52                        =    0.17

7. The  Biserial Correlation

เมื่อต้องการหาความสัมพันธ์ระหว่างตัวแปรที่มีมาตรการวัดเป็นทวิภาคตามเกณฑ์และอันตรภาค/อัตราส่วน

                            สูตร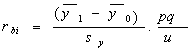       

                โดยที่        y1   =  ค่าเฉลี่ยของข้อมูลระหว่างตัวแปรy จากกลุ่มตัวแปร x= 1

                                               y0   =  ค่าเฉลี่ยของข้อมูลระหว่างตัวแปรy จากกลุ่มตัวแปร x= 0

                           p   =  สัดส่วนของคนที่อยู่ในกลุ่มตัวแปร x= 1

                                              q   =  สัดส่วนของคนที่อยู่ในกลุ่มตัวแปร x= 0

               u   =  ค่าความสูงของการแจกแจงปกติมาตรฐาน(ordinate)ณ จุดตัด(สัดส่วน)

               SY    =   ส่วนเบี่ยงเบนมาตรฐานของข้อมูลจากตัวแปร y ทั้งหมด

ตัวอย่าง  การหาความสัมพันธ์ระหว่างการตอบข้อ 3 กับคะแนนรวม

 

 การตอบข้อ3

คะแนนรวม

การตอบข้อ3

คะแนนรวม

การตอบข้อ3

คะแนนรวม

1

21

1

38

0

26

1

35

1

36

0

35

1

37

0

31

0

36

1

32

0

28

0

21

1

22

0

21

0

23

1

28

0

22

0

25

1

39

0

27

0

27

1

40

0

33

0

26

 

 

 

 

0

25

                                                           

                                                                      =     (32.8  - 27.06) r  ( 0.4 r 0.6)

                                                                                   6.28                  0.3863

                                                                      =   0.91r 0 .621      =   0.565

8.  Correlation coefficient

สหสัมพันธ์อย่างง่าย   (Correlation) เป็นการหาความสัมพันธ์ระหว่างตัวแปรตั้งแต่ 2 ตัวขึ้นไปว่ามีความสัมพันธ์เกี่ยวข้องกันหรือไม่ลักษณะใด และความสัมพันธ์กันมากน้อยเพียงใด   สหสัมพันธ์มีหลายชนิด  ที่รู้จักกันทั่วไปได้แก่ สหสัมพันธ์เชิงเดียว  (Simple   Correlation)  สหสัมพันธ์พหุคูณ

( Multiple  Correlation)   นอกจากนั้นจากสหพันธ์นี้ยังวิเคราะห์ต่อไปได้อีกเช่นการวิเคราะห์ถดถอย

 (Regression  Analysis)

                  สหสัมพันธ์เชิงเดี่ยว  เป็นการหาความสัมพันธ์ระหว่างตัวแปร  2  ตัว  และสมมติว่ามีความสัมพันธ์กันในลักษณะเส้นตรง  ความสัมพันธ์ของตัวแปรของทั้งสองอาจจะสัมพันธ์กันใน  4  ลักษณะ คือ

                  ลักษณะที่ 1  เป็นการสัมพันธ์กันเชิงบวกอย่างสมบูรณ์ มีลักษณะแปรผันตามกัน  เมื่อ X เพิ่ม Y ก็จะเพิ่มขึ้นด้วย  ถ้า X  ลดลง Y    ก็จะลดลงด้วย และเพิ่มขึ้นหรือลดลงในอัตราส่วนที่คงที่  ดังลักษณะ   1

                   ลักษณะที่ 2  เป็นการสัมพันธ์กันเชิงลบอย่างสมบูรณ์ ในลักษณะผกผันกัน เมื่อ X เพิ่ม Y ก็จะลดลงดังลักษณะ  2

                  ลักษณะที่ 3  เป็นการสัมพันธ์กันแบบไม่สมบูรณ์  ซึ่งจะเป็นลักษณะแปรผันตามกันหรือผกผันกันได้  แต่มีลักษณะสัมพันธ์ต่ำ  การสัมพันธ์จะกระจายกัน  แต่ก็ยังเกาะกลุ่มกันทำให้เห็นว่าเป็นเส้นตรง  ดังลักษณะ  3

                  ลักษณะที่ 4  เป็นลักษณะที่ไม่สัมพันธ์กันเป็นเส้นตรง  ค่าของ X  และ  Y  ที่ตัดกันกระจัดกระจายทั่วไป และมีลักษณะคล้ายจะเป็นวงกลม ไม่สามารถบอกความสัมพันธ์ของ X และ  Y ได้ว่าเป็นทิศทางใด ดังลักษณะ  4                                                                                                              

            y                                                                                     y

           

 

 

 

 

 


              ลักษณะ  1                            x                                                           ลักษณะ 2                            x

            y                                                                              y

 

 

 

 

 

 

 


ลักษณะ 3                               x                                   ลักษณะ 4                                                   x

 

ขนาดของความสัมพันธ์

            ขนาดของความสัมพันธ์มีค่าจาก0 ถึง 1.00 สามารถจัดระดับความสัมพันธ์ได้โดยประมาณ ดังนี้

 

ความสัมพันธ์ทางลบอย่างสมบูรณ์                                        ไม่มีความสัมพันธ์                                       ความสัมพันธ์ทางบวกอย่างสมบูรณ์

ลบระดับสูง

ลบระดับกลาง

ลบระดับต่ำ

บวกระดับต่ำ

บวกระดับกลาง

บวกระดับสูง

-1.00               -0.50                               

0                     +0.50                +1.00

 

           

สูตรที่ใช้ในการคำนวณ ค่า r

            r  เรียกว่า  Pearson  correlation coefficiient , Simple correlation , Correlation coefficient

 

 

 

                                               

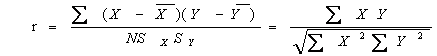
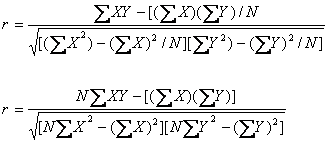
ตัวอย่าง  จากการศึกษาความสัมพันธ์ระหว่างความรู้กับความคิดเห็นของนักศึกษา 5 คน ได้คะแนนความรู้และความคิดเห็น ดังตาราง อยากทราบว่า ความรู้กับความคิดเห็นสัมพันธ์กันหรือไม่ ถ้าสัมพันธ์สัมพันธ์กันในทิศทางใด

            การคำนวณ สมมติให้ X = คะแนนความรู้ และ Y = คะแนนความคิดเห็น จัดระเบียบเตรียมการวิเคราะห์ ดังนี้

          ตาราง   การจัดระเบียบเตรียมการวิเคราะห์สหพันธ์แบบ Pearson

                คนที่               X                              Y                              X2                          Y2                             XY                   1                  5                                   8                            25                          64                               40

                 2                    5                                  9                            25                          81                               45

                 3                  4                                   8                            16                          64                               32

                 4                   3                                   6                              9                           36                               18

                 5                 3                                    7                              9                           49                               21

                รวม              20                              38                            84         294                           156

การคำนวณค่า r

                            

 

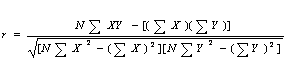
                                 =           5 (156)-(20)(38)

                                       √(5(84)-400) (5(294)-(1444)    

                                 =                       20

                                                        √   (20)(26)

                                 =                     0.877

สัมประสิทธิ์สหสัมพันธ์ เท่ากับ 0.877 แสดงว่าความสัมพันธ์ระหว่างความรู้กับความคิดเห็นของนักศึกษา มีความสัมพันธ์ในทางบวกระดับสูง

การทดสอบนัยสำคัญของค่า r

                  ในการวิจัยนั้น หลังจากที่คำนวณค่าสัมประสิทธิ์สหสัมพันธ์ได้แล้ว และต้องการที่จะสรุปว่าตัวแปรคู่นั้นมีความสัมพันธ์กันจริงหรือไม่ จะไม่พิจารณาเฉพาะค่าสัมประสิทธิ์สหสัมพันธ์ที่คำนวณได้ กล่าวคือถึงแม้ว่าจะคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ได้ค่าหนึ่งซึ่งค่อนข้างสูง เช่น .70 ขึ้นไป ก็จะยังไม่สรุปว่าตัวแปร 2 ตัวนั้นมีความสัมพันธ์กันจนกว่าจะมีการทดสอบนัยสำคัญก่อน (Test of significance) ซึ่งตั้ง H0 และ H1 ดังนี้ H0 : r = 0, H1 : r ¹ 0 (Welkowitz.  1971 : 158)

                  วิธีทำสอบมี 2 วิธี คือใช้ตารางสำเร็จที่มีชื่อว่าค่าวิกฤตของสหสัมพันธ์แบบเพียร์สัน หรือใช้การทดสอบค่าที (t-test) จากสูตร
 
 

 

 


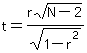
                  r     แทน  ค่าสัมประสิทธิ์สหสัมพันธ์ที่คำนวณได้

                  N    แทน  จำนวนข้อมูลหรือจำนวนคน

                  วิธีการทดสอบมีขั้นตอนดังนี้

                  (1)  คำนวณค่า t จากสูตร

                  (2)  เปิด Table  หาค่า t ที่ df = N-2  ณ ระดับนัยสำคัญทางสถิติที่ตั้งไว้

                  (3)  เปรียบเทียบค่า t ที่คำนวณได้กับค่า t ที่เปิดจากตาราง

                  ถ้า t คำนวณ > t ตาราง แสดว่าค่า r ที่คำนวณได้มีนัยสำคัญทางสถิติ แปลความหมายได้ว่า ตัวแปร 2 ตัวนั้นมีความสัมพันธ์กันอย่างมีนัยสำคัญทางสถิติที่ระดับ…

                  ถ้า t คำนวณ < t ตาราง แสดงว่าค่า r ที่คำนวณได้ไม่มีนัยสำคัญทางสถิติ แปลความได้ว่า ตัวแปร 2 ตัวนั้นมีความสัมพันธ์กันอย่างไม่มีนัยสำคัญทางสถิติ

ตัวอย่างการทดสอบนัยสำคัญ

                  ตัวอย่างที่….จงทดสอบนัยสำคัญของค่า r เมื่อ r = .877
 
 


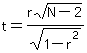
                  สูตร

 

                        r = .877 , N = 5
 
 

 

 


           

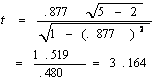
จากตาราง t ที่ a .10, df = 5-2 = 3, ได้ t = 2.353

            t คำนวณ > t ตาราง แสดงว่า r = .877 ที่คำนวณได้มีนัยสำคัญทางสถิติ นั่นคือ มีความสัมพันธ์ระหว่างความรู้กับความคิดเห็นของนักศึกษา อย่างมีนัยสำคัญทางสถิติที่ระดับ 0.10

 

 

 

 

 

 

การทดสอบความสัมพันธ์ระหว่างตัวแปร  2  ตัว โดยใช้โปรแกรม  SPSS for Windows

            การทดสอบความสัมพันธ์ระหว่างตัวแปร  2  ตัว สามารถการวิเคราะห์ โดยใช้โปรแกรม  SPSS for Windows  ได้ดังนี้

            1. ความสัมพันธ์ระหว่างตัวแปร  2  ตัว ที่มีระดับการวัดเป็น ordinal (ใช้สถิติ Spearman Rank correlation )        

            2. ความสัมพันธ์ระหว่างตัวแปร  2  ตัว ที่มีระดับการวัดเป็น interval หรือ  ratio  ( ใช้สถิติ pearson  product   moment  correlation )

                        1.1 ใช้คำสั่ง

                                                Statistics

                                                       Correlate

                                                            Bivarriate

 

จะได้หน้าจอ ดังรูปที่1

รูปที่ 1


 

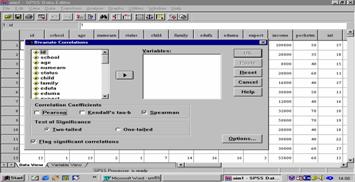
            เลือก ตัวแปรที่ต้องการหาความสัมพันธ์ใส่ใน   box ของ  variables แล้วเลือก Spearman ในกรณีที่ต้องการหาความสัมพันธ์ของ 2 ตัวแปรที่มีระดับการวัดแบบ ordinal  หรือเลือก Pearson  ในกรณีที่ต้องการหาความสัมพันธ์ของ 2 ตัวแปรที่มีระดับการวัดแบบ interval หรือ ratio    แล้วเลือก   OK    จะได้ผลลัพธ์แสดงในตารางที่ 1-2

 

 

 

 

 

 

ตารางที่ 1          Spearman's rho

 

 

 

 

 

 

 

 

 

 

EDUFA

EDUMA
  Spearman's                               rho

   EDUFA

Correlation Coefficient

1.000

.729
 

 

Sig. (2-tailed)

.

.000
 

 

N

1408

1406
 

   EDUMA

Correlation Coefficient

.729

1.000
 

 

Sig. (2-tailed)

.000

.
 

 

N

1406

1421
**  Correlation is significant at the .01 level (2-tailed).

            จากตารางที่ 1 หมายความว่า  การศึกษาของบิดา  ( Edufa )  มีความสัมพันธ์การศึกษาของมารดา (Eduma) อย่างมีนัยสำคัญทางสถิติที่ระดับ .01

            ซึ่งสามารถนำเสนอผลการวิเคราะห์ข้อมูล  ได้ตามตารางต่อไปนี้

 

ตัวแปร

Spearman's rho

p - value

การศึกษาของบิดา

การศึกษาของมารดา

.956

0.000

 

ตารางที่  2 Pearson  correlation

 

Total   Expense

income  of    respondent

Pearson               Total  Expense

Correlation         income  of  respondent

1.000

.956

.956

1.000

Sig.                    Total  Expense

( 1- tailed )          income  of  respondent

.

.000

.000

.

 N                       Total  Expense

                           income  of  respondent

90

90

90

90

           

            จากตารางที่ 2 หมายความว่า  ค่าใช้จ่าย  ( Expense )  มีความสัมพันธ์กับ รายได้ของผู้รับผิดชอบครอบครัว  ( income  of  respondent ) อย่างมีนัยสำคัญทางสถิติที่ระดับ .01

            ซึ่งสามารถนำเสนอผลการวิเคราะห์ข้อมูล  ได้ตามตารางต่อไปนี้

ตัวแปร

r

p - value

ค่าใช้จ่าย -รายได้

.956

0.000

 

การทำนายตัวแปร : การวิเคราะห์ถดถอย (Regression  Analysis )

การวิเคราะห์การถดถอย เป็นสถิติที่ใช้ในการทำนายตัวแปรวิธีหนึ่ง เมื่อมีตัวแปรต้นหรือตัวแปรอิสระเพียงตัวเดียว  และต้องการทดสอบว่าตัวแปรต้นนั้นมีความสัมพันธ์กับตัวแปรตามอย่างไร ในกรณีที่มีตัวแปรเพียง 2 ตัวเช่นนี้การวิเคราะห์การถดถอยนี้เรียกว่า Bivariate  regression หรือ Simple regression  ถ้า plot จุด โดยให้แกน X เป็นจำนวนครั้งของการไปซื้อสินค้า และแกน Y เป็นทัศนคติของผู้บริโภคที่มีต่อห้างสรรพสินค้า จะได้รูป Scatter  diagram ดังนี้

 

การ Plot ข้อมูลทัศนคติที่มีต่อห้างสรรพสินค้าและจำนวนครั้งที่ผู้บริโภคไปซื้อสินค้า

       Y ( ทัศนคติ )                                                                                             

 

                                                                                                              X

                                                                                    X

                                                                                X                              X

                                                                                                                X

                                                                                                X

                                                                X

                                                X

                                X

                                                                                                                                                                                                                                             X    จำนวนครั้งที่ไปซื้อสินค้า

            การพิจารณา Scatter  diagram  จะทำให้สามารถมองเห็น “ รูปร่าง ” ของความสัมพันธ์ระหว่างตัวแปรทั้ง 2 ตัวได้ จะสังเกตได้ว่าเมื่อตัวแปร X เพิ่มขึ้น ตัวแปร Y ก็มีแนวโน้มเป็นความสัมพันธ์เชิงเส้นตรง(Linear relationship )เทคนิคในการ Fit ตัวแบบจำลอง ( Model ) ให้สามารถอธิบายข้อมูล (Data) ได้นั้นเรียกว่าเทคนิค Least - square เทคนิคนี้จะกำหนดเส้นตรงที่ดีที่สุด  โดยที่เมื่อลากเส้นตรงเส้นนี้ระหว่าง Plot บน Scatter diagram แล้ว ผลรวมของความแตกต่างระหว่างจุดทุกจุดที่ห่างจากเส้นตรงรวมกันจะต้องมีค่าน้อยที่สุด เส้นตรงเส้นที่ดีที่สุดนี้เรียกว่า เส้น Regression line หรือ เส้นสมการถดถอย ระยะตั้งฉากระหว่างจุดที่ plot กับเส้นตรง เรียกว่า Error ระยะห่างจากจุดทุกจุดที่ Plot กับเส้นตรงเมื่อยกกำลัง 2 และนำมาบวกรวมกันเรียกว่าผลรวมของความคลาดเคลื่อนยกกำลังสอง ( Sum of squared errors )  å ei2  จะต้องมีค่าน้อยที่สุด เส้น Regression line ที่ดีที่สุดจึงถูกเรียกว่า  The  regression line of Y on X                   สมการ Bivariate  regression ของเส้นตรง regression line สามารถเขียนได้ดังนี้

 


                                                U  =  a + bC + ei

 

                        โดยที่    U  =     ตัวแปรตาม ( Dependent or criterion variable ) หรือยอดขาย

                                    C  =     ตัวแปรอิสระ ( Independent or predictor variable ) ตัวที่ 1

                                    a  =     ค่าคงที่ ( Intercept of the line )

                                    b  =     ค่าความชันของเส้น ( Slope of the line )

                                    eI    =     ความคลาดเคลื่อนที่เกิดขึ้นเนื่องจาก Y แตกต่างจาก Y        

การประมาณค่า  a และ b ด้วย a และ b โดยใช้วิธีกำลังสองน้อยที่สุด          ซึ่งเป็นวีธีหาค่า a และb ที่ทำให้ผลบวกของค่าความคลาดเคลื่อนยกกำลังสองมีค่าน้อยที่สุด

          จากสมการ                    U  =  a + bC + eI

          และ                         U  =  a + bC

ทำให้สามารถคำนวณหาค่า ของ   a  และ  b  คือ   

                                                                        b   =    n å  xi   yi     -  ( å xi ) (å yi  )

                                                                                        n å xi2    -   ( å xi ) 2

                                                                             =             SSxy

                                                                                                                                                                SSxx

 

                                                                                  a =  U  -  b C

                                    โดยที่    C  =      å xI              และ U    =   å yI

                                                              n                                                  n

 

 

ตัวอย่างที่1 การวิเคราะห์สมการถดถอยอย่างง่าย : สมมติให้ผู้ประกอบการแห่งหนึ่งต้องการตรวจสอบดูว่าการใช้ความถี่ของโฆษณาในทางโทรทัศน์ต่อเดือน  มีความสัมพันธ์อย่างไรกับยอดขายของกิจการจึงเก็บตัวอย่างยอดขายและจำนวนความถี่ของโฆษณาในทางโทรทัศน์ต่อเดือนได้ข้อมูลดังนี้

 

ยอดขาย  (U )    ( หน่วย : พันบาท )          จำนวนครั้ง / เดือนของการโฆษณาทางโทรทัศน์ (C )

                            260.3                                                                                                                5

                                     286.1                                                                                                   7

                                     279.4                                                                                                   6

                                     410.8                                                                                                   9

                                     438.2                                                                                                 12

315.3                                                                                                                                                    8                                                                                                       

                                 656.1                                                                                                     11       

570.0                                                                                                                                                 16                                                                                                                                                                

                                 426.1                                                                                                     13

315.0                                                                                                                                                    7

                                          10

                                    å  Ui  =  ( 260.3 + 286.1 + .... + 315.0 )          =          3,866.3

                                                                          i=1

                                                                        10

                                    å  Ci   =  ( 5+7+ ... +7 )                                    =          94

                                    i=1

                                    10

                                    å  CIUi =  5(260.3)+7(286.1)+...+7(315.0)       =           39,539          

                                    i=1

                                    10

                                    å  C2                =  52+72+...+72                                                                           =           994

                                    i=1

                                                                          U        =  260.3+286.1+...+315.0       = 3,866.3       =  386.63

                                                                   10                                 10

                                     C         =  5+7+...+7                  =  94             = 9.4

                                                             10                            10

                                       \     b                             =     n å  CiUi - (å  Ci     ) ( åUi   )

                                                                                i=1         i=1        i=1

                                                                                       n               n

                                                                                     n å  Ci 2    -  (å  Ci    )2   

                                                                                                        i=1            i=1  

                                                                    

                                                            =     10(39,539)-(94)(3866.3)

                                                                          10(994)-(94)2

                                                            =    395,390-363,432.2

                                                                        9940 - 8836

                                                            =    31,957.8                =  28.947

                                                                                                                                   1104         

                                                                        \a                  =          U   -     b C 

                                                            =          386.63 - 28.95(9.4)

                                                            =          386.63-272.13             =  114.5

ดังนั้นสมการถดถอยจะเขียนได้ดังนี้

                                                U         =          114.5 + 28.95 (Ci  )

            ถ้าแทนค่า Ci    ใดๆ ลงในสมการก็จะคำนวณหาค่า U ( ยอดขายโดยเฉลี่ย ) ได้จากสมการ

ถดถอยข้างต้นสามารถอธิบายได้ว่ายอดขายจะเพิ่มขึ้น 28,950 บาท สำหรับการเพิ่มความถี่ของโฆษณาทางโทรทัศน์ขึ้นจากเดิม 1 ครั้ง (b = 28.95) ถ้าไม่มีการโฆษณาทางโทรทัศน์เลยยอดขายจะเท่ากับ 114,500 บาท (a = 114.5 )

 

ตัวอย่างที่ 2  คอลัมน์ที่ 2 และ 3 ในตารางแสดงค่าคะแนน I.Q. (X) และคะแนนการอ่านที่ได้จากการสอบ (Y) ของนักเรียน 18 คน คอลัมน์ 4 แสดงค่า X2 และคอลัมน์ 5 แสดงค่าของผลคูณ XY

 

(1)

นักเรียนคนที่

(2)

คะแนน IQ

X

(3)

คะแนนการอ่าน

Y

(4)

 

X2

(5)

 

XY

(6)

ค่าที่พยากรณ์ได้

Y

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

118

99

118

121

123

98

131

121

108

111

118

112

113

111

106

102

113

101

66

50

73

69

72

54

74

70

65

62

65

63

67

59

60

59

70

57

13,924

9,801

13,924

14,641

15,129

9,604

17,161

14,641

11,664

12,321

13,924

12,544

12,769

12,321

11,236

10,404

12,769

10,201

7,788

4,950

8,614

8,349

8,856

5,292

9,694

8,470

7,020

6,882

7,670

7,056

7,571

6,549

6,360

6,018

7,910

5,757

68

55

68

70

71

54

77

70

61

63

68

64

65

63

60

57

65

57

ผลรวม

2,024

1,155

228,978

130,806

 

Y = (คะแนนการอ่าน)

                        80

                        75

                        70

                        65

                        60

                        55

                        50

                                                                                                                                         X = (I.Q)

                                          100    105  110  115   120   125  130   135  140  145

                                                  รูปที่ 3  แผนภาพกระจัดกระจาย

            เมื่อรวมค่าต่าง ๆ ในคอลัมน์ 2, 3, 4, 5 จะได้ผลดังนี้          

 
 

 

 

 

 

 

 

 

 


                   

 

ดังนั้น เส้นถดถอยสำหรับพยากรณ์ค่า Y เมื่อทราบค่า X เขียนอยู่ในรูปของสมการได้เป็น

                                    Y = 0.6708 X – 11.25

                  เมื่อแทนค่า X ใด ๆ ในสูตรนี้ จะได้ Y ซึ่งเป็นค่าประมาณของ Y

                  เช่น แทนค่า X = 118 จะได้ Y = 0.6708 (118) – 11.25 = 68

                  คอลัมน์  6  ในตาราง แสดงค่าคะแนนการอ่านที่ประมาณได้  (Y)  จากการใช้สมการ

                                    Y = 0.6708 X – 11.25

 

การทดสอบสมมติฐานเกี่ยวกับ b

                เป็นการทดสอบว่าตัวแปร XและY มีความสัมพันธ์ในลักษณะเชิงเส้นหรือไม่ โดยเป็นการทดสอบสมมติฐานแบบ 2 ข้าง

จากสมการถดถอย                          U  =  a + bC + eI

ถ้า b  =  0   แสดงว่า XและY ไม่มีความสัมพันธ์ในลักษณะเชิงเส้น โดยมีสมมติฐาน คือ

H0         :       b    =  0   หรือ XและY ไม่มีความสัมพันธ์ในลักษณะเชิงเส้น

H1         :       b   ¹  0   หรือ XและY มีความสัมพันธ์ในลักษณะเชิงเส้น

สถิติทดสอบ   t      =        b  -   0           =            b

                                                          sb                             s yx  /  Ö ssxx

 

โดยที่     Syx =  ÖS (Y-Ý )2 / n – 2                                     SSxx   = SX2  - (SX)2/ n                                                                  

 

 การทดสอบสมมติฐานเกี่ยวกับ a

                เป็นการทดสอบว่าตัวแปร Y=0แล้ว Xจะเท่ากับ 0 หรือไม่ โดยเป็นการทดสอบสมมติฐาน

H0         :      a  =  0  

H1         :      a ¹  0  

สถิติทดสอบ   t      =        a  -   0                                                           

                                                         sa                                              

                       sa         =    s2 yx (1/n + x 2 / ssxx  ) 

 

ความคลาดเคลื่อนมาตรฐานในการพยากรณ์ (Standard error of estimate)

ถ้าข้อมูล 2 ชุดที่มาหาความสัมพันธ์กันนั้นคล้อยตามกันไม่เป็นเส้นตรง (rxy ¹ 1) ในการพยากรณ์ค่าตัวแปรตัวหนึ่งจากตัวแปรอีกตัวหนึ่งจะมีความคลาดเคลื่อนเกิดขึ้น ถ้าสัมประสิทธิ์สหสัมพันธ์(rxy) ที่คำนวณได้มีค่าสูง ความคลาดเคลื่อนก็จะน้อย ถ้าสัมประสิทธิ์สหสัมพันธ์ (rxy) ที่คำนวณได้มีค่าต่ำ ความคลาดเคลื่อนก็จะมาก ความคลาดเคลื่อนมาตรฐานในการพยากรณ์จะมีค่ามากน้อยเท่าใด คำนวณได้จากสูตรนี้

            (1)  กรณีพยากรณ์ค่า Y เมื่อทราบค่า X
 
                       

                        สูตร

 

            (2)  กรณีพยากรณ์ค่า X เมื่อทราบค่า Y
 
 


                        สูตร

 

            เมื่อ       Syx        แทนความคลาดเคลื่อนมาตรฐานในการพยากรณ์ค่า Y เมื่อทราบค่า X

                        Sy         แทนความเบี่ยงเบนมาตรฐานของคะแนนชุด Y

                        Sxy        แทนความคลาดเคลื่อนมาตรฐานในการพยากรณ์ค่า X เมื่อทราบค่า Y

                        Sx         แทนความเบี่ยงเบนมาตรฐานของคะแนนชุด X

                        R          แทนสัมประสิทธิ์สหสัมพันธ์ที่คำนวณได้

            ข้อสังเกต ถ้า rxy มีค่าเป็น 1 ความคลาดเคลื่อนมาตรฐานในการพยากรณ์จะมีค่าเป็น0

 

การวิเคราะห์ถดถอยเชิงซ้อน ( Multiple regression )

            สมการการถดถอยเชิงซ้อน ( Multiple regression equation ) มีรูปแบบคล้ายคลึงกับสมการการถดถอยอย่างง่าย ( Simple regression equation ) เพียงแต่ว่าสมการถดถอยเชิงซ้อนจะมีตัวแปรอิสระ C มากกว่า1 ตัวขึ้นไป  สมมติให้นักวิจัยสนใจตัวแปรอิสระ  C  3 ตัว  ( C1 , C2  และ  C3 ) ว่าจะมีผลกระทบโดยตรงต่อยอดขาย (U)   สมการถดถอยเชิงซ้อนในรูปแบบความสัมพันธ์เชิงเส้นตรงสามารถเขียนได้แบบง่ายๆ ดังนี้

                                    U         =          a + b1C1 + b2C2 + b3C3  +  e

                        ถ้าหากต้องการเขียนสมการข้างต้นดังกล่าวอย่างถูกต้องอาจจะเขียนใหม่ได้ดังนี้

                                    U123      =          a123 + bU1.23  C1 + bU2.13  C2 + bU3.12  C3  +  e(123)    

                        โดยที่    U123     คือ  ค่าของ U  ที่คาดคะเนได้จากสมการถดถอยเชิงซ้อน

                                     U        คือ ตัวแปรตาม และ C1 , C2  และ  C3  คือตัวแปรอิสระ

                                    a123      คือ  ค่า Intercept  ของสมการถดถอยเชิงซ้อน

                                     bU1.23  คือ  ค่า Coefficient ค่า C1 ในสมการถดถอยเชิงซ้อน ค่า bU1.23  นี้มีชื่อเรียกอีก ชื่อหนึ่งอย่างเป็นทางการว่า Coefficient of partial regression

bU1.23  เป็นค่าที่แสดงถึงการเปลี่ยนแปลงของตัวแปรตาม U เมื่อตัวแปรอิสระ C1 เปลี่ยนแปลงไป 1 หน่วย เลข 1 หลัง U หมายถึงตัวแปรอิสระ C1 ( Predictor variable  ตัวที่ 1 ) ส่วนเลข 2 และ3 หลัง จุดทศนิยมนั้น    บอกให้ทราบว่ายังมีตัวแปรต้น หรือ Predictor  variable อีก 2 ตัว      คือ  C2  และ  C3  ที่มีค่าคงที่  ดังนั้น  bU2.13  และ  bU3.12     จะมีความหมายในทำนองเดียวกัน

            e(123)      คือ  ค่าความผิดพลาดที่เกี่ยวข้องกับการพยากรณ์ค่า U  โดยที่มี C1 , C2  และ  C3   เป็นตัวแปรอิสระ

           

ค่าประมาณของY คือ         y  =    a+ b1 x1+b2x2 +b3x3+….+e

            โดยที่ a คือ ระยะตัดแกน Y กับX เมื่อกำหนดให้ x1 = x2 = x3 = 0

               b1,   b2,     b3 เป็นค่าซึ่งแสดงความสัมพันธ์ระหว่าง Y กับX   และมีความหมาย ดังนี้

   b1 หมายถึง ถ้า x1 เพิ่มขึ้น 1 หน่วยจะทำให้ Y เปลี่ยนแปลงไป b1 หน่วย โดยที่ตัวแปรอิสระอื่นๆ (x2 , x3) มีค่าคงที่  ส่วน b2 และ   b3 จะมีความหมายในทำนองเดียวกัน

            ในกรณีที่แปลงสัมประสิทธิ์การถดถอย (b) ให้เป็นสัมประสิทธิ์การถดถอยมาตรฐาน (b)จะเขียนสมการได้เป็น

                                Zy     =      b1zx1 +b2zx2 +b3zx3 +…+ e

ข้อตกลงเบื้องต้นของ Multiple regression

1.      ตัวทำนายแต่ละตัวและตัวแปรเกณฑ์มีความสัมพันธ์เชิงเส้นตรง

2.      ตัวแปรเกณฑ์ต้องมีลักษณะต่อเนื่อง และอย่างน้อยควรอยู่ในมาตราอันตรภาค

3.      ความแปรปรวนของความคลาดเคลื่อน ในทุก ๆ ค่าของตัวแปร x จะมีค่าเท่ากัน

4.      ตัวทำนายจะต้องไม่สัมพันธ์กันเองสูง ( ไม่เกิด multicollinearity )

5.      การแปรค่าของตัวแปรตามแต่ละค่าต้องเป็นอิสระจากกัน

6.    การแจกแจงของความคลาดเคลื่อนจะต้องเป็นNormality

การทดสอบสมมติฐานเกี่ยวกับสัมประสิทธิ์ความถดถอย( b)

                เป็นการทดสอบว่าตัวแปร X อย่างน้อย 1 ตัว Y มีความสัมพันธ์กับY โดยมีสมมติฐาน คือ

H0         :       bi    =  0  

H1         :       b i ¹  0  ; i = 1,2 ,…,k

สถิติทดสอบ   t      =        bi  -   0          

                                                         sbi                                             

สัมประสิทธิ์การทำนาย ( Coefficient of determination ,R2)

            สัมประสิทธิ์การทำนาย เป็นสัดส่วนที่ตัวแปรอิสระสามารถอธิบายความผันแปรของตัวแปร Y ได้  ใช้สัญลักษณ์ R2 y.123…k

      โดยที่     R2     =   ความผันแปรเนื่องจากอิทธิพลของX1, X2, … Xk

                                                                                       ความผันแปรทั้งหมด

                             =   SSR/SST     =    (SST –SSE) / SST

R2 เข้าใกล้ 1 มากเท่าไรแสดงว่าความผันแปรของตัวแปร y ถูกอธิบายได้ด้วยตัวแปรอิสระมากเท่านั้น

 

สัมประสิทธ์พหุคูณ (Multiple correlation , R )

      สัมประสิทธ์พหุคูณ ได้จากการถอดรากที่สองของสัมประสิทธิ์การทำนาย โดยที่สัมประ

สิทธ์พหุคูณแสดงถึงความสัมพันธ์ระหว่าง Y กับ X1, X2, … Xk   ถ้ามีค่าเข้าใกล้ศูนย์แสดงว่า Y กับ X1, X2, … Xk มีความสัมพันธ์น้อยมาก ถ้ามีค่าเท่ากับ 0 แสดงว่า Y กับ X1, X2, … Xk ไม่มีความสัมพันธ์กัน  ถ้า มีค่าเข้าใกล้ 1 แสดงว่า Y กับ X1, X2, … Xk มีความสัมพันธ์กันมาก

การทดสอบการทำนายตัวแปรโดยใช้โปรแกรม  SPSS for Windows

1.      การทำนายตัวแปรเกณฑ์  1  ตัว จากตัวแปรทำนาย  1 ตัว ใช้สถิติ Simple  regression 

analysis 

ตัวอย่าง  ถ้าต้องการศึกษาว่ารายได้ของครอบครัวเป็นตัวทำนายรายจ่ายของครอบครัวได้หรือไม่ แสดงว่ามีแปรเกณฑ์  1  ตัวได้แก่ รายจ่ายของครอบครัว  ตัวแปรทำนาย 1 ตัว ได้แก่ รายได้ของครอบครัว

สามารถใช้โปรแกรม  SPSS for Windows  ได้ดังนี้

                       1ใช้คำสั่ง

            Analyze

                 Regression

                           Linear                     จะได้หน้าจอดังแสดงในรูปที่ 1

 


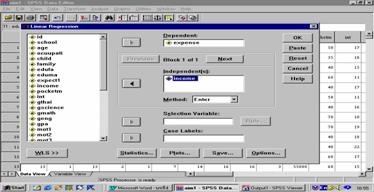
                                   รูปที่ 1 Linear Regression

            จากรูปที่ 4  เลือกตัวแปรเกณฑ์  1  ตัว คือ รายจ่ายของครอบครัว  ใส่ใน box  ของ dependent  และเลือกตัวแปรทำนาย คือ รายได้ของครอบครัว ใส่ใน box ของ independent   เลือก  method

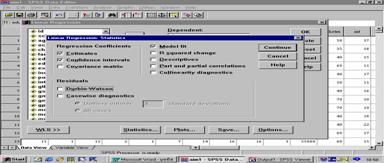
              2  เลือก        statistics       จะได้หน้าจอดังรูปที่ 2

 


รูปที่  2  Linear Regression : Statistics

 

            3.  เลือกสถิติที่ต้องการแล้วเลือก     continue     จะกลับมาหน้าจอเดิมรูปที่  1   เลือก      OK      จะได้ผลลัพธ์ในตารางที่ 2-4

ตารางที่  2 Model  Summaryb

Model

R

R Square

Adjusted  R

Square

Std.Error of the Estimate

 

Durbin-Wastson

1

.956b

.914

.913

2105.6496

2.000

Predictors(Constant),income of respondent   

จากตารางที่ 3 หมายความว่า  รายได้ของครอบครัวสามารถอธิบายความผันแปรของรายจ่ายได้  91.4%(R a =.914)

ตารางที่ 3  ANOVAb

Model

Sum  of  Squares

df

Mean  Square

F

Sig.

1           Regression

             Residual

             Total

4166635796.39

390170915.834

4556806712.22

1

88

89

416635796

4433760.407

939.752

.000

a  . Predictors :   ( Constant ) , income of  respondent

ตารางที่ 4  ANOVA  แสดงถึงตารางวิเคราะห์ความแปรปรวนของสมการ

Expense =  a + b Income + e  สำหรับการทดสอบสมมติฐาน

H0 : Expense  ¹  a + b Income + e   หรือ H0 : b  = 0

H1 : Expense  =    a + b Income + e    หรือ H1 : b  ¹0

สถิติทดสอบ    F =  MSRegression   =  4166635796 = 939.572

                        MS Residual           4433760.407

จะปฏิเสธสมมติฐาน  H0  ถ้า  F > F 1., 88,:.95  = 3.84   เนื่องจาก F =  939.572  จึงปฏิเสธ  H0 หรือตัวแปร  expense  สัมพันธ์กับตัวแปร  income  ในรูปเชิงเส้น

ตารางที่ 4  Coefficients

 

Unstandardizes

Coefficients

Standardized

Coefficients

 

 

95 % Confidence

Interval  for B

 

Model

B

Std. Error

Beta

t

Sig

Lower

Bound

Upper

Bound

1    ( Constant)

      income  of

      respondent

438.720

 

.729

520.416

 

.024

 

 

.956

.843

 

30.7

.402

 

.000

-595.498

 

.682

1472.938

 

.776

 

ตารางที่  5    Coefficients จะแสดงสัมประสิทธิ์ความถดถอย

a   =  438.72  บาท   SE. (a )  = 520.416  บาท

b  =  .729  บาท       SE (b)    = .024  บาท

            ฺBeta  =   b  S x    = .956

                                S y

ก. สมมติฐาน    H0 : b  = 0  เป็นการทดสอบว่ารายได้และรายจ่ายสัมพันธ์กันในรูปเชิงเส้นหรือไม่

                       H1 : b  ¹0 

    สถิติทดสอบ  :  t = 30.7   Sig. ของสถิติทดสอบ t = .000   จึงปฏิเสธ H0 หรือ b¹0  นั่นเอง  เมื่อมีตัวแปรอิสระเพียงตัวเดียว  สถิติทดสอบ   t2 = F และผลสรุปจะเหมือนกัน

ข. สมมติฐาน    H0 : a = 0  เป็นการทดสอบเกี่ยวกับส่วนการตัดแกน Y

                       H1 : a ¹0 

     สถิติทดสอบ    t = .843  Sig ของ  t = .402  > .05  จึงยอมรับ H0 หรือ b = 0

            ดังนั้นผลการทดสอบโดยสถิตทดสอบ F และ t  สรุปได้ว่าสมการความถดถอยซึ่งแสดงความสัมพันธ์ระหว่าง รายได้และรายจ่ายเป็น

                     Exp^ense     =    0.729  Income

            2.  การทำนายตัวแปรเกณฑ์  1  ตัว จากตัวแปรทำนายมากกว่า 1 ตัว ใช้สถิติ Multiple  regression  analysis

          ตัวอย่าง  ถ้าต้องการศึกษาว่ารายได้ของครอบครัว และเกียรติภูมิในอาชีพของบิดาเป็นตัวทำนายเงินที่บุตรได้ไปโรงเรียนต่อวัน ได้หรือไม่ แสดงว่ามีแปรเกณฑ์  1  ตัวได้แก่ เงินที่บุตรได้ไปโรงเรียน  ตัวแปรทำนาย 2 ตัว ได้แก่ รายได้ของครอบครัว   และเกียรติภูมิในอาชีพของบิดา สามารถใช้โปรแกรม  SPSS for Windows  ได้ดังนี้

 

 

                       1ใช้คำสั่ง

            Analyze

                 Regression

                           Linear                     จะได้หน้าจอดังแสดงในรูปที่  3

              


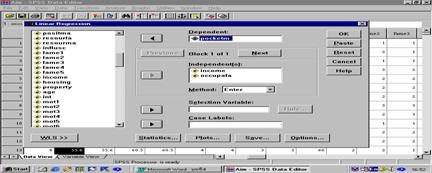
                                   รูปที่  3 Linear Regression

           

            จากรูปที่ 6  เลือกตัวแปรเกณฑ์  1  ตัว คือ เงินที่บุตรได้ไปโรงเรียน (pocketm) ใส่ใน box  ของ dependent  และเลือกตัวแปรทำนาย คือ รายได้ของครอบครัว(income) และเกียรติภูมิในอาชีพของบิดา (occupafa) ใส่ใน box ของ independent   ส่วนของ  method  เลือกenter

              2  เลือก        statistics       จะได้หน้าจอดังรูปที่ 4

 


รูปที่  4  Linear Regression : Statistics

 

            3. รูปที่ 4 ในส่วนของ Regression Coefficient   เลือก Estimates และ Confidence interval

                            ในส่วนของ Residuals  เลือก  Durbin-Watson

                            เลือก  Model fit , R square change , Part and  partial correlation และ Collinearity

                            diagostics

แล้วเลือก     continue     จะกลับมาหน้าจอเดิมรูปที่  6   เลือก      OK      จะได้ผลลัพธ์ในตารางที่ 6-10

ตารางที่ 5

ตารางที่6 เป็นตารางที่อธิบายถึงการเลือกตัวแปรอิสระเข้าสมการโดยวิธี enter โดยมีเงินที่บุตรได้ไปโรงเรียน (pocketm) เป็นตัวแปรตาม และตัวแปรอิสระที่นำเข้า คือ รายได้ของครอบครัว(income) และเกียรติภูมิในอาชีพของบิดา (occupafa)

 

ตารางที่ 6

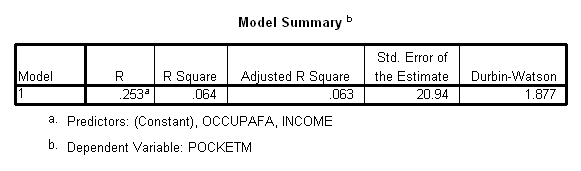
ตารางที่ 7  สรุปได้ดังนี้

R Square  = .064  คือค่าสัมประสิทธิ์การทำนาย เป็นสัดส่วนที่ตัวแปรอิสระสามารถอธิบายความผันแปรของตัวแปรได้มากน้อยเท่าไร  ในที่นี้แสดงว่ารายได้ของครอบครัว(income) และเกียรติภูมิในอาชีพของบิดา (occupafa) สามารถอธิบายความผันแปรของเงินที่บุตรได้ไปโรงเรียน (pocketm) ร้อยละ 6.4 ที่เหลืออธิบายได้ด้วยตัวแปรอื่น

สำหรับค่า Adjusted  R Square เป็นค่าที่มีการปรับให้ค่าสัมประสิทธิ์การทำนายมีความถูกต้องมากขึ้น เนื่องจากตัวแปรอิสระที่เพิ่มมากขึ้นในสมการถดถอย จะทำให้ค่า R Square เพิ่มขึ้นทั้งๆที่ตัวแปรอิสระที่เพิ่มมานั้นอาจไม่มีความสัมพันธ์กับตัวแปรตาม ดังนั้น จึงต้องมีการปรับสูตร R Square เพื่อลดปัญหาดังกล่าว

R เป็นค่าสัมประสิทธ์พหุคูณ ที่แสดงถึงความสัมพันธ์ระหว่างตัวแปรตามและชุดของตัวแปร

อิสระ  ในที่นี้มีค่าเท่ากับ .253  แสดงว่า เงินที่บุตรได้ไปโรงเรียน (pocketm)  กับ รายได้ของครอบครัว(income) และเกียรติภูมิในอาชีพของบิดา (occupafa) มีความสัมพันธ์กันไม่มากนัก 

Std Error of estimate เป็นค่าความคลาดเคลื่อนมาตรฐานของการประมาณค่าซึ่งเท่ากับ 20.94 บาท มีหน่วยเดียวกับตัวแปรตาม

Durbin-Watson เป็นค่าสถิติที่ทดสอบความเป็นอิสระของความคลาดเคลื่อน ซึ่งเป็นเงื่อนไขหนึ่งของการวิเคราะห์ถดถอย ในที่นี้ มีค่าเท่ากับ 1.877  ซึ่งมีค่าใกล้ 2 แสดงว่าค่าความคลาดเคลื่อนเป็นอิสระจากกัน

ตารางที่ 7

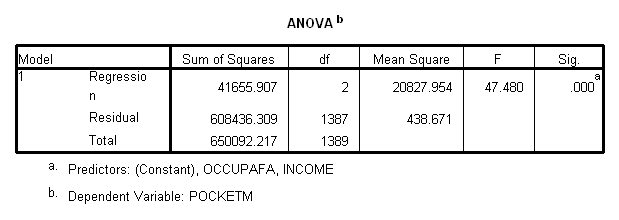
ตารางที่ 7  เป็นตารางวิเคราะห์ความแปรปรวนทางเดียว ซึ่งใช้ในการทดสอบสมมติฐาน

 H0 : b 1  = b 2  = 0

 H1 : b i  ¹0 อย่างน้อย 1 ตัว ; i =  1,2

ในที่นี้ ได้ค่าF = 47.480  Sig = .000   แสดงว่าปฏิเสธสมมติฐาน H0 สรุปได้ว่ามีตัวแปรอิสระอย่างน้อย 1 ตัวที่มีความสัมพันธ์เชิงทำนายตัวแปรตาม อย่างมีนัยสำคัญ จึงต้องทำการทดสอบต่อไปว่าตัวแปรอิสระใดบ้างที่มีความสัมพันธ์เชิงทำนาย เงินที่บุตรได้ไปโรงเรียน (pocketm) ในตารางที่ 9

 

 

ตารางที่ 8

 

 

Unstandardizes

Coefficients

Standardized

Coefficients

 

 

95 % Confidence

Interval  for B

Correations

Collinearity

Statistics

 

Model

B

Std. Error

Beta

t

Sig

Lower

Bound

Upper

Bound

Zero

order

Par

tial

part

tolerance

VIF

1 (Constant)

      income 

 

     occupafa

41.711

7.768 E-05

 

.317

2.842

.000

 

.054

 

.139

 

.165

14.678

4.962

 

5.877

.000

.000

 

.000

36.137

.000

 

.211

47.286

.000

 

.422

 

.202

 

.218

 

.132

 

.156

 

.129

 

.153

 

.856

 

.856

 

1.168

 

1.168

Dependent Variable : POCKETM

ตารางที่ 8 เป็นตารางที่แสดงการทดสอบความสัมพันธ์เชิงทำนายระหว่างตัวแปรตามกับตัวแปรอิสระที่ละตัว สรุปได้ ดังนี้

ใน Column   Unstandardized Coefficient  มีค่า B ซึ่งแสดงถึงค่าคงที่(a) และค่าสัมประสิทธิ์ถดถอย(b)  ส่วน Std  Error คือค่าความคลาดเคลื่อนมาตรฐานของค่า a และb  ในที่นี้ได้ค่าดังนี้

ค่าคงที่ a = 41.711 บาท        SE(a)  = 2.842

ค่าสัมประสิทธิ์ถดถอยของตัวแปรรายได้ของครอบครัว(income)(b1)=.000077 บาท

SE(b1)  =0

             ค่าสัมประสิทธิ์ถดถอยของตัวแปรเกียรติภูมิในอาชีพของบิดา (occupafa) b2 = .317 บาท         

            SE (b2 )    = .054  บาท

            ฺสมการถดถอยที่คาดไว้จะเป็น

                   ^

              POCKETM   = 41.711 + .000077 income + .317 occupafa

             จะต้องทดสอบต่อว่าเป็นจริงหรือไม่

 

ใน Column   Standardized Coefficient แสดงค่าสัมประสิทธิ์ถดถอยมาตรฐาน ซึ่งไม่มีหน่วย อยู่ในรูปของคะแนนมาตรฐาน (Z Score)

            ค่าสัมประสิทธิ์ถดถอยมาตรฐาน ของตัวแปรรายได้ของครอบครัว (income)  = .139

            ค่าสัมประสิทธิ์ถดถอยมาตรฐาน ของตัวแปรเกียรติภูมิในอาชีพของบิดา (occupafa) = .165

แสดงว่ามีความสัมพันธ์เชิงทำนายตัวแปรตาม คือ เงินที่บุตรได้ไปโรงเรียน

มากกว่ารายได้ของครอบครัว

โดยใช้ค่า t ทดสอบสมมติฐานเกี่ยวกับค่าคงที่และสัมประสิทธิ์ถดถอย   a  ,  b1   และ b2

ก. สมมติฐาน   H0 : a = 0  เป็นการทดสอบเกี่ยวกับค่าคงที่

                      H1 : a ¹0 

     สถิติทดสอบ    t = .14.678  Sig ของ  t = ..000  < .05  จึงปฏิเสธ  H0 หรือ a ¹0

ข. สมมติฐาน    H0 : b1    /  b2    =   0 

                       H1 : b1   /  b2     ¹ 0   หรือ

H0 : รายได้ของครอบครัว ไม่มีความสัมพันธ์เชิงทำนายเงินที่บุตรได้ไปโรงเรียนเมื่อกำหนดให้เกียรติภูมิในอาชีพของบิดาคงที่

H1 : รายได้ของครอบครัว มีความสัมพันธ์เชิงทำนายเงินที่บุตรได้ไปโรงเรียนเมื่อกำหนดให้เกียรติภูมิในอาชีพของบิดาคงที่

    สถิติทดสอบ  :  t = 4.962   Sig. ของสถิติทดสอบ t = .000   จึงปฏิเสธ H0 หรือ b1   /  b2     ¹ 0   นั่นคือ  รายได้ของครอบครัว มีความสัมพันธ์เชิงทำนายเงินที่บุตรได้ไปโรงเรียนเมื่อกำหนดให้เกียรติภูมิในอาชีพของบิดาคงที่

ค . สมมติฐาน    H0 : b2    /  b1   =   0 

                         H1 : b2    /  b1     ¹ 0   หรือ

H0 : เกียรติภูมิในอาชีพของบิดาไม่มีความสัมพันธ์เชิงทำนายเงินที่บุตรได้ไปโรงเรียน เมื่อกำหนดให้รายได้ของครอบครัว คงที่

H1 : เกียรติภูมิในอาชีพของบิดามีความสัมพันธ์เชิงทำนายเงินที่บุตรได้ไปโรงเรียนเมื่อกำหนดให้รายได้ของครอบครัว คงที่

สถิติทดสอบ  :  t = 5.877   Sig. ของสถิติทดสอบ t = .000   จึงปฏิเสธ H0 หรือ b2   /  b1     ¹ 0   นั่นคือ  เกียรติภูมิในอาชีพของบิดามีความสัมพันธ์เชิงทำนายเงินที่บุตรได้ไปโรงเรียน เมื่อกำหนดให้รายได้ของครอบครัว คงที่

สรุป  จากการทดสอบทั้งหมด สรุปได้ว่าตัวแปรอิสระทั้ง 2 ตัว คือรายได้ของครอบครัว และเกียรติภูมิในอาชีพของบิดามีความสัมพันธ์เชิงทำนายตัวแปรตาม คือเงินที่บุตรได้ไปโรงเรียนอย่างมีนัยสำคัญทางสถิติที่ระดับ 0.05

 ใน column   95 % Confidence   Interval  for B หมายถึง ค่าประมาณแบบช่วงของสัมประสิทธิ์ถดถอย   ที่ระดับความเชื่อมั่น 95 %

ใน column  Correlation มีค่าสัมประสิทธิ์สหสัมพันธ์แบ่งเป็น 3 ส่วน คือ

            1.  Zero –Order หมายถึง ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรตามกับตัวแปรอิสระแต่ละตัวโดยไม่ได้ควบคุมตัวแปรอิสระตัวอื่นๆ ในที่นี้ได้ค่าดังนี้

            ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปร pocketm กับ  income  =.202

            ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปร pocketm กับ  occupafa  = .218

แสดงว่าความสัมพันธ์ระหว่างเงินที่บุตรได้ไปโรงเรียนกับเกียรติภูมิในอาชีพของบิดามีมากกว่าความสัมพันธ์ระหว่างเงินที่บุตรได้ไปโรงเรียนกับรายได้ของครอบครัว

            2. Partial  หมายถึง ค่าสัมประสิทธิ์สหสัมพันธ์บางส่วนระหว่างตัวแปรตาม(y) กับตัวแปรอิสระแต่ละตัว(เช่น x1 )โดยได้ควบคุมตัวแปรอิสระตัวอื่นๆ (เช่น x2)ที่อาจจะสัมพันธ์กับตัวแปรตาม(y)  กับตัวแปรอิสระแต่ละตัว(x1 ) ในที่นี้ได้ค่าดังนี้

            ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปร pocketm กับ  income โดยควบคุมตัวแปร occupafaที่อาจจะสัมพันธ์กับ pocketm กับ income มีค่า = .132

            ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปร pocketm กับ  occupafa  โดยควบคุมตัวแปร incomeที่อาจจะสัมพันธ์กับ pocketm กับ occupafa มีค่า  = .156

            3. Part หมายถึง ค่าสัมประสิทธิ์สหสัมพันธ์บางส่วนระหว่างตัวแปรตาม(y) กับตัวแปรอิสระแต่ละตัว(เช่น x1 )โดยได้ควบคุมตัวแปรอิสระตัวอื่นๆ (เช่น x2)ที่อาจจะสัมพันธ์กับตัวแปรอิสระแต่ละตัว (x1 ) ในที่นี้ได้ค่าดังนี้

            ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปร pocketm กับ  income โดยควบคุมตัวแปร occupafaที่อาจจะสัมพันธ์ กับ income มีค่า = .129

            ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปร pocketm กับ  occupafa  โดยควบคุมตัวแปร incomeที่อาจจะสัมพันธ์กับ occupafa มีค่า  = .153

ใน column  Collinearity Statistics หมายถึง ค่าสถิติที่วัดความสัมพันธ์ของตัวแปรอิสระ

            Tolerance        =        1-R2                 

ถ้ามีค่าต่ำแสดงว่าตัวแปรอิสระตัวนั้นมีความสัมพันธ์กับตัวแปรอิสระตัวอื่นๆมาก

            VIF                  =    1/ 1-R2

ถ้ามีค่ามากแสดงว่าตัวแปรอิสระตัวนั้นมีความสัมพันธ์กับตัวแปรอิสระตัวอื่นๆมาก

ในที่นี้ได้ค่าดังนี้

Tolerance     ของ income และ occupafa   = .856    VIF  =  1.168

 

ตารางที่ 9

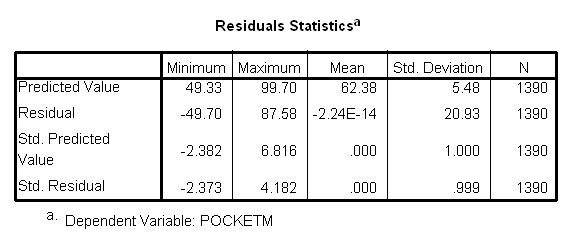ตารางที่ 9 เป็นตารางที่ให้ค่าสถิติองค่าคลาดเคลื่อน

Predicted Value หมายถึง  ค่าประมาณของตัวแปรตาม ในที่นี้คือค่าประมาณของเงินที่บุตรได้ไปโรงเรียน  หรือ Pock^etm  ที่มีค่าสูงสุด = 99.70     ต่ำสุด = 49.33

Residual หมายถึง ค่าความคลาดเคลื่อนที่เกิดจากการประมาณค่า Pocketm  ด้วย Pock^etmโดยที่              Residual   = Pocketm  - Pock^etm

Std. Predicted Value  หมายถึง   ค่าประมาณของตัวแปรตามในที่นี้คือค่าประมาณของเงินที่บุตรได้ไปโรงเรียน ในรูปคะแนนมาตรฐาน = Z poc^ketm

โดยที่                 Z poc^ketm         = Pock^etm  - mean (Pock^etm )

                                                                                                SD(Pock^etm )

 

Std. Residual  หมายถึง ถึง  ค่าความคลาดเคลื่อนมาตรฐาน  หรือ   Z Residual

                           Z Residual    = Residual - mean (Residual)

                                                                                                SD( Residual)

               สรุป  จากการวิเคราะห์สมการถดถอยของตัวแปรเงินที่บุตรได้ไปโรงเรียน กับรายได้ของครอบครัวและเกียรติภูมิในอาชีพบิดานั้น พบว่าตัวแปรอิสระทั้ง 2 ตัว มีความสัมพันธ์เชิงทำนายกับตัวแปรตามอย่างมีนัยสำคัญทางสถิติ และสามารถเขียนสมการในรูปของคะแนนดิบและในรูปของคะแนนมาตรฐานได้ ดังนี้

สมการในรูปของคะแนนดิบ

                          ^

                 POCK ETM   =     41.711 + .000077 income + .317 occupafa

 

            สมการในรูปของคะแนนมาตรฐาน

                   Z poc^ketm =     .139 Z income + .165 Z occupafa

 

 

แบบฝึกหัด

1.      จงระบุสถิติที่ใช้ในการหาความสัมพันธ์ของตัวแปรต่อไปนี้

1.1  การหาความสัมพันธ์ระหว่างอันดับที่ของภาพวาดจากกรรมการ 2 ท่าน

1.2  การหาความสัมพันธ์ระหว่างคะแนนภาวะผู้นำกับการเป็นที่ยอมรับของผู้ใต้บังคับบัญชา

1.3  การหาความสัมพันธ์ระหว่างการไปเลือกตั้งกับระดับการศึกษา

1.4  การหาความสัมพันธ์ระหว่างการชอบเล่นฟุตบอลกับการชอบดูฟุตบอล

1.5  การหาความสัมพันธ์ระหว่างเพศกับการเรียนต่อต่างประเทศ

2.      จงหาความสัมพันธ์ระหว่างส่วนสูงกับน้ำหนักของนิสิต 5 คนจากข้อมูลต่อไปนี้ พร้อมแปลความหมายและทดสอบนัยสำคัญของค่าสหสัมพันธ์ดังกล่าว ที่ระดับนัยสำคัญที่0.05

 

นิสิต

ส่วนสูง

น้ำหนัก

1

2

3

4

5

160

170

165

148

155

49

60

55

40

50

 

3.      จงหาความสัมพันธ์ระหว่างการกวดวิชากับคะแนนสอบเข้ามหาวิทยาลัยของนิสิต 10 คน จากข้อมูลที่กำหนดพร้อมทั้งแปลความหมาย

นิสิตคนที่

1

2

3

4

5

6

7

8

9

10

กวดวิชา

1

1

1

1

1

0

0

0

0

0

คะแนน

300

250

275

190

400

200

150

210

305

175

 

4. นักวิจัยต้องการศึกษาว่าทัศนคติต่อวิชาสถิติจะทำนายคะแนนวิชาสถิติได้หรือไม่ จึงสุ่มตัวอย่างนิสิตมา 10 คน เก็บข้อมูลทัศนคติต่อวิชาสถิติและคะแนนสถิติ ได้ดังนี้

 

นิสิตคนที่

1

2

3

4

5

6

7

8

9

10

ทัศนคติ

10

8

8

3

4

5

7

8

9

4

คะแนน

7

8

7

5

6

3

9

5

6

3

จงสร้างสมการทำนายทั้งคะแนนดิบและคะแนนมาตรฐาน พร้อมทดสอบนัยสำคัญของ

สัมประสิทธิ์การถดถอย

5. นักการศึกษาต้องการศึกษาว่าผลสัมฤทธิ์ทางการเรียนของนิสิตมีความสัมพันธ์กับแรงจูงใจใฝ่สัมฤทธิ์ของนิสิตและอายุของนิสิตหรือไม่ จึงเก็บข้อมูลกับนิสิต 15 คน ได้ข้อมูล ดังนี้

 

นิสิต

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

แรงจูงใจ

8

10

12

15

18

20

18

16

14

12

10

18

17

16

15

อายุ

20

22

24

26

28

30

28

26

22

24

22

25

25

24

26

คะแนน

70

82

83

85

84

90

87

84

81

82

79

81

84

82

86

 

5.1 จงเขียนสมการถดถอยแสดงความสัมพันธ์ระหว่างผลสัมฤทธิ์ทางการเรียน  แรงจูงใจใฝ่สัมฤทธิ์ของนิสิตและอายุของนิสิต

5.2 จงทดสอบความสัมพันธ์ในข้อ5.1 ที่ระดับนัยสำคัญที่ 0.05

5.3 จงหาค่าสัมประสิทธิ์การทำนายพร้อมทั้งอธิบายความหมาย