บทที่ 5

การประยุกต์ใช้ Non parametric statistics บางประการสำหรับงานวิจัย

Non parametric statistics ที่นำมาใช้เพื่อในการวิเคราะห์ข้อมูลจำแนกประเภท หรือนับความถี่

ของแต่ละระดับหรือของแต่ละกลุ่ม คือไคสแควร์ (c²) การทดสอบไคสแควร์มีหลายรูปแบบ

แต่ในที่นี้จะแยกเป็นดังนี้

1. การทดสอบสมมติฐานสำหรับข้อมูลที่จำแนกทางเดียว แบ่งเป็น

1.1 การทดสอบความแตกต่างระหว่างความถี่

1.2 การทดสอบสัดส่วนประชากรว่าเท่ากับที่คาดหวังหรือไม่

1.3 การทดสอบการแจกแจงของประชากรว่าเป็นไปตามที่คาดหวังหรือไม่(Goodness of fit)

2. การทดสอบสมมติฐานสำหรับข้อมูลที่จำแนกสองทาง

2.1 การทดสอบความเป็นอิสระกันระหว่างลักษณะ 2 ลักษณะ(ความสัมพันธ์ระหว่าง 2 ตัว)

1. การทดสอบสมมติฐานสำหรับข้อมูลที่จำแนกทางเดียว ลักษณะของข้อมูลที่จำแนกทางเดียว คือเป็นข้อมูลที่จำแนกตามลักษณะใดลักษณะหนึ่งเพียงลักษณะเดียว เช่น จำแนกคนตามระดับการศึกษาสูงสุด เช่น ต่ำกว่ามัธยมศึกษาตอนปลาย มัธยมศึกษาตอนปลาย ปริญญาตรีหรืออนุปริญญา สูงกว่าปริญญาตรี การทดสอบสมมติฐานสำหรับข้อมูลที่จำแนกทางเดียวดังกล่าว สามารถทดสอบสมมติฐานโดยใช้สถิติไคสแควร์ (c²) โดยมีข้อตกลงเบื้องต้น ดังนี้

ข้อตกลงเบื้องต้นของ c² - test

1. ข้อมูลแต่ละค่าจะต้องอยู่ที่ cell ใด cell หนึ่ง เท่านั้น

2. ข้อมูลแต่ละค่าจะเป็นอิสระจากข้อมูลอื่น

3. ข้อมูลที่นำมาวิเคราะห์จะเป็นค่าความถี่

4. ค่าความถี่คาดหวังในแต่ละ Cell จะต้องไม่น้อยกว่า 5 สำหรับ กรณีที่ df ³ 2 และไม่น้อยกว่า 10 ถ้า df = 1

ทดสอบสมมติฐานโดยใช้สถิติไคสแควร์ (c²)ในที่นี้จะสรุปเป็น 3 ลักษณะ คือการทดสอบความแตกต่างระหว่างความถี่ การทดสอบสัดส่วนประชากรว่าเท่ากับที่คาดหวังหรือไม่ และการทดสอบการแจกแจงของประชากรว่าเท่ากับที่คาดหวังหรือไม่ (Goodness of fit) โดยมีรายละเอียดดังนี้

1.1 การทดสอบความแตกต่างระหว่างความถี่ การทดสอบแบบนี้จะมีตัวแปรที่ต้องการวิเคราะห์มีเพียงตัวเดียว แต่แบ่งเป็นหลายประเภท และทดสอบว่า ความถี่ที่เกิดขึ้นในแต่ละประเภทเท่ากันหรือไม่ หรือทดสอบว่าความถี่ที่เกิดขึ้นเท่ากับความถี่ที่กำหนดหรือไม่ โดยมีสมมติฐาน คือ

H ₀ : P₁ = P₂ =… P_k = 1/k

H ₁ : P_i : _¹ 1/k อย่างน้อย 1 ค่า I = 1 , 2 ,… k

โดยมีสถิติที่ใช้ในการทดสอบ คือ

n

c ² = å ( O_i- E _i ) ²

i=1 E _i

เมื่อ c ² = สัญลักษณ์ของไคส์แควร์

O = ความถี่ที่แจงนับได้

E = ความถี่ที่คาดหวังหรือที่กำหนด

n = จำนวนตัวอย่างทั้งหมด

เขตปฏิเสธ จะปฏิเสธ H ₀ เมื่อ c ² > c ²_{(1 - a ) : k-1}

ตัวอย่าง ในโรงเรียนแห่งหนึ่งได้ให้นักเรียน100 คน เลือกครูภาษาไทยดีเด่นในโรงเรียน ซึ่งมี ครูภาษาไทยอยู่ 5 คน คือครู ก ครู ข ครู ค ครู ง และครู จ โดยที่ผู้อำนวยการโรงเรียนต้องการทราบว่าครู จ ซึ่งเป็นครูใหม่ จะได้รับการเลือกจากนักเรียนแตกต่างจากครูเก่าหรือไม่

การคำนวณ ถ้าครู ได้รับการเลือกจากนักเรียนเท่าๆกัน จะต้องได้รับการคัดเลือก คนละ 20 เสียง

สามารถคำนวณหาค่า c ² ได้ดังนี้

ครู	O	E	O- E	(O- E)^2	(O- E)^2/E
ก ข ค ง จ	17 27 22 15 19	20 20 20 20 20	-3 7 2 -5 -1	9 49 4 25 1	.45 2.45 .20 1.25 .05
รวม	100	100	0		4.40

n

c ² = å ( O_i- E _i ) ²

i=1 E _i

= 4.40

เขตปฏิเสธ จะปฏิเสธ H ₀ เมื่อ c ² > c ² _{a : k-1} ที่องศาอิสระ 5-1 = 4 จากการเปิดตาราง c ² ได้c ²_{(0.95: 4)} =9.49 ซึ่งมากกว่า 4.4 จึงไม่สามารถปฏิเสธ H ₀ นั่นคือยอมรับ H ₀ คือ ครูได้รับการเลือกจากนักเรียนไม่แตกต่างกันอย่างมีนัยสำคัญทางสถิติที่ระดับ 0.05

1.2 การทดสอบสัดส่วนประชากรว่าเท่ากับที่คาดหวังหรือไม่ การทดสอบแบบนี้จะมีตัวแปรที่ต้องการวิเคราะห์มีเพียงตัวเดียว แต่แบ่งเป็นหลายประเภท และทดสอบว่าสัดส่วนที่เกิดขึ้นเท่ากับสัดส่วนที่กำหนดหรือไม่ โดยมีสมมติฐาน คือ

H ₀ : P₁ : P₂ … : P_k = P₁₀ : P₂₀ … : P_k0

H ₁ : P_i ¹ P_i0 อย่างน้อย 1 ค่า ; i = 1, 2 ,…k

โดยที่ P_i0 = สัดส่วนที่คาดว่าจะเป็น ซึ่งเป็นค่าคงที่ อยู่ระหว่าง 0 – 1

สถิติที่ใช้ทดสอบคือ n

c ² = å ( O_i- E _i ) ²

i=1 E _i

เมื่อ c ² = สัญลักษณ์ของไคสแควร์

O = ความถี่ที่แจงนับได้

E = ความถี่ที่คาดหวังหรือที่กำหนด

n = จำนวน

สูตรคำนวณ E = n p_i0

เขตปฏิเสธ จะปฏิเสธ H ₀ เมื่อ c ² > c ² _{a : k-1}

ตัวอย่าง ยาแก้ปวดศีรษะชนิดหนึ่ง บริษัทอ้างว่ารักษาผู้ป่วยหายภายใน 3 ชั่วโมง ร้อยละ 90 เพื่อทดสอบสรรพคุณของยาชนิดนี้ จึงเลือกผู้ป่วยมา 400 คน และให้กินยาดังกล่าวพบว่าหายภายใน 3 ชั่วโมง 320 คนยาชนิดนี้สรรพคุณตามที่อ้างหรือไม่

การคำนวณ ถ้ายานี้มีสรรพคุณที่อ้างผู้ป่วย 100 คน จะต้องหาย 90 ฉะนั้นถ้าทดลองกับผู้ป่วย 400 คน จะต้องหาย 360 คน และไม่หาย 40 คน จากหลักการนี้สามารถคำนวณหาค่าไคสแควร์ ดังนี้

สมมติฐาน สัดส่วนการหายปวด : ไม่หายปวด = 90 : 10

หรือ H ₀ : P₁ : P₂ = 90 : 10

H ₁ : P₁ : P_{2 ¹} 90 : 10

E = n p

ตารางการวิเคราะห์ไคสแควร์

ผลการทดลอง	O	E	O -E	( O -E ) ^2	( O -E ) ^2/ E
หาย	320	360	- 40	1600	4.44
ไม่หาย	80	40	40	1600	40.00
รวม	400	400	0		44.44

ฉะนั้น c ² = 44.44 นำไปเปรียบเทียบกับค่า c ² ในตาราง df = 2-1 = 1 และ a =0.05 =3.84 แสดงว่าค่า c ² ที่คำนวณได้มากกว่าค่าในตาราง หมายความว่า ยานี้ให้ผลต่างจากร้อยละ 90 นั้น คือ ไม่มีสรรพคุณตามที่อ้างไว้

อนึ่ง ในการคำนวณค่า c ² ถ้า df = 1หรือ ค่า E น้อยกว่า 5 ควรปรับสูตรด้วยการเอา 0.5 ลบออกจากผลที่ได้ไม่ติดเครื่องหมายก่อนแล้วจึงยกกำลังสองจึงจะทำให้ค่า c ² ที่ได้ตรงกับความเป็นจริงมากขึ้น สูตรก็เป็น

c ² = å (÷ O -Eô- 0.5) ²

E

1.3 การทดสอบการแจกแจงของประชากรว่าเป็นไปตามที่คาดหวังหรือไม่ การทดสอบแบบนี้จะมีตัวแปรที่ต้องการวิเคราะห์มีเพียงตัวเดียว แต่แบ่งเป็นหลายประเภท และทดสอบว่าสัดส่วนที่เกิดขึ้นเท่ากับสัดส่วนตามการแจกแจงตามที่คาดหวังหรือไม่ ยังคงเรียกว่าการทดสอบภาวะรูปสนิทดี (Goodness of fit)การแจกแจงที่คาดไว้อาจเป็นการแจกแจงแบบต่อเนื่อง เช่นการแจกแจงแบบปกติ หรือการแจกแจงแบบไม่ต่อเนื่อง เช่นการแจกแจงแบบทวินามหรือการแจกแจงแบบปัวซอง โดยมีสมมติฐาน คือ

H ₀ : ประชากรมีการแจกแจงแบบ Y

H ₁ : ประชากรไม่ได้มีการแจกแจงแบบ Y

โดยที่ Y อาจเป็นแบบปกติ ทวินามหรือปัวซอง

สถิติที่ใช้ทดสอบคือ n

c ² = å ( O_i- E _i ) ²

i=1 E _i

เมื่อ c ² = สัญลักษณ์ของไคส์แควร์

O = ความถี่ที่แจงนับได้

E = ความถี่ที่คาดหวังหรือที่กำหนด

n = จำนวน

สูตรคำนวณ E = n ´ ความน่าจะเป็นที่จะเกิดขึ้นในลักษณะที่ i ของการแจกแจงที่คาดไว้

โดยที่ c ² มีการแจกแจงแบบไคสแควร์ที่องศาอิสระ (k-1)-m

m คือจำนวนพารามิเตอร์ที่ต้องประมาณค่า จะมีค่าเท่าไรขึ้นอยู่กับการแจกแจงที่คาดไว้ที่ต้องการทดสอบ เช่น ถ้าสมมติฐาน คือ H ₀ : ประชากรมีการแจกแจงแบบปกติ

m = 2 เนื่องจากต้องประมาณค่าเฉลี่ยและค่าความแปรปรวน c ² ~ c ²_(k-1-2)

ถ้าสมมติฐาน คือ H ₀ : ประชากรมีการแจกแจงแบบปกติด้วยค่าเฉลี่ย = 5 ค่าความแปรปรวน = 6

m = 0 เนื่องจากไม่ต้องประมาณค่าเฉลี่ย (m)และค่าความแปรปรวน(s²) c ² ~ c ²_(k-1)

ตัวอย่าง จากการถามคนไทยในเขตหนองจอก จำนวน 83 คน ถึงรายได้ต่อเดือน ปรากฏว่าได้ข้อมูล ดังนี้

รายได้ต่อเดือน(หน่วย:100,000 บาท	จำนวน (คน)
น้อยกว่า .1 .1แต่น้อยกว่า .15 .15 แต่น้อยกว่า .20 .20 แต่น้อยกว่า .25 ตั้งแต่ .25 ขึ้นไป รวม	12 20 23 15 13 83

จงทดสอบว่ารายได้ของคนในเขตหนองจอก มีการแจกแจงปกติด้วยรายได้เฉลี่ย 20,000บาทต่อเดือน ค่าเบี่ยงเบนมาตรฐาน 5,000 บาทต่อเดือนที่ระดับความเชื่อมั่น 99%

สมมติฐานเพื่อการทดสอบ คือ

H ₀ : รายได้ของคนหนองจอกมีการแจกแจงแบบปกติด้วยรายได้เฉลี่ย 20,000 บาท ส่วนเบี่ยงเบน

มาตรฐาน 5,000 บาท

H ₁ : รายได้ของคนหนองจอกไม่มีการแจกแจงแบบปกติด้วยรายได้เฉลี่ย 20,000 บาท ส่วนเบี่ยงเบนมาตรฐาน 5,000 บาท

สถิติที่ใช้ทดสอบคือ

n

c ² = å ( O_i- E _i ) ²

i=1 E _i

เมื่อ O₁ = 12 , O₂ = 20 , O₃ = 23 , O₄ = 15 , O₅ = 13

ให้ x = รายได้ต่อเดือนของคนในเขตหนองจอก

คำนวณหาค่า E ได้ดังนี้

เมื่อ H ₀ จริง E = np

โดยที่ p = ความน่าจะเป็นที่คนในเขตหนอกจอกมีรายได้ในช่วงที่ i ; i =1,2,3,4,5

นั่นคือคำนวณค่า p เมื่อ x ~ normal ((m= .2 ,s= .05) ดังแสดงในรูป

รูปหน้า 191 กัลยาน้ำเงิน

เปลี่ยน x เป็นz โดยที่ z = x - m /s = x - .2 / .05 ได้ค่า z และหาค่า E ได้ดังตาราง ดังนี้

ช่วงที่	รายได้(x)	z = x - .2 / .05	p	E= 83p	O
1 2 3 4 5	x < .1 .1< x < .15 .15 < x < .2 .2 < x < .25 x ³ .25	.1 - .2 / .05 = - 2 .15 - .2 / .05 = - 1 .2 - .2 / .05 = 0 .25 - .2 / .05 = 1	.0228 .1359 .3413 .3413 .1587	1.89 11.28 28.33 28.33 13.17	12 20 23 15 13

เนื่องจากE₁ = 1.89 น้อยกว่า 5 จึงรวมรายได้ช่วงที่ 1 และช่วงที่2 เข้าด้วยกัน ดังนั้นจำนวนช่วงจึงเหลือ 4 และ O₁ = 12+20 =32 E₁= 1.89+11.28 = 13.17

c ² = å ( O- E ) ²

E

= (32-13.17)² +(23-28.33)² +(15-28.33)² +(13-13.17)²

13.17 28.33 28.33 13.17

= 34.20

เขตปฏิเสธ จะปฏิเสธ H ₀ เมื่อ c ² > c ²_{.01 : 4-1} จากการเปิดตาราง c ² ได้c ²_{.01 : 3} = 11.34 ดังนั้นจึงปฏิเสธ H ₀ นั่นคือ รายได้ต่อเดือนของคนในเขตหนองจอกไม่ได้มีการแจกแจงแบบปกติ ที่มีค่าเฉลี่ย = 20,000 บาท ค่าเบี่ยงเบนมาตรฐาน = 5,000 บาทอย่างมีนัยสำคัญทางสถิติที่ระดับ 0.01

สำหรับการทดสอบการแจกแจงลักษณะอื่นๆก็มีวิธีการหาเช่นเดียวกัน

2. การทดสอบสมมติฐานสำหรับข้อมูลที่จำแนกสองทาง

2.1 การทดสอบความเป็นอิสระกันระหว่างลักษณะ 2 ลักษณะ (ความสัมพันธ์ระหว่าง 2 ตัวแปร)

กรณีนี้จะมีตัวแปร 2 ตัว ระดับการวัดเป็นนามบัญญัติ ( Nominal scale ) ทั้งคู่ โดยใช้ตารางจำแนกแบบ 2 ทาง คือแนวตั้งและแนวนอน ตัวอย่าง เช่น เพศกับผลการเรียนเป็นอิสระกันหรือไม่ โดยที่เพศ แบ่งเป็น 2 กลุ่ม คือ ชาย และหญิง ส่วนผลการเรียนแบ่งเป็น ดี ปานกลาง อ่อน เป็นต้น

สถิติที่ใช้คงเป็น c ² โดยมีสมมติฐาน คือ

H ₀ : ลักษณะหรือตัวแปรทั้งสองเป็นอิสระกัน

H ₁ : ลักษณะหรือตัวแปรทั้งสองไม่เป็นอิสระกัน

สถิติที่ใช้ทดสอบคือ

c ² = å ( O- E ) ²

E

โดยที่ E = R ´ C

N

เมื่อ R = ผลรวมของความถี่ในแถวนอน

C = ผลรวมของความถี่ในแนวตั้ง

N = ผลรวมของความถี่ทั้งหมด

เขตปฏิเสธ จะปฏิเสธ H ₀ เมื่อ c ² > c ²_{a : ( r- 1 ) ( c - 1)} ด้วยองศาอิสระ (r-1)(c-1)

ตัวอย่าง จากการศึกษาจำนวนนักศึกษาที่มีความเชื่อโชคลาง จำแนกตามประเภทนักศึกษา

ประเภทนักศึกษา เชื่อ ไม่แน่ใจ ไม่เชื่อ รวม

วิทยาศาสตร์ 5 45 50 100

แพทยศาสตร์ 25 55 20 100

รัฐศาสตร์ 40 40 20 100

อักษรศาสตร์ 45 25 30 100

สังคมศาสตร์ 35 35 30 100

รวม 150 200 150 500

จากตาราง หาความถี่ที่คาดหวัง ( E ) ของแต่ละประเภทได้ด้วยสูตร

E = R ´ C

N

เมื่อ R = ผลรวมของความถี่ในแถวนอน

C = ผลรวมของความถี่ในแนวตั้ง

N = ผลรวมของความถี่ทั้งหมด

เช่น แถวนอน เมื่อ O = 5 , E = 100 X150 = 30

500

ทำนองเดียวกันจะคำนวณค่า E ของทุกประเภทได้ ซึ่งจะได้ตาราง

ตาราง จำนวนนักศึกษาที่คาดว่าจะเชื่อโชคลาง จำแนกตามประเภทของนักศึกษา

เชื่อ ไม่แน่ใจ ไม่เชื่อ

O E O E O E

วิทยาศาสตร์ 5 30 45 40 50 30

แพทย์ศาสตร์ 25 30 55 40 20 30

รัฐศาสตร์ 40 30 40 40 20 30

อักษรศาสตร์ 45 30 25 40 30 30

สังคมศาสตร์ 35 30 35 40 30 30

จากตาราง ก็จะหาค่า c ² ได้ด้วยการแทนค่าในสูตรดังนี้

c ²= ( 5 - 30 ) ² + ( 25 - 30 ) ² + ( 40 - 30 ) ² + ( 45 - 30 ) ² + ( 35 - 30 ) ²

30 30 30 30 30

= 65.83

การแปลความหมายจะต้องนำค่า c ² ที่คำนวณได้ไปเปรียบเทียบกับ ค่า c ² ในตาราง

df = ( r - 1 ) ( c -1 ) = ( 3 - 1 ) ( 5 - 1 ) = 8 และµ ที่กำหนด คือ 0.05 หรือ 0.01 หรือ 0.001 ถ้ากำหนด = 0.05 ค่า c ²ในตารางจะได้ 15.51 ซึ่งค่าที่คำนวณได้มากกว่า แสดงว่าการเชื่อโชคลางไม่เป็นอิสระจากประเภทของนักศึกษา หรือการเชื่อโชคลางมีความสัมพันธ์กับประเภทของนักศึกษา แต่ยังไม่ทราบว่าประเภทใดกับประเภทใดสัมพันธ์กันบ้างจะต้องวิเคราะห์รายคู่ต่อไป ด้วยการจับนักศึกษาแต่ละประเภท

เปรียบเทียบกันทีละคู่ ๆ หาค่า E ใหม่ และแทนค่าในสูตรเดิม เช่น คู่วิทยาศาสตร์กับแพทย์ศาสตร์ ก็จะได้ดังตาราง

ตาราง จำนวนนักศึกษาที่เชื่อและคาดว่าจะเชื่อโชคลางจำแนกตามประเภทของนักศึกษา

เชื่อ ไม่แน่ใจ ไม่เชื่อ

O E O E O E

วิทยาศาสตร์ 5 15 45 50 50 35

แพทยศาสตร์ 25 15 55 50 20 35

สำหรับการทดสอบสมมติฐาน c ² ที่ทดสอบความสัมพันธ์ของตัวแปรหรือทดสอบความเป็นอิสระของตัวแปร โดยใช้โปรแกรม SPSS for Windows มีรายละเอียด ดังนี้

การทดสอบ c ² โดยใช้โปรแกรม SPSS for Windows

การทดสอบc ² สามารถการวิเคราะห์ โดยใช้โปรแกรม SPSS for Windows มีวิธีการ ดังนี้

1 ) อธิบายความสัมพันธ์ระหว่างตัวแปร

1 . ความสัมพันธ์ระหว่างตัวแปร 2 ตัว ที่มีระดับการวัดเป็น nominal ( ใช้สถิติ c ²)

1.1 ใช้คำสั่ง

Analyze

Descriptive Statistics จะได้หน้าจอดังรูปที่ 1

Crosstabs

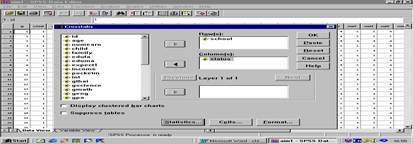
รูปที่ 1

จากรูปที่ 1 - เลือกตัวแปรที่มีการวัดระดับ nominal ที่ต้องการใส่ใน Box ของ Row และ Column

1.2

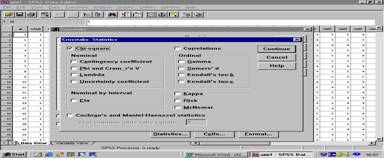
เลือก statistics จะได้หน้าจอดังรูปที่ 2

รูปที่ 2

จากรูปที่ 2 เลือก chi - square แล้วเลือก continue จะกลับไปหน้าจอรูปที่ 1

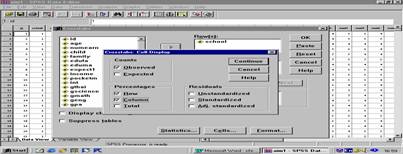
1.3 เลือก cells จะได้หน้าจอดังรูปที่ 3

รูปที่ 3

จากรูปที่ 3 สามารถเลือก counts , percentages และ Residuals เมื่อ เลือกแล้วเลือก continue จะกลับไปหน้าจอรูปที่ 1

1.4 เลือก Format….. จะได้หน้าจอ ดังรูปที่ 4

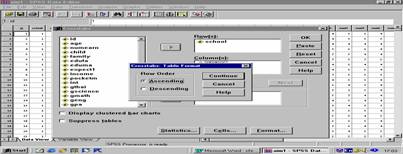
รูปที่ 4

จาก รูปที่ 4 เลือก Row Order

- Ascending แสดงตัวแปร row ตามค่าที่เรียงจากน้อยไปมาก

- Descending แสดงตัวแปร row ตามค่าที่เรียงจากมากไปน้อย

เลือก continue จะกลับมาหน้าจอรูปที่ 1 เลือก OK จะได้ผลลัพธ์แสดงในตารางที่ 1-2

ตารางที่ 1 School * Status of parent Crosstabulation

	‚ status of parent				…
Œ	1 (คู่)	2 (หม้าย)	3(หย่า)	4 (แยก)	Total
School 1 Count % within school % within status % of Total	306 ƒ 95.3 % 24.3% 21.5%	5 1.6% 8.9% 0.4%	5 1.6% 9.1% 0.4%	5 1.6% 9.3% 0.4%	321 100.0% 22.5% 22.5%
School 2 Count % within school % within status % of Total	431 88.1 % 34.2% 30.2%	17 3.5 % 30.4% 1.2%	20 4.1 % 36.4% 1.4%	21 4.3 % 38.9% 1.5%	489 100.0 % 34.3% 34.3%
School 3 Count % within school % within status % of Total	265 84.1 % 21.0% 18.6%	22 7.0 % 39.3% 1.5%	13 4.1 % 23.6% 0.9%	15 4.8 % 27.8% 1.1%	315 100.0 % 22.1% 22.1%
School 4 Count % within school 4 % within status % of Total	288 86 % 20.5% 18.1%	12 4.0% 21.4% 0.8%	17 5.7% 30.9% 1.2%	13 4.3% 24.1% 0.9%	300 100% 21.1% 21.1%
School total Count % within school % within status % of Total	1260 88.4 % 100% 88.4%	56 3.9 % 100% 3.9%	55 3.9 % 100% 3.9%	54 3.8 % 100% 3.8%	1425 100 % 100% 100%

ตารางที่ 2 Chi -Square Tests

	Value	df	Asymp Sig ( 2-sided )
Pearson Chi-Square † Likelihood Ratio ‡ Linear – by – Linear Associationˆ N of Vaild Cases	27.565^a 29.612 12.104 1425	9 9 1	.001 .001 .001

‰ a. 0 cells ( 0% ) have expected count less than 5. The minimum expected count is 11.37

ความหมายของผลลัพธ์ในตารางที่ 1

1	แสดง label ของตัวแปรทางด้าน row คือ school ซึ่งแบ่งเป็น 4ประเภท คือ 1 2 3 และ 4
2	แสดง label ของตัวแปรทางด้าน column คือ status ซึ่งแบ่งเป็น 4 ประเภท คือ 1 (คู่) 2 (หม้าย) 3 (หย่า) และ4 (แยก)
3	แสดงจำนวน และเปอร์เซ็นต์ของสถานภาพสมรสคู่ ดังนี้ - ผู้ปกครองมีสถานภาพสมรสคู่ 306 คน ( Observed) - มีผู้ปกครองของนักเรียนที่เรียนอยู่ในโรงเรียน ประเภท1 มีสถานภาพสมรสคู่ 95.3 % ของจำนวนนักเรียนที่เรียนอยู่ในโรงเรียนประเภท 1 ทั้งหมด ( 306/321 :Row Percent ) - มีผู้ปกครองของนักเรียนที่เรียนอยู่ในโรงเรียน ประเภท1 มีสถานภาพสมรสคู่ 24.3 % ของผู้ปกครองที่มีสถานภาพสมรสคู่ทั้งหมด ( 306/1260 %:column percent ) - มีผู้ปกครองของนักเรียนที่เรียนอยู่ในโรงเรียน ประเภท1 มีสถานภาพสมรสคู่ 21.5 % ของตัวอย่างทั้งหมด ( 306/1425 : Total percent ) - ใน cell อื่น ๆ ก็มีความหมายในลักษณะเดียวกัน
4	แสดงความถี่และเปอร์เซ็นต์รวมของแต่ละสถานภาพสมรส เช่น - มีผู้ปกครองมีสถานภาพสมรสคู่ 1260 ครอบครัว จากตัวอย่างทั้งหมด 1425 ครอบครัว หรือคิดเป็น 84.1 % ของตัวอย่างทั้งหมด - มีผู้ปกครองมีสถานภาพสมรสหย่า 55 ครอบครัว จากตัวอย่างทั้งหมด 1425 ครอบครัว หรือคิดเป็น3.9 % ของตัวอย่างทั้งหมด
5	แสดงความถี่และเปอร์เซ็นต์รวมของแต่ละเพศ เช่น - มีนักเรียนจากโรงเรียนประเภท 1 321 คน จากตัวอย่างทั้งหมด 1425 คน หรือคิดเป็น 22.5 % ของตัวอย่างทั้งหมด - มีนักเรียนจากโรงเรียนประเภท 2 489 คน จากตัวอย่างทั้งหมด 1425 คน หรือคิดเป็น 34.3 % ของตัวอย่างทั้งหมด

ความหมายของผลลัพธ์ในตารางที่ 2

6	H0 : ประเภทของโรงเรียน และสถานภาพสมรสของผู้ปกครองเป็นอิสระกัน H1 : ประเภทของโรงเรียน และสถานภาพสมรสของผู้ปกครองมีความสัมพันธ์กัน กำหนดระดับนั้นสำคัญ = .05 สถิติทดสอบ Pearson Chi - Square = 27.565 ที่องศาอิสระ 9 และ ได้ค่า Significance ของการทดสอบ = .001 ซึ่งน้อยกว่ากว่าระดับนัยสำคัญที่กำหนด ( .05 ) จึงปฏิเสธ H0 นั้นคือประเภทของโรงเรียน และสถานภาพสมรสของผู้ปกครองมีความสัมพันธ์กัน
7	สถิติทดสอบ Likelihood Ratio Chi-Square =29.612 องศาอิสระ = 9 Singnificance = .001 จึงสรุปว่าประเภทของโรงเรียน และสถานภาพสมรสของผู้ปกครองมีความสัมพันธ์กัน
8	สถิติทดสอบ Linear - by - Lienar Association Chi-Square ที่ใช้ทดสอบสมมติฐาน H0 : ประเภทของโรงเรียน และสถานภาพสมรสของผู้ปกครองไม่มีความสัมพันธ์กันในรูปเชิงเส้น H1 : ประเภทของโรงเรียน และสถานภาพสมรสของผู้ปกครองมีความสัมพันธ์กันในรูปเชิงเส้น ได้ค่าสถิติทดสอบ =.12.104 ที่องศาอิสระ = 1และค่า Significance = .001 จึงสรุปได้ว่าประเภทของโรงเรียน และสถานภาพสมรสของผู้ปกครองมีความสัมพันธ์กันในรูปเชิงเส้น
9	ระบุจำนวน cell ที่มีความถี่ที่คาดไว้ < 5 ในที่นี้ไม่มีcell ที่มีความถี่ที่คาดไว้ต่ำกว่า5 เลย ความถี่ที่ต่ำสุดใน cell =11.37

แบบฝึกหัด

1. ทางฝ่ายการศึกษาของสถาบันการศึกษาแห่งหนึ่งต้องการทดสอบความสัมพันธ์ระหว่างเพศของอาจารย์กับสถานศึกษาที่อาจารย์จบ ที่ระดับนัยสำคัญ .05 จึงสุ่มอาจารย์ในสถาบันมา 84 คน แยกตามเพศและสถานศึกษาที่อาจารย์จบ ดังนี้

เพศ	สถานศึกษาที่อาจารย์จบ
	ในประเทศ	ต่างประเทศ	ทั้งในและต่างประเทศ
ชาย	12	6	13
หญิง	19	16	18

2. บริษัทขายคอมพิวเตอร์แห่งหนึ่งได้เก็บข้อมูลของลูกค้าในปีที่ผ่านมา ดังนี้

บริษัทเอกชน 69 % รัฐบาล 21 % ฝ่ายการศึกษา 7 % บ้านอยู่อาศัย 3 %

ทางบริษัทต้องการตรวจสอบว่าลักษณะของลูกค้าในปีนี้เหมือนปีที่ผ่านมาหรือไม่ จึงสุ่มจากลูกค้า

มา 50 ราย พบว่า เป็นบริษัทเอกชน 20 ราย รัฐบาล 12 ราย ฝ่ายการศึกษา 12 ราย บ้านอยู่อาศัย 4

ราย จงทดสอบที่ระดับนัยสำคัญ .10

3. ผู้สมัครเป็นนายกสโมสรของนิสิตในสถาบันการศึกษาแห่งหนึ่ง มี 5 คน คือหมายเลข 1 – 5 ถ้าผู้สมัครต้องการทราบว่าสัดส่วนของนิสิตที่มีสิทธิ์เลือกตั้งจะเลือกนายกสโมสรแต่ละคนเท่ากันหรือไม่ ก่อนการเลือกตั้งจึงสุ่มนิสิตที่มีสิทธิ์เลือกตั้ง จำนวน 30 คน สอบถามว่าจะเลือกหมายเลขใด ได้ข้อมูล ดังนี้

ผู้สมัครหมายเลข	จำนวนผู้เลือก
1 2 3 4 5	3 9 6 5 7

จงทดสอบที่ระดับนัยสำคัญ .01

4. นักจิตวิทยาเชื่อว่าลูกชายมักจะมีอาชีพเดียวกับพ่อ จึงสุ่มลูกชายมา 60 คน สอบถามอาชีพของเขาและอาชีพของพ่อ ได้ข้อมูล ดังนี้

อาชีพพ่อ	อาชีพลูกชาย
	นักธุรกิจ	ข้าราชการ/วิสาหกิจ	เกษตรกร
นักธุรกิจ ข้าราชการ/วิสาหกิจ เกษตรกร	5 8 6	8 7 5	6 5 10

จงทดสอบความเชื่อของนักจิตวิทยา ที่ระดับนัยสำคัญ .05