EE 635 - Control System Theory

In this class we’ll talk about linear time-invariant systems described by

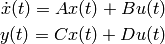
where is a state variable, is an input, and is the output of the system. For a given set of matrices , we will study how to analyse the system behaviour and its important properties. The main goal is to design the input such that the system is stable, i.e.,

More detailed topics covered in this class are given below.

Lecture Notes

Acknowledgement: Most materials will be from the lecture notes of EE263 and EE363, Prof. Stephen Boyd, Stanford University. For each topic in the following, the lectures in () are the corresponding handouts which can be downloaded from EE263 and EE363 websites.

0. Overview (lecture 1, EE263)
1. Linear functions: engineering examples (lecture 2, EE263)
2. Short review on linear algebra and matrix analysis
3. Autonomous linear dynamical systems (lecture 9, EE263)
4. Solution via Laplace transform and matrix exponential (lecture 10, EE263)
5. Eigenvectors and diagonalization (lecture 11, EE263)
6. Jordan canonical form (lecture 12, EE263)
7. Linear dynamical systems with inputs and outputs (lecture 13, EE263)
8. Linear Least-squares and minimum-norm methods (lecture 5 & 8, EE263)
9. Controllability and state transfer (lecture 18, EE263)
10. Observability and state estimation (lecture 19, EE263)
11. Minimal realization and PBH test
12. Observer-Based controller design
13. Basic Lyapunov theory (lecture 12, EE363)
14. Stability of Linear systems and Lyapunov equation
15. LQR and Steady State Riccati equation
16. Estimation (lecture 7, EE363)
17. The Kalman Filter (lecture 8, EE363)
18. Dynamical Control Design with Engineering Applications

Course Information

Lectures:

EE 404, MWF 10-11 am

Textbooks:

• C.T. Chen, Linear System Theory and Design, 2nd edition, 1995
• C.T. Chen, Linear System Theory and Design, 3rd edition, 1998
• T.Kailath, Linear Systems, Prentice-Hall, 1980

Grading:

Weekly Homework 20% Midterm 40% Final 40%

Prerequisites:

Students should have seen topics on linear algebra and matrices. However, a short review will be given briefly in week 1. These topics include vector space, basis/dimension, rank and null space of a matrix, vector/matrix norms, linear equations, eigenvalue problem.