สัญกรณ์เชิงเส้นกำกับ (Asymptotic notation)
ในทางวิทยาการคอมพิวเตอร์ เรามีนิยามที่ใช้ในการวัดความซับซ้อน ที่แทน "in the order of"
ตัวอย่างเช่น t(n) = 27 n2 + 3 n + 12 โดยที่เราอาจคิดว่า n คือขนาดของข้อมูลเข้า และ สูตรของ t ได้
มาจากการนับขั้นตอนการทำงาน จากสูตรนี้เราจะพบว่า เราถือ t(n) is the order of n2 ถ้า f(n) = n2
ใหญ่กว่า t(n) ด้วยผลคูณของค่าคงตัวและทุกค่า n ที่ใหญ่มาก ในทางคณิตศาสตร์ เราเขียนว่า
- t(n) is the order of f(n) ก็ต่อเมื่อ มีจำนวนจริงบวก c และจำนวนนับ n0 ที่ทำให้ t(n)
 c f(n) ทุก n
c f(n) ทุก n  n0 n0
จากตัวอย่างที่ให้ เราเลือก c = 42 และ n0 = 1 แต่เราอาจเลือก c = 28 และ n0 = 6
ดังนั้นถ้าเราเขียนโปรแกรมและใช้เวลาในการคำนวณเป็น 27 n2 + 3 n + 12 วินาที เราเพียงกล่าวว่าเราใช้อันดับ n2
โดยไม่สนใจหน่วย
นิยาม Big-Oh
สำหรับฟังก์ชัน f(n) เรานิยาม O(f(n)) "Big-Oh ของ f(n)" คือ เซตของฟังก์ชันทั้งหมดที่เป็นไปได้
t(n) ซึ่งมี c, n0 ที่ t(n)  c f(n) ทุก
n c f(n) ทุก
n  n0 n0
ตัวอย่างเช่น n2 is O(n3)
โดยทั่วไปในหนังสือ เราจะพบว่าการเขียน O(f(n)) จะเป็นในลักษณะ t(n) = O(f(n)) ซึ่งอาจเป็นการใช้ที่ไม่ถูกต้องนัก
แต่เราก็จะยอมรับการใช้ในลักษณะนี้
กฎ Maximum rule เราสามารถใช้กฎ Maximum rule ในการหาอันดับของฟังก์ชัน โดยที่กฎนี้กล่าวว่า
สำหรับ f(n) และ g(n) ที่เป็นฟังก์ชันบวก O(f(n) + g(n)) = O(max{f(n), g(n)}) หรือ
- ถ้าให้ p(n) = f(n) + g(n) และ q(n) = max{f(n), g(n)}
สำหรับทุกฟังก์ชัน t จะได้ t(n) = O(p(n)) ก็ต่อเมื่อ t(n) = O(q(n))
ตัวอย่างเช่น ถ้าเราวิเคราะห์ขั้นตอนวิธีและพบว่า เราแบ่งการวิเคราะห์ออกเป็นสามส่วนโดยที่แต่ละส่วนมีอันดับคือ
O(n), O(n2) และ O(n log n) จะได้ว่าอันดับของขั้นตอนวิธีนี้คือ O(n + n2 + n log n) โดย
Maximum rule เราจะได้ O(n + n2 + n log n) = O(max{n, n2, n log n}) = O(n2)
จากกฎ Maximum rule ทำให้เราสรุปได้ว่า ถ้า t(n) คำนวณได้จากสูตรที่ซับซ้อนเช่น t(n) = 12 n3 log n
- 5 n2 + log2 n + 36 เราจะสนใจเฉพาะเทอมที่มีการเปลี่ยนแปลงที่มากที่สุดโดยไม่สนใจสัมประสิทธิข้างหน้า
คือ f(n) = n3 log n แล้วเราได้ว่า O(t(n)) = O(f(n)) หรือกล่าวอีกนัยหนึ่งคือ เราสามารถทิ้งเทอมที่มีขนาดเล็กได้จากการพิจารณา
ข้อสังเกตอีกอย่างหนึ่งคือ การพิจารณาฟังก์ชัน log ในเชิงอันดับ เราจะไม่สนใจฐานของ log เพราะเราพบว่า
loga n ต่างกับ logb n เพียงแค่ค่าคงตัวเท่านั้น loga n = loga b *
logb n
สมบัติของ Big-Oh
- Big-Oh มีสมบัติ reflexive นั่นคือ f(n) = O(f(n))
- Big-Oh มีสมบัติ transitive นั่นคือ ถ้า f(n) = O(g(n)) และ g(n) = O(h(n)) แล้ว
f(n) = O(h(n))
กฎที่สำคัญอีกอย่างหนึ่งของ Big-Oh คือ limit rule ซึ่งกำหนดว่า สำหรับฟังก์ชันบวก f และ g ใด ๆ
- ถ้า
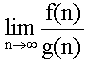 = k แล้ว f(n) = O(g(n)) และ g(n) = O(f(n)) = k แล้ว f(n) = O(g(n)) และ g(n) = O(f(n))
- ถ้า
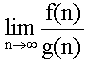 = 0 แล้ว f(n) = O(g(n)) แต่ g(n) ไม่ใช่ Big-Oh ของ f(n) = 0 แล้ว f(n) = O(g(n)) แต่ g(n) ไม่ใช่ Big-Oh ของ f(n)
- ถ้า
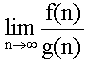 = = 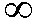 แล้ว f(n) ไม่ใช่ Big-Oh ของ g(n) และ g(n) = O(f(n))
แล้ว f(n) ไม่ใช่ Big-Oh ของ g(n) และ g(n) = O(f(n))
สัญลักษณ์อื่น ๆ ของสัญกรณ์เชิงเส้นกำกับ
เราพบว่าการวิเคราะห์ running time ของ InsertionSort หรือ SelectionSort เราได้ O(n2)
แต่สำหรับ HeapSort หรือ MergeSort เราได้ O(n log n) แต่เนื่องจากว่า n log n = O(n2) เราสามารถกล่าวได้ว่า
HeapSort และ MergeSort คือ O(n2) เราต้องการนิยามขอบเขตล่างในลักษณะคล้ายกับ Big-Oh ซึ่งเราจะเรียกว่า
Big-Omega เขียนแทนด้วย 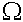
นิยาม Big-Omega
- สำหรับฟังก์ชันบวก f และ t ที่กำหนด เรากล่าวว่า t(n) เป็นอันดับโอเมกาของ f(n),
t(n) = 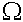 (f(n)) ก็ต่อเมื่อมี d และจำนวนนับ n0 ซึ่ง
t(n) (f(n)) ก็ต่อเมื่อมี d และจำนวนนับ n0 ซึ่ง
t(n)  d f(n) ทุก n d f(n) ทุก n  n0 n0
เราสามารถพิสูจน์ได้โดยง่ายว่า
- t(n) =
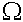 (f(n)) ก็ต่อเมื่อ f(n) = O(t(n)) (f(n)) ก็ต่อเมื่อ f(n) = O(t(n))
เราสามารถพิจารณาว่า 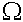 คือขอบเขตล่างในการวิเคราะห์
running time ของขั้นตอนวิธี คือขอบเขตล่างในการวิเคราะห์
running time ของขั้นตอนวิธี
ทั้งนี้ Minimum rule สำหรับ Big-Omega จะคล้ายกับ Maximum rule สำหรับ Big-Oh นั่นคือ สำหรับฟังก์ชันบวก f(n), g(n)
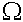 (f(n) + g(n)) = (f(n) + g(n)) =
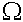 (min{f(n), g(n)}) (min{f(n), g(n)})
นิยาม Theta เขียนแทนด้วย 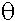
เมื่อเราวิเคราะห์ running time ของขั้นตอนวิธี ถ้าเราพบว่าขั้นตอนวิธีนั้นมีทั้งขอบเขตบนและขอบเขตล่างที่ให้ค่าฟังก์ชัน
เดียวกัน จะทำให้เรามั่นใจว่า ขั้นตอนวิธีจะทำงานภายในระดับที่เราสามารถคาดหวังได้ เรานิยาม Theta ดังนี้
- สำหรับฟังก์ชันบวก f และ t ที่กำหนด เรากล่าวว่า t(n) เป็นอันดับแม่นตรงของ f(n),
t(n) = 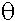 (f(n)) ก็ต่อเมื่อ t(n) = O(f(n)) และ t(n) = (f(n)) ก็ต่อเมื่อ t(n) = O(f(n)) และ t(n) =
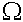 (f(n)) (f(n))
เราได้ Limit rule ซึ่งกำหนดว่า สำหรับฟังก์ชันบวก f และ g ใด ๆ
- ถ้า
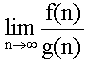 = k แล้ว f(n) = = k แล้ว f(n) = 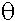 (g(n)) (g(n))
- ถ้า
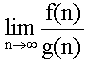 = 0 แล้ว f(n) = O(g(n)) แต่ f(n) ไม่ใช่ theta ของ g(n) = 0 แล้ว f(n) = O(g(n)) แต่ f(n) ไม่ใช่ theta ของ g(n)
- ถ้า
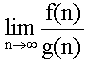 = =  แล้ว
f(n) ไม่ใช่ theta ของ g(n) แต่ f(n) = แล้ว
f(n) ไม่ใช่ theta ของ g(n) แต่ f(n) = 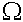 (g(n)) (g(n))
นิยาม little-oh
เราพบว่า Big-Oh ไม่สามารถให้ค่าขอบเขตบนที่ใกล้เคียงกับฟังก์ชันที่ต้องการ เพื่อการกำหนดขอบเขตที่ใกล้เคียง
เราจะใช้ little-oh ควบคู่ โดยที่ little-oh มีนิยามดังนี้
- สำหรับฟังก์ชันบวก f(n) และ t(n), t(n) = o(f(n)) ก็ต่อเมื่อ สำหรับทุก c > 0 มีจำนวนนับ n0 ที่
t(n) < c f(n) ทุก n
 n0 n0
ตัวอย่างเช่น 2 n = o(n2) แต่ 2 n2 ไม่ใช่ o(n2)
เราสามารถกล่าวได้ว่า f(n) เมื่อเทียบกับ g(n) แล้วไม่มีความสำคัญ นั่นคือ 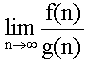 = 0 = 0
นิยาม little-omega
ในทำนองเดียวกับ little-oh เรานิยาม little-omega ได้ดังนี้
- สำหรับฟังก์ชันบวก f(n) และ t(n), t(n) =
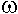 (f(n)) ก็ต่อเมื่อ
สำหรับทุก c > 0 มีจำนวนนับ n0 ที่ t(n) > c f(n) ทุก n (f(n)) ก็ต่อเมื่อ
สำหรับทุก c > 0 มีจำนวนนับ n0 ที่ t(n) > c f(n) ทุก n  n0 n0
ตัวอย่างเช่น n2/2 = 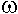 (n) แต่ n2/2 ไม่ใช่ (n) แต่ n2/2 ไม่ใช่
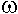 (n2) (n2)
เราสามารถกล่าวได้ว่า f(n) เมื่อเทียบกับ g(n) แล้วใหญ่กว่ามาก นั่นคือ 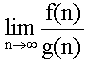 = =
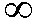
เรายังสามารถแสดงได้ว่า
- f(n) =
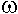 (g(n)) ก็ต่อเมื่อ g(n) = o(f(n)) (g(n)) ก็ต่อเมื่อ g(n) = o(f(n))
การใช้ Conditional asymptotic notation
ในการวิเคราะห์ขั้นตอนวิธีหลายกรณี โดยเฉพาะอย่างยิ่งขั้นตอนวิธีประเภท Divide-and-Conquer
เราพบว่าเรามักแบ่งปัญหาออกเป็นปัญหาย่อย ซึ่งทำให้เราเขียนสมการเวียนเกิดดังตัวอย่างต่อไปนี้
- t(n) = a ถ้า n = 1 และ t(n) = 4 * t([n/2]) + b n ในกรณีอื่น ๆ
ซึ่งการวิเคราะห์โดยพิจารณา [n/2] นั้นยากในการหาคำตอบเพราะค่า n/2 จะไม่เท่ากับ [n/2] ยกเว้นในกรณีที่ n/2 เป็นจำนวนเต็ม
แต่ถ้าเราพิจารณาในกรณีที่ n = 2k เราได้ว่า n/2 จะได้ค่าออกมาเป็นจำนวนเต็มเท่านั้น ดังนั้นการวิเคราะห์หาคำตอบ
จะง่ายขึ้น
- t(n) = (a+b)n2 - b n
นั่นคือเราอาจสนใจเฉพาะ t(n) = O(f(n) | P(n)) ซึ่งหมายความว่า t(n) มีขอบเขตบนจาก f(n) โดยที่ n ต้องมีสมบัติ P(n)
- t(n) = O(f(n) | P(n)) ก็ต่อเมื่อมีจำนวนจริงบวก c และสำหรับ n ที่มีจำนวนไม่จำกัด P(n)
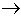 t(n) t(n)  c f(n) c f(n)
สำหรับการใช้ Conditional นี้ เราสามารถจะลดรูปของ P(n) ได้ ถ้า f เป็นฟังก์ชันไม่ลดลงในที่สุด (eventually decreasing) และ
f เป็นฟังก์ชัน b-smooth โดยที่ b  2 2
- เรากล่าวว่า f เป็นฟังก์ชันไม่ลดลงในที่สุด (eventually decreasing) ก็ต่อเมื่อ มีจำนวนเต็มบวก n0 ซึ่งสำหรับ n
 n0, f(n) n0, f(n)  f(n+1) f(n+1)
- สำหรับ b
 2, f เป็นฟังก์ชัน b-smooth ถ้า
f เป็นฟังก์ชันไม่ลดลงในที่สุด (eventually decreasing) และ f(bn) = O(f(n)) 2, f เป็นฟังก์ชัน b-smooth ถ้า
f เป็นฟังก์ชันไม่ลดลงในที่สุด (eventually decreasing) และ f(bn) = O(f(n))
- ฟังก์ชัน f เป็น smooth ฟังก์ชัน ก็ต่อเมื่อ f เป็น b-smooth สำหรับทุก b
 2 2
สัญกรณ์เชิงเส้นกำกับแบบอื่น ๆ
จากนิยามของ Big-Oh, Big-Omega, theta, little-oh, little-omega เราพบว่าเราพิจารณาขนาดของข้อมูลเข้าเพียงหนึ่งตัวแปร
แต่โดยทั่วไป เราอาจพบว่าเรามีจำนวนตัวแปรที่เกี่ยวข้องมากกว่าหนึ่งตัวแปร เช่นขั้นตอนวิธีในการจัดการเรื่องกราฟ G=(V, E)
ซึ่งเรามีจำนวนของจุดยอดและจำนวนของด้านที่ต้องพิจารณา
พิจารณานิยามของ Big-Oh สำหรับสองตัวแปร
- t(m, n) is the order of f(m, n) ก็ต่อเมื่อ มีค่า c และ จำนวนนับ m0, n0 ที่ทำให้ t(m, n)
 c f(m, n) ทุก m c f(m, n) ทุก m  n0 และ
n n0 และ
n  n0 n0
ข้อควรระวังในการพิจารณา Big-Oh ของขั้นตอนวิธีประเภทนี้คือ ค่าของ n0 และ m0 มีความสำคัญที่แตกต่างกัน โดยที่ค่าของ m0
เพียงหนึ่งค่าจะมีค่าของ n จำนวนอนันต์ที่ใช้ร่วมกับ m0 ทำให้กฎต่าง ๆ สำหรับหนึ่งตัวแปรไม่สามารถนำมาใช้ได้โดยตรง
แบบฝึกหัด
- จงพิสูจน์ว่าข้อความต่อไปนี้จริง Transitivity:
- ถ้า f(n) =
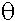 (g(n)) และ
g(n) = (g(n)) และ
g(n) = 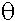 (h(n)) แล้ว
f(n) = (h(n)) แล้ว
f(n) = 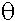 (h(n)) (h(n))
- ถ้า f(n) = O(g(n)) และ g(n) = O(h(n)) แล้ว f(n) = O(h(n))
- ถ้า f(n) =
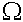 (g(n)) และ
g(n) = (g(n)) และ
g(n) = 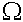 (h(n)) แล้ว
f(n) = (h(n)) แล้ว
f(n) = 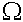 (h(n)) (h(n))
- ถ้า f(n) = o(g(n)) และ g(n) = o(h(n)) แล้ว f(n) = o(h(n))
- ถ้า f(n) =
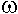 (g(n)) และ
g(n) = (g(n)) และ
g(n) = 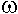 (h(n)) แล้ว
f(n) = (h(n)) แล้ว
f(n) = 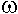 (h(n)) (h(n))
- Reflexivity:
- f(n) =
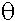 (f(n)) (f(n))
- f(n) = O(f(n))
- f(n) =
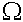 (f(n)) (f(n))
- Symmetry:
- f(n) =
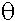 (g(n)) ก็ต่อเมื่อ g(n) = (g(n)) ก็ต่อเมื่อ g(n) =
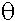 (f(n)) (f(n))
- Transpose symmetry:
- f(n) = O(g(n)) ก็ต่อเมื่อ g(n) =
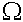 (f(n)) (f(n))
- f(n) = o(g(n)) ก็ต่อเมื่อ g(n) =
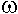 (f(n)) (f(n))
- จงเปรียบเทียบความสัมพันธ์ของ Asymptotic ฟังก์ชันต่อไปนี้
- lg(lg n), 2lg n, n2, n!, (3/2)n, n3, lg2 n,
lg(n!), 22^n, (lg n)!, ln ln n, n*2n, nlg lg n, ln n, 1, 2lg n,
(lg n)lg n, en,. 4lg n, n, 2n, (n+1)!
|