A simple graph and a multigraphs:
A simple graph G = (V, E) consists of a nonempty set of vertices (V) and a set of
unordered pairs of distinct elements of V call edges (E).
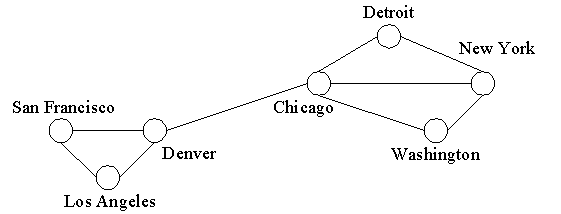
EXAMPLE 1: V = {Detroit, New York, Chicago, Washington, Denver, Los Angeles, San Francisco},
E = {{Detroit, New York}, {Detroit, Chicago}, {Washington, New York}, {Chicago, New York}, {Chicago, Washington},
{Chicago, Denver}, {San Francisco, Denver}, {San Francisco, Los Angeles}, {Los Angeles, Denver} }
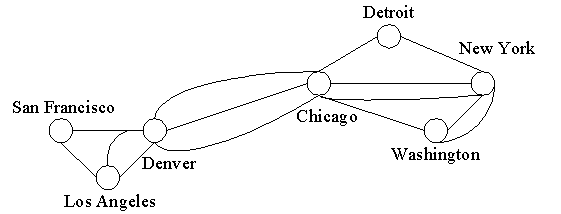
A multigraph G = (V, E) consists of a set of vertices (V), a set of edges (E), and a function
f from E to {{u, v} | u, v  V and u V and u
 v}.
The edges e1 and e2 are called multiple or parallel edges if f(e1) = f(e2). v}.
The edges e1 and e2 are called multiple or parallel edges if f(e1) = f(e2).
A pseudograph G = (V, E) consists of a set V of vertices, a set E of edges, and a function
f from E to {{u, v} | u, v 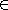 V}. An edge is a loop
if f(e) = {u, u} = {u} for some u V}. An edge is a loop
if f(e) = {u, u} = {u} for some u 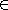 V. V.
A directed graph (V, E) consists of a set of vertices (V) and a set of edges (E), which are ordered pairs
of elements of V.
EXAMPLE 2: V = {Detroit, New York, Chicago, Washington, Denver, Los Angeles, San Francisco},
E = {(New York, Detroit), (Chicago, Detroit), (New York, Washington), (Chicago, New York), (Chicago, Washington),
(Denver, Chicago), (Denver, San Francisco), (San Francisco, Los Angeles), (Los Angeles, Denver) }
A directed multigraph G = (V, E) consists of a set of vertices (V), a set of edges (E), and a
function f from E to {(u, v) | u, v 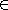 V}.
The edges e1 and e2 are multiple edges if f(e1) = f(e2). V}.
The edges e1 and e2 are multiple edges if f(e1) = f(e2).
| Type | Edges | Multiple edges allowed? | Loops allowed? |
|---|
| Simple graph | Undirected | No | No |
| Multigraph | Undirected | Yes | No |
| Pseudograph | Undirected | Yes | Yes |
| Directed graph | Directed | No | Yes |
| Directed multigraph | Directed | Yes | Yes |
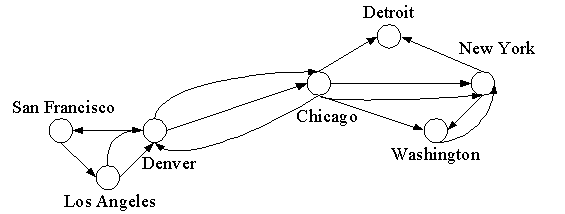
EXAMPLE 3: Niche Overlap Graphs in Ecology:
The competition between species in an ecosystem can be modeled using a niche overlap graph.
Each species is represented by a vertex. An undirected edge connects two vertices if the two species represented by these
vertices compete.
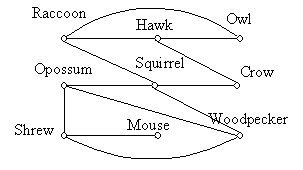
EXAMPLE 4: Influence Graphs:
A directed graph called an influence graph is used to model the behavior of a group of people who can influence the
thinking of others.
Each person of the group is represented by a vertex. There is a directed edge from vertex a to vertex b when the person
represented by vertex a influences the person represented by vertex b.
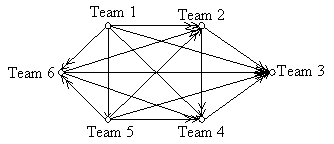
EXAMPLE 5: Round-Robin Tournaments:
A tournament where each team competes each other team exactly once is called a round-robin tournament which is modeled by a directed graphs
where each team is represented by a vertex. Note that (a, b) is an edge if team a beats team b.
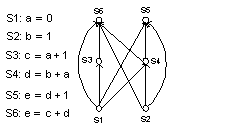
EXAMPLE 6: Precedence graphs and concurrent processing:
Computer programs can be executed more rapidly by executing certain statements concurrently. It is important not to execute a statement that
requires results of statements not yet executed. The dependence of statements on previous statements can be represented by a directed graph.
Each statement is represented by a vertex, and there is an edge from one vertex to a second vertex if the statement represented by the second
vertex cannot be executed before the statement represented by the first vertex. This graph is call a precedence graph.
Definition 1: Two vertices u and v in an undirected graph G are called adjacent
(or neighbors) in G if {u, v} is an edge of G.
The edge e = {u, v} is called incident with the vertices u and v.
The edge e is also said to connect u and v. The vertices u and v are called endpoints of the
edge {u, v}.
Definition 2: The degree of a vertex in an undirected graph is the number of edges incident with it
except that a loop at a vertex contributes twice to the degree of that vertex. We use deg(v) to represent the degree of a vertex v.
EXAMPLE 7:What are the degrees of the vertices of the graph in Example 3?
Theorem 1
Let G = (V, E) be an undirected graph with e edges. Then 2 × e is equal to the sum of deg(v) of
all vertices.
EXAMPLE 8: How many edges are there in a graph with 10 vertices each of degree 6?
Theorem 2 An undirected graph has an even number of vertices of odd degree.
Definition 3: When (u, v) is an edge of the graph G with directed edges, u is said to be
adjacent to v and v is said to be adjacent from u. The vertex u is called the initial vertex of
(u, v) and v is called the terminal (or end) vertex of (u, v).
Definition 4: In a graph with directed edges the in-degree of a vertex v denoted by
deg-(v) is the number of edges with v as their terminal vertex. The out-degree of v, denoted by
deg+(v) is the number of edges with v as their initial vertex.
Theorem 3
Let G = (V, E) be a graph with directed edges. Then the sum of in-degree from all vertices equal to the sum of out-degree from
all vertices which is equal to the total number of edges.
EXAMPLE 9: Complete Graph: The complete graph on n vertices, denoted by Kn, is
the simple graph that contains exactly one edge between each pair of distinct vertices.
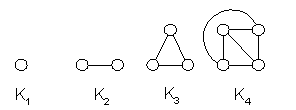
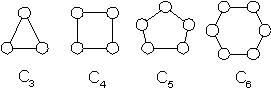
EXAMPLE 10: Cycle: The cycle Cn for n  3,
consists of n vertices: v1, v2, ..., vn and edges {v1, v2},
{v2, v3}, ...,{vn-1, vn}. 3,
consists of n vertices: v1, v2, ..., vn and edges {v1, v2},
{v2, v3}, ...,{vn-1, vn}.
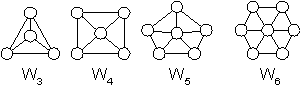
EXAMPLE 11: Wheel: The wheel Wn is obtained from the cycle Cn by adding a new vertex to
the cycle and connect this new vertex to every vertex in the cycle.
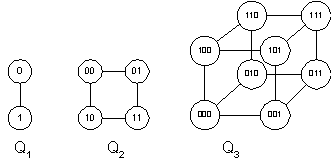
EXAMPLE 12: n-Cubes: The n-Cubes Qn is the graph that has vertices representing the
2n bit strings of length n. Two vertices are adjacent if and only if the bit strings that they represent differ in exactly one bit position.
Definition 5:
A simple graph G is called bipartite if its vertex set V can be partitioned into two disjoint nonempty sets
V1 and V2 such that every edge in the graph connects a vertex in V1 and a vertex in V2.
(No edge in G connects either two vertices in V1 or two vertices in V2).
EXAMPLE 13:C6 is bipartite.
EXAMPLE 14:K3 is not bipartite.
EXAMPLE 15:Are the graph in Example 1 bipartite?
EXAMPLE 16: Complete Bipartite Graph: The complete bipartite graph Km,n is
the graph that has its vertex set partitioned into two subsets of m and n vertices, respectively. There is an edge between two vertices if
and only if one vertex is in the first subset and the other vertex is in the second subset.
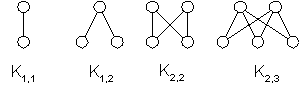
EXAMPLE 17: Local Area Networks The various computers in a building, such as minicomputers and personal computers,
as well as peripheral devices such as printers and plotters, can be connected using a local area network.
Some of these networks are based on a star topology where all devices are connected to a central control devices which can be
represented using a complete bipartite graph, K1, n. Other local area networks are based on a ring topology,
where each device is connected to exactly two others which can be modeled using Cn. Some local area networks use a hybrid of
these two topologies which can be modeled using wheels Wn.
Definition 6 : A subgraph of a graph G = (V, E) is a graph H =
(W, F) where W  V and F V and F  E. E.
EXAMPLE 18: Is the graph Cn a subgraph of Wn?
Definition 7 : The union of two simple graphs, G1 = (V1, E1)
and G2 = (V2, E2) is the simple graph with vertex set V1
 V2 and edge set E1 V2 and edge set E1
 E2. The union of G1 and G2 is denoted by G1 E2. The union of G1 and G2 is denoted by G1
 G2. G2.
Definition 8 : A path of length n, where n is a positive integer, from u to
v in a directed multigraph is a sequence of edges e1, ..., en of the graph such that f(e1) =
(x0, x1), f(e2) = (x1, x2), ..., f(en) = (xn-1,
xn), where x0 = u and xn = v. When there are no multiple edges in the graph, this path is denoted
by its vertex sequence, x0, x1, ... , xn. A path that begins and ends at the same vertex is called a circuit
or cycle. A path or circuit is called simple if it does not contain the same edge more than once.
Definition 9 : An undirected graph is called connected if there is a path between every pair of
distinct vertices of the graph.
Theorem 4 : There is a simple path between every pair of distinct vertices of a connected undirected graph.
Definition 10 : A directed graph is strongly connected if there is a path from a to b
and from b to a whenever a and b are vertices in the graph.
Definition 11 : A directed graph is weakly connected if there is a path between any two vertices
in the underlying undirected graph.
Implementation of Graphs:
There are two standard ways to represent a simple graph. One is called adjacency lists and the other method is called
adjacency matrices.
Adjacency Lists
Let nodes be named by the integers 0, 1, ..., MAX-1. We can then use the characteristic-vector to represent the set of arcs or edges.
We define linked lists of nodes by
- typedef struct CELL *LIST
- struct CELL {
- NODE nodeName;
- LIST next;
- };
and then create an array
- LIST successors[MAX];
That is, the entry successors[u] contains a pointer to a linked list of all the successors of node u.
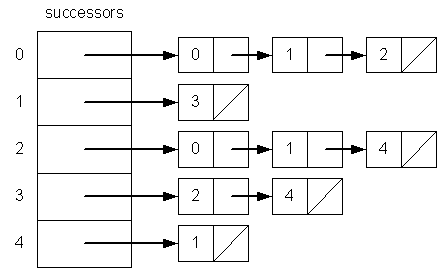
EXAMPLE 19: Draw the graph of the corresponding adjacency list above.
Adjacency Matrices
Another common way to represent directed graphs is adjacency matrices. We use a two-dimensional array as
- BOOLEAN arcs[MAX][MAX];
The value of arcs[u][v] is TRUE if there is an arc (u, v) in the graph and FALSE otherwise.
EXAMPLE 20: Write the adjacency matrix from Example 19 above.
Definition 12 : Let G = (V, E) is a simple graph where | V | = n. Suppose that the vertices of G are
listed arbitrarily as v1, v2, ..., vn. The adjacency matrix A of G, with respect to this listing of the
vertices, is the n × n zero-one matrix with 1 as its (i, j)th entry when vi and vj are adjacent,
and 0 as its (i,j)th entry when they are not adjacent.
Theorem 5 : Let G be a graph with adjacency matrix A with respect to the ordering v1,
v2, ..., vn (with directed or undirected edges, with multiple edges and loops allowed). The number of different paths of length
r from vi to vj, where r is a positive integer, equals the (i, j)th entry of Ar.
|