Graph searching:
For graph searching, we view a graph G = (V, E) with a vertex as a state and an edge as an operator. The graph searching
algorithm then start from the initial state applying the appropriate operators to change to the new states until it reaches a state in the set of possible
goal states. We may also call this the state-space search which is defined as (s, O, G) where
- s is the initial state
- O is the set of available operators
- G is the set of goal states
The solution of the graph searching algorithm is the path from the initial state to the goal state via a specific order of the operators. In the case of
searching without any knowledge or objective, we called the method, blind search. Two of the most popular blind search methods are
breadth-first search and depth-first search.
Breadth-first search
The main step of the breadth-first search algorithm considers all reachable states level by level where the level is the length from the initial state to the
current state. This method guarantees that the solution is the path with the shortest level.
Breadth-first search(G, s, Q)
INPUT: G is a graph, s is the initial state and Q is the set of goal states.
OUTPUT: A path from the initial state to the goal state.
1. Put the initial state on a list, called OPEN, of unexpanded states.
2. If the initial state is a goal state then
3. return "a solution has been found."
4. endif
5. If OPEN is empty then
6. return "no solution exists."
7. endif
8. Remove the first state, n, from OPEN and place it in a list, called CLOSED, of expanded states.
9. Expand state n.
10. If it has no successors then
11. go to 5
12. endif
13. Place all successors of state n at the end of the OPEN list.
14. If any of the successors of state n is a goal state then
15. return "a solution has been found."
16. else
17. go to 5
18. endif
Depth-first search
The depth-first search considers the current state from the latest generated state. The search will continue until the current state can not expand and
it is not one of the goal state. Then the algorithm will backtrack to the previous state and search again to the different state.
Depth-first search(G, s, Q)
INPUT: G is a graph, s is the initial state and Q is the set of goal states.
OUTPUT: A path from the initial state to the goal state.
1. Put the initial state on a list, called OPEN, of unexpanded states.
2. If the initial state is a goal state then
3. return "a solution has been found."
4. endif
5. If OPEN is empty then
6. return "no solution exists."
7. endif
8. Move the first state, n, on OPEN to a CLOSED list, of expanded nodes.
9. If the depth of state n is equal to the maximum depth then
10. go to 5.
11. endif
12. Expand node n.
13. If it has no successors then
14. go to 5.
15. endif
16. Place all successors of state n at the beginning of OPEN.
17. If any of the successors of node n is a goal node then
18. return "a solution has been found"
19. else
20. go to 5.
21. endif
Euler and Hamilton Paths:
The town of Königsberg, Prussia was divided into four sections by the branches of the Pregel River.
In the eighteenth century seven bridges connected these regions together as in the figure below.
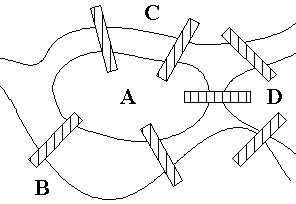 The towns people took long walks through town on Sundays. They wondered whether it was possible to start at
some location in the town, travel across all the bridges without crossing any bridge twice, and return to the starting point.
The towns people took long walks through town on Sundays. They wondered whether it was possible to start at
some location in the town, travel across all the bridges without crossing any bridge twice, and return to the starting point.
The problem can be rephrased as: Is there a simple circuit in this multigraph that contains every edge?
Definition 1: An Euler circuit in a graph G is a simple circuit containing every edge of G.
An Euler path in G is a simple path containing every edge of G.
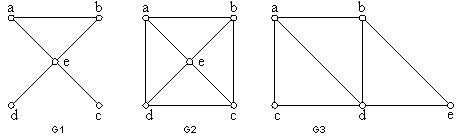
EXAMPLE 1: Which of the undirected graphs have an Euler circuit? Of those that do not, which have an Euler path?
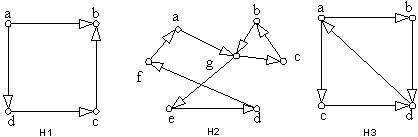
EXAMPLE 2: Which of the directed graphs have an Euler circuit? Of those that do not, which have an Euler path?
Theorem 1: A connected multigraph has an Euler circuit if and only if each of its vertices has even degree.
To prove this, we must show that every Euler circuit has even degree vertices and then show that for any graph
with an even degree of vertices, we can construct the Euler circuit.
- Given an Euler circuit begins with a vertex a, using the edge {a, b}.
- We have that edge {a,b} contribute 1 to deg(a).
- Every time the circuit passes through a vertex it contributes 2 to the degree of the vertex (one in and one out.)
- Since the circuit terminates where it starts, it contributes additional 1 to deg(a).
- Therefore, the deg(a) must be even.
- Since the circuit passes through every edge and contribute only even number of degree to all vertices in the path.
Therefore, every vertex must have even degree.
- If we have even degree for all vertices, then we can construct the Euler circuit as followed:
- Start at an arbitrary vertex a.
- Choose an edge {a, x1} incident with a.
- Remove it from the graph.
- We continue by building a simple path {a, x1}, {x1, x2}, ..., {xn, a}.
- We must stop at a because each edge has even degree.
- When we enter one edge (reducing one from the degree of that vertex), then there will be at least one edge out.
- Only way it stops when it comes back to a and has no edge out. If we have all edges then we are done.
- Otherwise, we have a subgraph H obtained from G by deleting the edges that have been used.
- This H must have a vertex common with the simple path that we have before called w, because G is connected.
- By applying the procedure with H using the vertex w, we can construct a simple circuit that starts with w and end with w.
- Merge this to our previous circuit, we will have a simple circuit with more edges.
- We continue this process until all edges have been used. This is possible because we have a finitely many edges.
- The last simple circuit is the Euler circuit.
ALGORITHM 1: Constructing Euler Circuits.
INPUT: G is a connected multigraph with all vertices of even degree.
OUTPUT: C is an Euler circuit.
1. C = ({a, x1}, {x1, x2}, ..., {xn, a})
2. H = G with the edge from C removed
3. while H has edges
4. Pick one vertex from C that has edge in H
5. Create subcircuit with that vertex
6. H = H with the edge from subcircuit removed
7. C = circuit with the subcircuit inserted at that selected vertex
8. endwhile
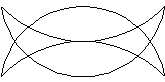
EXAMPLE 3:Is it possible to identify which pictures can be drawn in a continuous motion without lifting a pencil
so that no part of the picture is retraced? The idea is to use the Euler circuit. For example, the Mohammed's scimitars can be drawn this way.
Theorem 2 : A connected multigraph has an Euler path but not an Euler circuit if and only if it has exactly
two vertices of odd degrees.
EXAMPLE 4: Which graphs have an Euler path?

Definition 2 A path x0, x1, ..., xn-1 in the graph G = (V, E) is called
a Hamilton path if V = {x0, x1, ..., xn} and xi
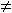 xj for 0 xj for 0 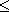 i i
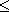 j j 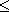 n. A circuit x0, x1,
..., xn-1, xn, x0 (with n > 1) in a graph G = (V, E) is called a Hamilton circuit if x0,
x1, ..., xn-1, xn is a Hamilton path. n. A circuit x0, x1,
..., xn-1, xn, x0 (with n > 1) in a graph G = (V, E) is called a Hamilton circuit if x0,
x1, ..., xn-1, xn is a Hamilton path.
EXAMPLE 5: Which graphs have a Hamilton circuit or Hamilton path (if not)?
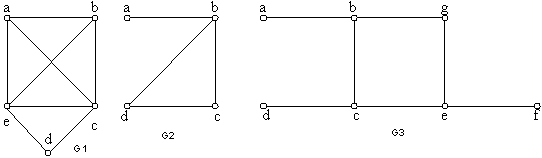
EXAMPLE 6: Show that neither graph has a Hamilton circuit.
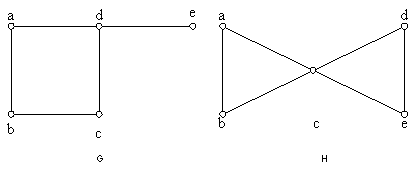
EXAMPLE 7: Show that Kn has a Hamilton circuit whenever n 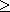 3. 3.
Theorem 3: If G is a connected simple graph with n vertices where n
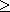 3, then G has a Hamilton circuit if the degree of each vertex is at least n/2. 3, then G has a Hamilton circuit if the degree of each vertex is at least n/2.
EXAMPLE 8: Gray CodesThe position of a rotating pointer can be represented in digital form. One way to do this is to
split the circle into 2n arcs of equal length and to assign a bit string of length n to each arc.
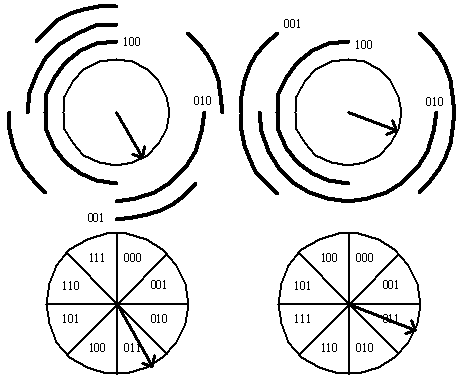
The digital representation of the position of the pointer can be determined using a set of n contacts.
To minimize the effect of an error in determining the position of the pointer, the assignment of the bit strings to the 2n arcs should be
made so that only one bit is different in the bit strings represented by adjacent arcs.
The Gray code is a labeling of the arcs of the circle so that adjacent arcs are labeled with bit strings that differ in exactly one bit.
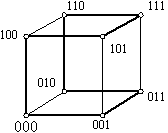
We can model this problem using the n-cube, Qn
Graphs that have a number assigned to each edge are called weighted graphs.
Weighted graphs are used to model computer networks with communication costs, the response times of the computer over the line,
or the distance between computers.
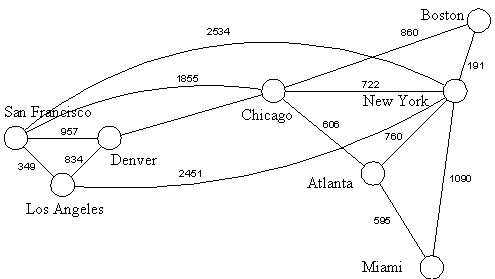
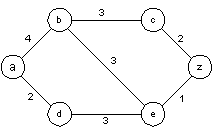
EXAMPLE 1: What is the length of the shortest path between a and z in the weighted graph?
ALGORITHM: Dijkstra's A connected multigraph has an Euler circuit if and only if each of its vertices has
even degree.
Dijkstra(G, a, z)
INPUT G is an adjacency list, a is the source vertex and z is the destination vertex.
OUTPUT L is a vector of the shortest path from a to that current vertex.
1. for vi in V[G]
2. L(vi) = infinity
3. endfor
4. L(a) = 0
5. S = Ø
6. while( z is not in S)
7. u = a vertex not in S with minimal L(u)
8. S = S  {u}
9. for each v not in S
10. if L(u) + w(u, v) < L(v) then
11. L(v) = L(u) + w(u,v)
12. endif
13. endfor
14. endwhile {u}
9. for each v not in S
10. if L(u) + w(u, v) < L(v) then
11. L(v) = L(u) + w(u,v)
12. endif
13. endfor
14. endwhile
EXAMPLE 2:Use Dijkstra's algorithm to find the length of the shortest path between the vertices a and z in the weighted graph.
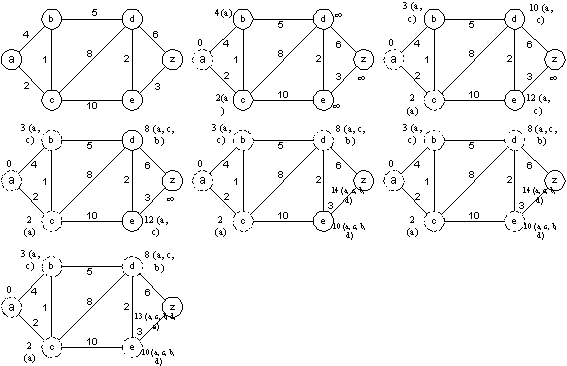
We use an inductive argument to show that Dijkstra's algorithm produces the length of the shortest path between two vertices.
At the kth iteration
- the label of a vertex v, v
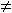 0, in S is the length of the shortest path from a to this vertex,
and 0, in S is the length of the shortest path from a to this vertex,
and
- the label of a vertex not in S is the length of the shortest path from a to this vertex that contains only vertices in S.
Theorem 1 : Dijkstra's algorithm finds the length of a shortest path between two vertices in a connected simple
undirected weighted graph.
Theorem 2 : Dijkstra's algorithm uses O(n2) operations to find the length of the shortest path
between two vertices in a connected simple undirected weighted graph.
The traveling salesman problem
A traveling salesman wants to visit each of n cities exactly once and return to his starting point. In which order should he visit
these cities to travel the minimum total distance?
The problem is just the searching for the circuit of minimum total weight in a complete undirected graph that visits each vertex exactly once
and returns to its starting point. This is equivalent to finding a Hamilton circuit with minimum total weight in the complete graph.
The most straightforward way to solve an instance of the traveling salesman problem is to examine all possible Hamilton circuits and select
one of minimum total length.
How many circuits do we have to examine to solve the problem if there are n vertices in the graph?
Planar graph
Consider the problem of joining three houses to each of three separate utilities. Is it possible to join these houses and
utilities so that none of the connections cross?
This problem can be modeled using the complete bipartite graph K3,3. Can K3,3 be drawn in the plane so that
no two of its edges cross?
Definition 1: A graph is called planar if it can be drawn in the plane without any edges crossing (where a crossing of edges
is the intersection of the lines or arcs representing them at a point other than their common endpoint). Such a drawing is called a
planar representation of the graph.
EXAMPLE 1: Is K4 planar?
EXAMPLE 2: Is Q3 planar?
EXAMPLE 3: Is K3, 3 planar?
Theorem 3: Euler's formula Let G be a connected planar simple graph with e edges and v vertices.
Let r be the number of regions in a planar representation of G. Then r = e - v + 2.
EXAMPLE 4: Suppose that a connected planar simple graph has 20 vertices, each of degree 3. Into how many regions does a
representation of this planar graph split the plane?
Corollary 1: If G is a connected planar simple graph with e edges and v vertices where v
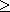 3, then e 3, then e 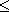 3 v - 6. 3 v - 6.
EXAMPLE 5: Show that K5 is nonplanar using Corollary 1?
Corollary 2: If a connected planar simple graph has e edges and v vertices with v
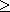 3 and no circuits of length 3, then e 3 and no circuits of length 3, then e 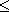 2 v - 4. 2 v - 4.
EXAMPLE 6: Use Corollary 2 to show that K3,3 is not planar.
Kuratowski's theorem: Given a planar graph, G = (V, E). If we remove an edge {u, v} in E and adding a new
vertex w to V and new edges {u, w}, {w, v} in E, we will have a new planar graph G'. We call this operation an elementary subdivision
operation. The graph G1 and G2 are homeomorphic if they can be obtained from the same graph by a sequence of elementary subdivisions.
Theorem 4: A graph is nonplanar if and only if it contains a subgraph homeomorphic to K3, 3
or K5.
EXAMPLE 7: Determine whether the graph G shown is planar?
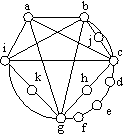
EXAMPLE 8: Is the Petersen graph planar?
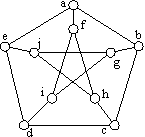
|