นักวิทยาศาสตร์ ต้องสำนึกใน 5 W
What อะไร
Where ที่ไหน
When เมื่อไหร่
Why ทำไม
Who ใครเกี่ยวข้อง
ทบทวนลิมิต
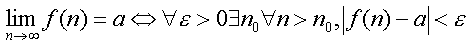
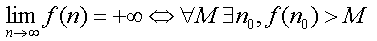
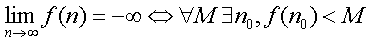
- f(n) แกว่งเมื่อ n
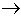 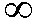 iff มีจำนวนจริง K ซึ่งสำหรับทุก ๆ n ที่เป็นจำนวนนับ -K < f(n) < K เช่น (-1)n
iff มีจำนวนจริง K ซึ่งสำหรับทุก ๆ n ที่เป็นจำนวนนับ -K < f(n) < K เช่น (-1)n
ถ้า 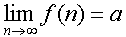 และ และ 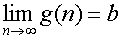 แล้ว แล้ว
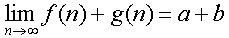
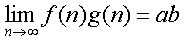
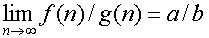 เมื่อ b ไม่ใช่ 0 เมื่อ b ไม่ใช่ 0
- ถ้า f(n)
 g(n) สำหรับ n ที่ใหญ่ขึ้นไปแล้ว a g(n) สำหรับ n ที่ใหญ่ขึ้นไปแล้ว a
 b b
- ถ้า
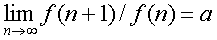 เมื่อ -1 < a < 1 แล้ว เมื่อ -1 < a < 1 แล้ว 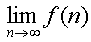 = 0
แต่ถ้า f(n) เป็นบวก และ a > 1 แล้ว = 0
แต่ถ้า f(n) เป็นบวก และ a > 1 แล้ว 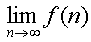 = +
= +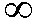
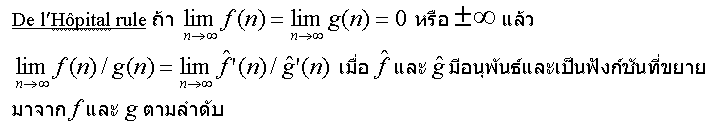
ตัวอย่าง จงหาค่าลิมิตต่อไปนี้
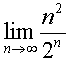 , , 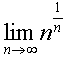 , ,
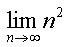 , , 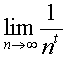 เมื่อ t > 0, เมื่อ t > 0,
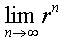 เมื่อ | r | < 1, เมื่อ | r | < 1, 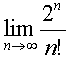
ทบทวน เรื่องอนุกรม
กำหนดลำดับ {an}, นิยามอนุกรม Sn ดังนี้
Sn = 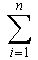 an an
ถ้า 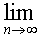 Sn = S แล้ว Sn ลู่เข้า Sn = S แล้ว Sn ลู่เข้า
อนุกรมเลขคณิต a, a+d, a+2d, ..., a+(n-1)d
อนุกรมเรขาคณิต a, ar, ar2, ..., arn-1
- สำหรับอนุกรมเลขคณิต Sn =
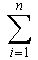 a + (i-1)d a + (i-1)d
จะได้ Sn = a n + n (n - 1) d/2
- สำหรับอนุกรมเรขาคณิต Sn =
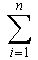 a ri - 1 a ri - 1
จะได้ Sn = a (1 - rn)/(1 - r) กรณี r ไม่เท่ากับ 1 และ Sn = a n กรณี r = 1
- อนุกรมเรขาคณิตแบบอนันต์
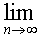 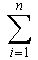 a ri-1 ลู่เข้า a ri-1 ลู่เข้า
ก็ต่อเมื่อ -1 < r < 1 และค่าที่ลู่เข้าคือ a/(1-r)
- r + 2 r2 + 3 r3 + ... ลู่เข้าเมื่อ -1 < r < 1 และลู่เข้า r/(1-r)2
-
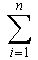 1 = n 1 = n
-
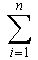 i(i+1)...(i+k) = n(n+1)...(n+k+1)/(k+2) เราจะได้ว่า i(i+1)...(i+k) = n(n+1)...(n+k+1)/(k+2) เราจะได้ว่า
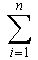 i = n(n+1)/2 และ i = n(n+1)/2 และ
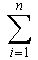 i2 = n(n+1)(2n+1)/6 i2 = n(n+1)(2n+1)/6
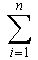 rr = nr+1/(r+1) + pr(n) เมื่อ r > 0 และ rr = nr+1/(r+1) + pr(n) เมื่อ r > 0 และ
pr(n) เป็นโพลิโนเมียลฟังก์ชันดีกรีอย่างมาก r
พิจารณาลำดับ 1-r, 2-r, ... เมื่อ r > 0
สำหรับกรณี r = 1, จะได้ 1, 1/2, 1/3, ... เรียกลำดับฮาร์มอนิก
- ถ้า Hn เป็นผลบวก n พจน์แรกของลำดับฮาร์มอนิกแล้ว
log(n+1) < Hn < 1 + log n
ตัวอย่าง จงหาค่าของอนุกรมต่อไปนี้
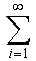 1/(n+1)(n+2), 1/(n+1)(n+2),
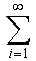 1/2n, 1/2n, 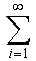 (n/(n+1))n (n/(n+1))n
นิยามวิธีเรียงสับเปลี่ยน (Permutation)
วิธีเรียงสับเปลี่ยนของสิ่งของ n สิ่งคือ การจัดเรียงสิ่งของ n สิ่งที่แตกต่างกันทั้งหมด
ตัวอย่างเช่น เรามีของ 4 ชนิด: ก ข ค ง
เราสามารถจัดเรียงได้ 24 แบบที่แตกต่างกัน
กขคง กขงค กคขง กคงข กงขค กงคข
ขกคง ขกงค ขคกง ขคงก ขงกค ขงคก
คกขง คกงข คขกง คขงก คงกข คงขก
งกขค งกคข งขกค งขคก งคกข งคขก
จำนวนวิธีเรียงสับเปลี่ยนทั้งหมดเท่ากับ
n (n - 1) (n - 2) ... 2 1 = n!
นิยามวิธีจัดหมู่ (Combination)
วิธีจัดหมู่ของสิ่งของ r สิ่งจากของทั้งหมด n สิ่ง คือการเลือกสิ่งของออกมา r สิ่ง
โดยไม่สนใจอันดับที่ถูกเลือกขึ้นมา
ตัวอย่างเช่น เรามีของ 5 ชนิดต้องการเลือกออกมา 3 ชนิด: ก ข ค ง จ
เราสามารถจัดหมู่ได้ 10 แบบคือ
กขค กขง กขจ กคง กคจ กงจ
ขคง ขคจ ขงจ คงจ
จำนวนวิธีเลือกของ r สิ่งจาก n โดยที่ลำดับมีความสำคัญเท่ากับ
n (n - 1) (n - 2) ... (n - r + 1)
ซึ่งเราจะถือว่าสิ่งของ r สิ่งนั้นจะไม่แตกต่างกัน
ดังนั้นจะได้ 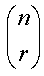 = n (n - 1) (n - 2) ... (n - r + 1)/r!
= n (n - 1) (n - 2) ... (n - r + 1)/r!
นอกจากนี้ 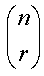 ยังถูกเรียกว่าเป็น binomial coefficient ยังถูกเรียกว่าเป็น binomial coefficient
| n\r | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | | | | | |
| 1 | 1 | 1 | | | | |
| 2 | 1 | 2 | 1 | | | |
| 3 | 1 | 3 | 3 | 1 | | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 1 | 5 | 10 | 10 | 5 | 1 |
ทบ. (Newton) การจัดหมู่
(1+x)n = 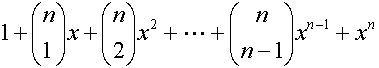
ถ้ากำหนดค่า x = 1 เราจะได้ 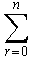
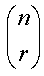 = 2n = 2n
ถ้ากำหนดค่า x = -1 เราจะได้ 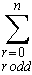
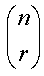 = = 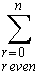
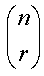
บททบทวน ความน่าจะเป็น
- Experiment
- Random experiment
- outcome
- Sample space
- Sample point (Elementary event)
- Universal event
- Impossible event
- Probability measure
- Conditional probability of A given B
- Random variable
- Probability mass function of X
- Expectation of X
- Variance of X
- Standard deviation of X
นิยามการวัดความน่าจะเป็น (Probability measure)
กำหนดให้ S เป็นเซตของ Sample Space
- สำหรับเหตุการณ์ A ใด ๆ, Pr[A]
 0 0
- Pr[S] = 1
- ถ้า A และ B เป็นเหตุการณ์ที่ไม่มีสมาชิกร่วมกัน
นั่นคือ A  B = Ø
แล้ว Pr[A B = Ø
แล้ว Pr[A 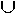 B] = Pr[A] + P[B] B] = Pr[A] + P[B]
ถ้า Ai  Aj = Ø แล้ว
Pr[A1 Aj = Ø แล้ว
Pr[A1 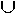 A2
A2 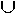 . . .
An] = Pr[A1] + Pr[A2] + . . . + Pr[An] . . .
An] = Pr[A1] + Pr[A2] + . . . + Pr[An]
เราจะได้
- Pr[AC] = 1 - Pr[A]
- Pr[A
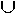 B] = Pr[A] + P[B] -
Pr[A B] = Pr[A] + P[B] -
Pr[A  B] B]
ตัวอย่าง ความน่าจะเป็น
- S = {1, 2, 3, 4, 5, 6} และแต่ละ Elementary event มีความน่าจะเป็นในการเกิดเท่ากัน
ถ้า A = {ตัวเลขที่ปรากฎเป็นเลขคี่} จะได้ Pr[A] =
ถ้า B = {ตัวเลขที่ปรากฎน้อยกว่า 2} จะได้ Pr[B] =
- S = {0, 1, 2, ..., 9999} และแต่ละ Elementary event มีความน่าจะเป็นในการเกิดเท่ากัน
ถ้า A = {จำนวนเฉพาะใน S} จะได้ Pr[A] =
ถ้า A = {จำนวนเฉพาะใน S} แต่เราทราบว่ามีเหตุการณ์ B={จำนวนคี่} ที่เกิดก่อน จะได้ Pr[A | B] =
นิยามความน่าจะเป็นมีเงื่อนไข (Conditional probability)
สำหรับเหตุการณ์ A และ B ใด ๆ ที่ Pr[B] 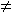 0,
Pr[A | B ] = Pr[ A 0,
Pr[A | B ] = Pr[ A  B] / Pr[B] B] / Pr[B]
นิยามความเป็นอิสระต่อกัน (Independent)
สำหรับเหตุการณ์ A และ B ใด ๆ, ถ้า A เป็นอิสระกับ B แล้ว
Pr[ A  B] = Pr[A] Pr[B] B] = Pr[A] Pr[B]
ในกรณีที่ Pr[B] 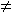 0, แล้ว
Pr[A | B] = Pr[A 0, แล้ว
Pr[A | B] = Pr[A  B] / Pr[B] = Pr[A] B] / Pr[B] = Pr[A]
นิยามตัวแปรสุ่ม (Random variable)
ตัวแปรสุ่มเป็นฟังก์ชันซึ่งกำหนดค่าสำหรับแต่ละจุด (sample point) ใน sample space S
ตัวอย่างเช่น จำนวนครั้งที่ชนะในการแข่งม้า หรือจำนวนครั้งที่ลูกเต๋าออกเลขคี่
เรานิยาม p(x) = Pr[X = x] เมื่อ x แทนค่าที่อาจเป็นไปได้ของตัวแปรสุ่ม เรียก p(x) ว่า
probability mass function of X
นิยามค่าคาดหมายของตัวแปรสุ่ม X (Expectation)
E[X] = 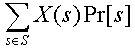 = =
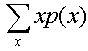
ตัวอย่าง
พิจารณาการแข่งม้าซึ่งมีม้า 5 ตัว คือ Ariel, Bonbon, Coffee, Demon, Eggcup
โดยที่ผลลัพธ์ที่เราสนใจคือ ม้าที่แข่งชนะ
เราจะได้ S = {Ariel, Bonbon, Coffee, Demon, Eggcup}
สมมติเราทราบจากสถิติการแข่งก่อนหน้านี้และกำหนด probability measure ไว้ดังนี้
| Outcome |
Probability |
Winnings |
| Ariel |
0.10 |
50 |
| Bonbon |
0.05 |
100 |
| Coffee |
0.25 |
-30 |
| Demon |
0.50 |
-30 |
| Eggcup |
0.10 |
15 |
ในสดมภ์ Winnings เรากำหนดค่าซึ่งจะบอกว่าเราจะได้หรือเสียเท่าไหร่ เรียก ตัวแปรสุ่ม W
เราสามารถคำนวณ p(x) ได้ดังนี้
p(-30) = Pr[W = -30] = Pr[Coffee] + Pr[Demon] = 0.25 + 0.50 = 0.75
p(15) = Pr[W = 15] = 0.10, p(50) = Pr[W = 50] = 0.10 และ
p(100) = Pr[W = 100] = 0.05
ค่าคาดหวังของ W, E[W] = 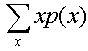 =
-30 p(-30) + 15 p(15) + 50 p(50) + 100 p(100) = -11 =
-30 p(-30) + 15 p(15) + 50 p(50) + 100 p(100) = -11
เรากำหนด ความแปรปรวน (Variance) ของตัวแปรสุ่ม X คือ
Var[X] = E[(X - E[X])2] = 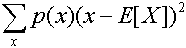
และค่าเบี่ยงเบนมาตรฐานคือ รากที่สองของ Var[X]
|