การพิสูจน์โดยอุปนัยเชิงคณิตศาสตร์
อุปนัยเชิงคณิตศาสตร์ (Mathematical Induction) คือการพิสูจน์สำหรับประโยคที่มีตัวแปรเป็นจำนวนนับ
โดยการพิสูจน์อาศัยหลักที่ว่า ประโยคเริ่มต้นเป็นจริง (คือ P(1) เป็นจริง) และถ้าเราสามารถแสดงว่า การพิสูจน์ค่าความจริงของประโยค P(n+1)
เกิดจากค่าความจริงของประโยค P(n) เราจะได้ว่า P(n) เป็นจริงทุกค่าของ n
พิจารณาปัญหาต่อไปนี้
- 1. สูตรทั่วไปของการบวกตัวเลขจาก 1 ถึง n มีหรือไม่ ถ้ามีคืออะไร พิสูจน์อย่างไร
- 2. สูตรทั่วไปของการบวกตัวเลขคี่จาก 1 ถึง n มีหรือไม่ ถ้ามีคืออะไร พิสูจน์อย่างไร
- 3. สูตรทั่วไปของการบวกตัวเลขคู่จาก 1 ถึง n มีหรือไม่ ถ้ามีคืออะไร พิสูจน์อย่างไร
อุปนัยเชิงคณิตศาสตร์ : ให้ S 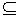
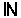 , ถ้า S มีสมบัติว่า , ถ้า S มีสมบัติว่า
1. 1 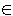 S S
2. สำหรับจำนวนเต็มบวก k ถ้า k 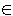 S แล้ว k+1 S แล้ว k+1
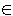 S S
จะได้ว่า S = 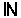
เราเรียก ประโยคในข้อ 1. ว่า มูลฐานของการอุปนัย (basis of induction) และ ประโยคข้อ 2. ว่า ขั้นอุปนัย (inductive step)
และเรียกสมมติฐานในประโยคข้อ 2. ที่ว่า k 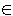 S ว่า สมมติฐานของการอุปนัย
(inductive hypothesis) S ว่า สมมติฐานของการอุปนัย
(inductive hypothesis)
ตัวอย่าง จงพิสูจน์ว่า
- 12 + 22 + 32 + . . . + n2 = n(2n+1)(n+1)/6
- 1 + 3 + 5 + 7 + . . . + (2 n - 1) = n2
- n < 2n
- n3 - n หารด้วย 3 ลงตัว
- 1 + 2 + 22 + . . . + 2n = 2n+1 - 1
- 1 + 2 + 3 + . . . + n = n (n + 1)/2
- 2n < n! สำหรับทุก n > 3
อุปนัยเชิงคณิตศาสตร์แบบเข้ม
ให้ S 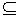 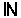 , ถ้า S มีสมบัติว่า , ถ้า S มีสมบัติว่า
1. 1 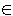 S S
2. สำหรับจำนวนเต็มบวก k ถ้า 1, 2, 3, ..., k 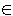 S แล้ว
k+1 S แล้ว
k+1 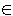 S S
จะได้ว่า S = 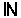
ตัวอย่าง จงพิสูจน์ว่า
an < (7/4)n เมื่อกำหนดให้ a1 = 1, a2 = 3 และ
an = an-1 + an-2 สำหรับ n > 2
|
|