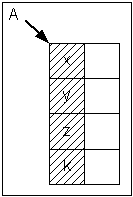
• Array
• Stack
• Queue
• Linked list
• Tree
• Heap
• Hashing array

นิยามข้อมูลแบบแถวลำดับ (Array)
ข้อมูลแบบแถวลำดับมีคุณลักษณะคือ

1. มีจำนวนที่สำหรับเก็บข้อมูลจำกัด ต้องทราบจำนวนข้อมูลก่อนเริ่มใช้ (ปัจจุบันมีการใช้ Dynamic array ซึ่งพยายามลดข้อจำกัดในส่วนนี้)
2. ข้อมูลแต่ละตัวมักจะเป็นประเภทเดียวกัน และมีขนาดเท่ากัน
3. มีการเข้าถึงข้อมูลโดยใช้ ดรรชนี (index) ซึ่งเป็นตัวเลข

การกระทำบนข้อมูลแถวลำดับประกอบด้วย

1. insert an element
2. search for an element in the list
3. retrieve the element
4. delete the element
5. check if the array is empty
6. check if the array is full
7. find the number of elements

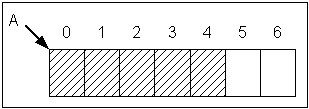
เราเขียนโครงสร้างข้อมูลแถวลำดับสำหรับจำนวนจริงได้ดังนี้

int MAXARRAY=100;

double A[MAXARRAY];

int nA=0;

1. การเติมข้อมูล เพื่อความรวดเร็วเราจะเติมข้อมูล ณ ตำแหน่งท้ายสุด
   1. insert(A, e)

      if(not full(A)) then A[nA++] = e

2. การค้นหาข้อมูล
   เราแบ่งการค้นหาออกเป็นสามแบบ คือ การค้นหาสมาชิก e, การค้นหาค่าสูงสุดและการค้นหาค่าต่ำสุด
   1. search(A, e)

      for(i = 0; i < nA; i++) {

      if(A[i] == e) then return i;

      return "not found"

   2. search_max(A)

      j = 0; max = A[j];

      if(nA <= 0) then return "no"

      for(i = 1; i < nA; i++) {

      if(A[i] > max) then

          j = i; max = A[j];

      return max, j;

   3. search_min(A)

      j = 0; min = A[j];

      if(nA <= 0) then return "no"

      for(i = 1; i < nA; i++) {

      if(A[i] < min) then

          j = i; min = A[j];

      return min, j;

3. การเรียกข้อมูล
   เราแบ่งเป็นสี่แบบคือ ทราบตำแหน่ง i, ทราบค่า e, ค่าที่สูงที่สุด และค่าที่ต่ำที่สุด
   1. get(A, i)

      return A[i]

   2. get(A, e)

      j = search(A, e)

      return A[j]

   3. get_max(A)

      [max, j] = search_max(A);

      return A[j];

   4. get_min(A)

      [min, j] = search_min(A);

      return A[j];

4. การลบข้อมูล เราทำการลบได้สี่แบบคือ ทราบตำแหน่ง ทราบค่า ลบค่าสูงที่สุด และลบค่าต่ำที่สุด
   1. delete(A, i)

      e = A[i];

      A[i] = A[--nA];

      return e

   2. delete(A, e)

      j = search(A, e)

      A[j] = A[--nA];

      return e

   3. delete_max(A)

      [max, j] = search_max(A);

      A[j] = A[--nA];

      return max

   4. delete_min(A)

      [min, j] = search_min(A);

      A[j] = A[--nA];

      return min

5. ทดสอบว่า array ว่างหรือไม่
   1. empty(A)

      return (nA == 0)

6. ทดสอบว่า array เต็มหรือไม่
   1. full(A)

      return (nA-1 == MAXARRAY)

7. ส่งจำนวนค่าใน array
   1. size(A)

      return nA

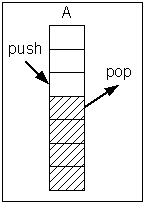
นิยามข้อมูลแบบกองซ้อน (Stack)
ข้อมูลแบบกองซ้อนมีคุณลักษณะคือ

1. มีจำนวนที่สำหรับเก็บข้อมูลจำกัด ต้องทราบจำนวนข้อมูลก่อนเริ่มใช้
2. ข้อมูลแต่ละตัวมักจะเป็นประเภทเดียวกัน และมีขนาดเท่ากัน
3. มีการเข้าถึงข้อมูลทางด้านเดียว (Top of Stack)

การกระทำบนข้อมูลแบบกองซ้อนประกอบด้วย:

1. insert an element = push(Stack, element)
2. search for an element in the list
3. retrieve an element and remove it = pop(Stack)
4. check if the stack is empty
5. check if the stack is full
6. find the number of elements

เราเขียนโครงสร้างข้อมูลกองซ้อนสำหรับจำนวนจริงได้ดังนี้

int MAXSTACK=100;

double S[MAXSTACK];

int tos=0;

1. การเติมข้อมูล
   1. push(S, e)

      if(not full(S)) then S[tos++] = e

2. การค้นหาข้อมูล
   เราแบ่งการค้นหาออกเป็นสามแบบ คือ การค้นหาสมาชิก e, การค้นหาค่าสูงสุดและการค้นหาค่าต่ำสุด
   1. search(S, e)

      create tempS

      j = 0;

      while(not empty(S))

      tempe = pop(S);

      push(tempS, tempe);

      if(e == tempe) then

          while(not empty(tempS))

              tempe = pop(tempS)

              push(S, tempe)

          return j

      j = j + 1;

      while(not empty(tempS))

      tempe = pop(tempS);

      push(S, tempe);

      return "not found"

   2. search_max(S)

      create tempS

      j = 0

      maxi = 0

      e = pop(S)

      push(tempS, e)

      while(not empty(S))

      tempe = pop(S)

      push(tempS, tempe)

      j = j + 1;

      if(e < tempe) then

          e = tempe

          maxi = j

      while(not empty(tempS))

      tempe = pop(tempS);

      push(S, tempe);

      return e, maxi

   3. search_min(S)

      create tempS

      j = 0

      mini = 0

      e = pop(S)

      push(tempS, e)

      while(not empty(S))

      tempe = pop(S)

      push(tempS, tempe)

      j = j + 1;

      if(e > tempe) then

          e = tempe

          mini = j

      while(not empty(tempS))

      tempe = pop(tempS);

      push(S, tempe);

      return e, mini

3. การเรียกข้อมูล
   เราแบ่งเป็นสี่แบบคือ ปกติ, ทราบตำแหน่งจาก tos, ค่าที่สูงที่สุด และค่าที่ต่ำที่สุด
   1. pop(S)

      return S[--tos]

   2. retrieve(S, i)

      create tempS

      j = 0;

      while(not empty(S))

      e = pop(S)

      push(tempS, e);

      if(j == i) then

          while(not empty(tempS))

              tempe = pop(tempS)

              push(S, tempe)

          return e;

      while(not empty(tempS))

      tempe = pop(tempS);

      push(S, tempe);

   3. get_max(S)

      [max, j] = search_max(S);

      return max;

   4. get_min(S)

      [min, j] = search_min(S);

      return min;

4. การลบข้อมูล เราทำการลบได้สี่แบบคือ ปกติ ทราบตำแหน่ง ลบค่าสูงที่สุด และลบค่าต่ำที่สุด
   1. pop(S)

      return S[--tos]

   2. pop(S, i)

      create tempS

      j = 0;

      while(not empty(S))

      e = pop(S)

      push(tempS, e);

      if(j == i) then

          pop(tempS)

          while(not empty(tempS))

              tempe = pop(tempS)

              push(S, tempe)

          return e;

      while(not empty(tempS))

      tempe = pop(tempS);

      push(S, tempe);

   3. pop_max(S)

      [max, j] = search_max(S);

      pop(S, j)

      return max

   4. pop_min(S)

      [min, j] = search_min(S);

      pop(S, j)

      return min

5. ทดสอบว่า stack ว่างหรือไม่
   1. empty(S)

      return (tos == 0)

6. ทดสอบว่า stack เต็มหรือไม่
   1. full(S)

      return (tos-1 == MAXSTACK)

7. ส่งจำนวนค่าใน stack
   1. size(S)

      return tos

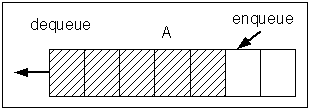
นิยามข้อมูลแบบแถวคอย (Queue)
ข้อมูลแบบแถวคอยมีคุณลักษณะคือ

1. มีจำนวนที่สำหรับเก็บข้อมูลจำกัด ต้องทราบจำนวนข้อมูลก่อนเริ่มใช้
2. ข้อมูลแต่ละตัวมักจะเป็นประเภทเดียวกัน และมีขนาดเท่ากัน
3. มีการเข้าถึงข้อมูลสองทาง (Head and Tail)

การกระทำบนข้อมูลแบบแถวคอยประกอบด้วย:

1. insert an element: enqueue(Queue, element)
2. search for an element in the list
3. retrieve an element and remove it: dequeue(Queue)
4. check if the queue is empty
5. check if the queue is full
6. find the number of elements

นิยามข้อมูลแบบรายการโยง(Linked list)
ข้อมูลแบบรายการโยงมีคุณลักษณะคือ

1. ใช้ตัวชี้ (pointer) ซึ่งสามารถขยายจำนวนข้อมูลอย่างไม่มีกำหนด (ข้อจำกัดขึ้นอยู่กับจำนวนหน่วยความจำที่มีทั้งหมด)
2. ข้อมูลแต่ละตัวมักจะเป็นประเภทเดียวกัน แต่สามารถมีขนาดที่ต่างกันได้
3. มีการเข้าถึงข้อมูลโดยการไล่ตามตัวชี้ (pointer)
4. สามารถเชื่อมโยงแบบทางเดียว หรือสองทางก็ได้

การกระทำบนข้อมูลแบบรายการโยงประกอบด้วย:

1. insert an element
2. search for an element in the list
3. retrieve an element
4. remove an element
5. check if the linked list is empty
6. find the number of elements

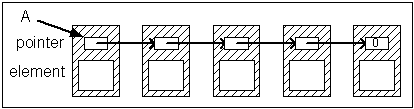(Linked list)
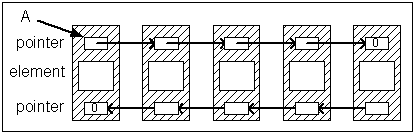(Doubly-linked list)
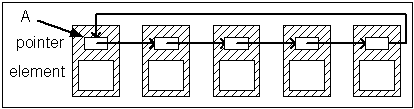(Circularly-Linked list)

นิยามข้อมูลแบบต้นไม้(Tree)
ข้อมูลแบบต้นไม้จะมีลักษณะเป็นกราฟ (Graph) ซึ่งสำหรับกราฟ จะมีความยุ่งยากและ ซับซ้อนในการจัดเก็บ เราจะสนใจการเก็บต้นไม้ในลักษณะของรายการโยงที่ไม่ใช่ linear ข้อมูลแบบต้นไม้มีคุณลักษณะคือ

1. ใช้ตัวชี้ (pointers) ที่มากกว่าหนึ่ง สามารถขยายจำนวนข้อมูลอย่างไม่มีกำหนด (ข้อจำกัดขึ้นอยู่กับจำนวนหน่วยความจำที่มีทั้งหมด)
2. ข้อมูลจะถูกเก็บไว้ที่ จุดต่อ (node) โดยจะมี จุดต่อราก (root node) เป็นจุดยอดที่สามารถเข้าถึงข้อมูลทุกค่าในต้นไม้ได้
3. ต้นไม้หนึ่งต้นจะต้องมีการเชื่อมโยงกันตลอด (connected)
4. ในแต่ละจุดต่อ (node) จะประกอบไปด้วยข้อมูลจริง และชุดของตัวชี้ (pointers) ซึ่งถ้ามีอยู่ 2 ตัวชี้ทั้งต้นก็จะถูกเรียกว่า binary tree หรือถ้ามีอยู่ 3 ตัวชี้ทั้งต้นก็จะถูกเรียกว่า ternary tree
5. ต้นไม้จะมีความสูง (height) ซึ่งนิยามเป็นจำนวนด้านที่มากที่สุดที่นับจาก จุดต่อรากมาถึงใบ (leaf) โดยที่ใบของต้นไม้คือ จุดต่อที่ไม่มี การแตกกิ่งออกจากจุดต่อนั้น
6. ความลึกของจุดต่อ (depth) นิยามเป็นจำนวนด้านทั้งหมดที่ใช้จาก จุดต่อรากจนถึงจุดต่อนั้น
7. ระดับของจุดต่อ (level) นิยามเป็นค่าของความสูงของต้นไม้ลบด้วยความลึกของจุดต่อนั้น
8. มีการเข้าถึงข้อมูลโดยการไล่ตามตัวชี้ (pointer) ซึ่งเรียกว่า tree traversals มีอยู่ 3 ประเภทคือ
   1. preorder traversal มีการกระทำที่จุดต่อนั้น ตามด้วยจุดต่อของต้นไม้ย่อยจากซ้ายไปขวา
   2. inorder traversal มีการกระทำจุดต่อของต้นไม้ย่อยทางซ้ายและตามด้วยจุดต่อนั้น แล้วจึงกระทำกับจุดต่อของต้นไม้ย่อยทางขวาไล่มา
   3. postorder traversal มีการกระทำจากจุดต่อของต้นไม้ย่อยจากซ้ายมาขวาและจบที่จุดต่อนั้น
   
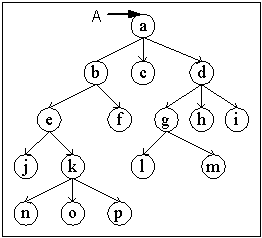
9. ต้นไม้มีคุณสมบัติพิเศษที่น่าสนใจคือ
   1. ต้นไม้ที่มี n จุดยอดจะมีกิ่งอยู่ n-1 กิ่ง
   2. ถ้ามีการเพิ่มด้านในต้นไม้โดยไม่มีการเพิ่มจุดยอด จะทำให้เกิดวัฏจักร (cycle) เพียงหนึ่งวัฏจักรและที่มีด้านนั้นเป็นด้านหนึ่งในวัฏจักร
   3. ถ้ามีการเอาด้านใดด้านหนึ่งออกจากต้นไม้ ต้นไม้ต้นนี้จะไม่มีการเชื่อมโยงในทุกจุดอีกต่อไปทำให้เกิดป่า (forest)

การกระทำบนข้อมูลแบบต้นไม้ประกอบด้วย:

1. insert an element
2. search for an element in the tree
3. retrieve an element
4. remove an element
5. check if the tree is empty
6. find the number of elements

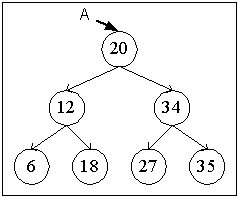(Tree)
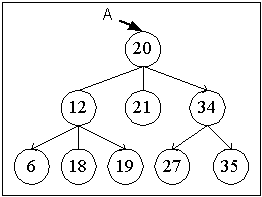(Ternary tree)
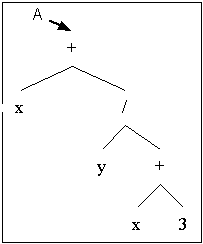(Binary tree)

นิยามข้อมูลแบบฮีป(Heap)
ข้อมูลแบบฮีปเป็นต้นไม้แบบทวิภาคบริบูรณ์ (Complete binary tree) ซึ่งจะเน้นการหาสมาชิกที่มีค่าน้อยที่สุด (มากที่สุด) และการเพิ่มสมาชิกในกองฮีป ข้อมูลแบบฮีปมีคุณลักษณะคือ

1. เป็นต้นไม้แบบทวิภาคบริบูรณ์ (Complete binary tree)
2. ข้อมูลที่อยู่ ณ จุดต่อใดๆ จะมีค่าน้อยกว่าหรือเท่ากับค่าของจุดต่อของต้นไม้ย่อยทั้งสองข้าง
3. ข้อมูลที่อยู่ที่จุดต่อรากจะมีค่าน้อยที่สุดเสมอ
4. มักใช้ ตัวแปรแบบแถวลำดับในการสร้างโดยสามารถคำนวณดรรชนีของลูกทางซ้าย (left child) และลูกทางขวา (right child) ได้ดังนี้
   1. ดรรชนีของจุดต่อที่เป็นจุดให้กำเนิด (parent) ของจุดต่อที่ดรรชนี n คำนวณได้จาก จำนวนเต็มที่มากที่สุดที่น้อยกว่าหรือเท่ากับ (n-1)/2
   2. ดรรชนีของลูกทางซ้ายของจุดต่อที่ดรรชนี n คำนวณได้จาก 2*n+1
   3. ดรรชนีของลูกทางขวาของจุดต่อที่ดรรชนี n คำนวณได้จาก 2*$n + 2

การกระทำบนข้อมูลแบบฮีปประกอบด้วย:

1. insert an element = $heap->add(element);
   • Heapup ปรับข้อมูลฮีปโดยพิจารณาจากปมนั้นขึ้นบน
   • Heapdown ปรับข้อมูลฮีปโดยพิจารณาจากปมนั้นลงมา (heapify)
2. retrieve the smallest element
3. remove the smallest element
4. merge two heaps
5. remove an element from the heap

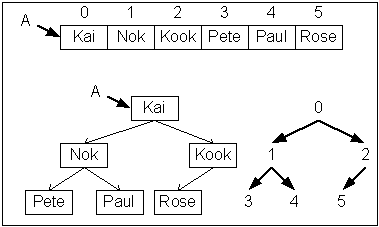
นิยามข้อมูลแบบแฮช(Hashing array)
ข้อมูลแบบแฮช เป็นข้อมูลในลักษณะแถวลำดับที่มีการใช้ดัชนีจากกลุ่มตัวอักขระ มีอีกชื่อหนึ่งที่นิยมใช้คือ associative array ข้อมูลแบบแฮชมีคุณลักษณะคือ

1. มีจำนวนที่สำหรับเก็บข้อมูลจำกัด ควรทราบจำนวนข้อมูลก่อนเริ่มใช้
2. ข้อมูลแต่ละตัวต้องมี key ซึ่งเป็นข้อมูลชนิดเดียวกัน สำหรับข้อมูลอื่นมีขนาดต่างกันได้
3. มีการเข้าถึงข้อมูลโดยการใช้ key

การกระทำบนข้อมูลแบบแฮชประกอบด้วย:

1. insert an element
2. retrieve an element
3. remove an element:
4. find the number of elements