- Recurrence equation
- Characteristic equation
- Homogeneous recurrences
- Inhomogeneous recurrences
นิยาม ความสัมพันธ์เวียนเกิด (Recurrence relation)
ความสัมพันธ์เวียนเกิดคือ การนิยามฟังก์ชันโดยใช้นิพจน์ที่มีความสัมพันธ์นั้นปรากฎอยู่
ตัวอย่างเช่น ลำดับ Fibonacci
F(n) = F(n-1) + F(n-2), F(1) = 1, F(2) = 1
ถ้าเราสามารถเขียน F(n) ในรูปแบบของฟังก์ชันอื่น ๆ ที่ไม่ขึ้นกับ F แล้วเราจะเรียกฟังก์ชันใหม่นั้นว่า
คำตอบของความสัมพันธ์เวียนเกิด
การแก้ความสัมพันธ์เวียนเกิด
- ประสบการณ์และการคาดคำตอบ (Intelligent guesswork)
วิธีการนี้ใช้การจำแนกและแยกแยะความสัมพันธ์โดยอาศัยประสบการณ์ ซึ่งแบ่งได้เป็น 4 ขั้นตอนดังนี้
1. คำนวณค่าตอนแรกมา 3-9 ค่า
2. ดูรูปแบบของเทอมและการเพิ่มขึ้นอย่างเป็นแบบแผน
3. คาดการณ์สูตรจากรูปแบบที่เกิดขึ้น
4. พิสูจน์โดยใช้อุปนัยคณิตศาสตร์ เพื่อยืนยันคำตอบ
ตัวอย่าง
T(n) = 3 T(n ÷ 2) + n ถ้า n 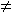 0, T(0) = 0
0, T(0) = 0
1. คำนวณค่าบางตัวสำหรับเลขที่หารสองลงตัว
| n |
1 | 2 |
4 | 8 |
16 | 32 |
| T(n) |
1 | 5 |
19 | 65 |
211 | 665 |
2. การดูรูปแบบ เราควรเขียนตารางข้างล่าง
| n | T(n) |
| 1 | 1 |
| 2 | 3 × 1 + 2 |
| 22 |
32 × 1 + 3 × 2 + 22 |
| 23 |
33 × 1 + 32 × 2 + 3 × 22 + 23 |
| 24 |
34 × 1 + 33 × 2 + 32 × 2 2
+ 3 × 23 + 24 |
| 25 |
35 × 1 + 34 × 2 + 33 × 2 2 +
32 × 2 3+ 3 × 24 + 25 |
3. เราจะได้สูตรว่า
T(2n) = 3n20 + 3n-121 + 3n-222 +
. . . + 31 × 2n-1 + 302n
= 3n 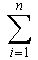 (2/3)i
= 3n+1 - 2n+1
(2/3)i
= 3n+1 - 2n+1
4. ทำให้อยู่ในรูป n จะได้
T(n) = T(2lg n) = 31 + lg n - 21 + lg n = 3 nlg 3 - 2 n
เมื่อ n = 2k
หลังจากนั้นเราจึงพิสูจน์โดยใช้อุปนัยคณิตศาสตร์
ความสัมพันธ์เวียนเกิดแบบเอกพันธุ์
อยู่ในรูป a0 tn + a1 tn-1 + . . . + ak tn-k = 0
มีคุณสมบัติ
- เชิงเส้น
- เอกพันธ์เพราะสัมประสิทธิ์ข้างหน้า tn-i เป็นการรวมเชิงเส้นที่มีค่าเป็นศูนย์
- สัมประสิทธิเป็นค่าคงตัว
เราพบว่า Fibonacci sequence สอดคล้องความสัมพันธ์เวียนเกิดแบบเอกพันธุ์ เพราะ
fn - fn-1 - fn-2 = 0
เราจะได้ข้อสังเกตว่าถ้า gn และ hn เป็นคำตอบแล้ว การรวมเชิงเส้นของ gn และ hn
จะเป็นคำตอบด้วยเสมอ นั่นคือ c gn + d hn เป็นคำตอบด้วย
ถ้าเราแทน tn ด้วย xn แล้วจะได้
a0 xn + a1 xn-1 + . . . + ak xn-k = 0
ซึ่ง x = 0 เป็นคำตอบหนึ่ง มิฉะนั้น หารตลอดด้วย xn-k
a0 xk + a1 xk-1 + . . . + ak = 0
เรียกว่า สมการลักษณะเฉพาะของความสัมพันธ์เวียนเกิด และเรียก
p(x) = a0 xk + a1 xk-1 + . . . + ak
ว่า พหุนามลักษณะเฉพาะ ซึ่งจะมีรากอยู่ k ราก เราสามารถเขียนได้ในรูปแบบ
p(x) = 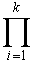 (x - ri)
ดังนั้น tn =
(x - ri)
ดังนั้น tn = 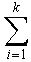 cirin
เป็นคำตอบของสมการด้วย
cirin
เป็นคำตอบของสมการด้วย
ตัวอย่าง(Fibonacci)
กำหนด fn = n ถ้า n = 0 หรือ n = 1
fn = fn-1 + fn-2 ในกรณีอื่น ๆ
เราสามรถเขียนได้เป็น fn - fn-1 - fn-2 = 0
พหุนามลักษณะเฉพาะคือ x2 - x - 1 ซึ่งมีคำตอบคือ r1 = 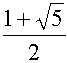 และ r2 =
และ r2 = 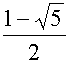 ดังนั้นคำตอบทั่วไปคือ
ดังนั้นคำตอบทั่วไปคือ
fn = c1 r1 + c2 r2
แก้สมการหาค่า c1 และ c2 จะได้
fn = 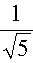 [ (
[ (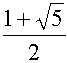 )n
- (
)n
- (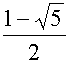 )n]
ความสัมพันธ์เวียนเกิดแบบไม่เอกพันธ์
)n]
ความสัมพันธ์เวียนเกิดแบบไม่เอกพันธ์
a0 tn + a1 tn-1 + . . . + ak tn-k = bn p(n)
มีคุณสมบัติ
- b เป็นค่าคงตัว
- p(n) เป็นโพลิโนเมียลฟังก์ชันของ n ระดับขั้น d
ตัวอย่าง
พิจารณา tn - 2 tn-1 = 3n
ในกรณีนี้ b = 3, p(n) = 1 สามารถแปลงเป็นสมการเอกพันธ์ได้
- คูณ 3: 3 tn - 6 tn-1 = 3n+1
- แทน n ด้วย n-1: 3 tn-1 - 6 tn-2 = 3n
- จาก 1 และ 2: tn - 5 tn-1 + 6tn-2 = 0
- พหุนามลักษณะเฉพาะ: x2 - 5x + 6 = (x-2)(x-3) = 0
- จะได้ tn = c1 2n + c23n
- แก้สมการ: c1 + c2 = t0, 2 c1 + 3 c2 = 2 t0 + 3
- c1 = t0 - 3, c2 = 3: tn = (t0 - 3)2n + 3n+1
ตัวอย่าง
พิจารณา tn - 2 tn-1 = (n + 5) 3n,
n  1
1
- เขียนความสัมพันธ์เวียนเกิด
- แทนค่า n ด้วย n - 1 แล้วคูณด้วย -6
- แทนค่า n ด้วย n - 2 แล้วคูณด้วย 9
- จะได้
| tn | - 2 tn-1 | | | = (n+5)3n |
| - 6 tn-1 | + 12 tn-2 | | = -6 (n+4) 3n-1 |
| | 9 tn-2 | - 18 tn-3 | = 9(n+3) 3n-2 |
- tn - 8 tn-1 + 21 tn-2 - 18 tn-3 = 0
- พหุนามลักษณะเฉพาะ: x3 - 8 x2 + 21 x - 18 = (x - 2)(x - 3)2 = 0
- จะได้ tn = c1 2n + c23n + c3 n 3n
- แก้สมการ: c1 + c2 = t0
2 c1 + 3 c2 + 3 c3 = 2 t0 + 18
4 c1 + 9 c2 + 18 c3 = 4 t0 + 99
- c1 = t0 - 9, c2 = 9, c3 = 3:
tn = (t0 - 9)2n + (n + 3) 3n+1
สรุป
สำหรับ
a0 tn + a1 tn-1 + . . . + ak tn-k = bn p(n)
เราสามารถใช้ พหุนามลักษณะเฉพาะ ในรูป
a0 xk + a1 xk-1 + . . . + ak)(x - b)d+1
ตัวอย่าง
พิจารณา tm = 2 tm-1 + 1, t0 = 0
อยู่ในรูป tm - 2 tm-1 = 1
- พหุนามลักษณะเฉพาะคือ (x - 2)(x - 1)
- tm = c1 1m + c2 2m
- แก้สมการ: c1 + c2 = 0, c1 + 2 c2 = 1
- c1 = -1, c2 = 1:
tm = 2m - 1
ตัวอย่าง
- จงหาคำตอบของความสัมพันธ์เวียนเกิด tn = 2 tn-1 + n, t0 = 1
- จงหาคำตอบของความสัมพันธ์เวียนเกิด tn = 4 tn-1 - 2n, t0 = 1
สรุป
สำหรับ
a0 tn + a1 tn-1 + . . . + ak tn-k =
b1n p1(n) + b2n p2(n) + . . .
เราสามารถใช้ พหุนามลักษณะเฉพาะ ในรูป
(a0 xk + a1 xk-1 + . . . + ak)(x - b1)d1+1
(x - b2)d2+1
ในการแก้ปัญหาได้เสมอ เมื่อ d1, d2, . . . คือระดับขั้นของ p1(n), p2(n), . . .
ตัวอย่าง
จงหาคำตอบของความสัมพันธ์เวียนเกิด tn = 2 tn-1 + n + 2n, t0 = 0
การเปลี่ยนตัวแปร
เราอาจเปลี่ยนตัวแปร n หรือ t
- T(n) = 3 T(n/2) + n เมื่อ n = 2k, T(1) = 1
- T(n) = 4 T(n/2) + n2
- T(n) = 2 T(n/2) + n lg n
- T(n) = L T(n/b) + c nk
จะได้ว่า 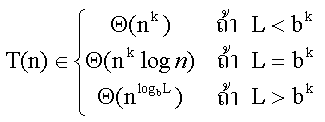
- T(n) = n T2(n/2), T(1) = 1/3