การวิเคราะห์กรณีที่แย่ที่สุด ดีที่สุดและกรณีเฉลี่ย (Worst-case, best-case and Average-case analysis)
เราพิจารณา Worst-case analysis ด้วยเหตุผลสามข้อ
- Worst-case running time เป็นขอบเขตด้านบนของเวลาที่ใช้ใน การทำงานสำหรับทุกข้อมูลเข้าที่เป็นไปได้ทั้งหมด
- ขั้นตอนวิธีบางประเภท เช่นการหาค่าในฐานข้อมูล database ซึ่งข้อมูลไม่อยู่ในฐานข้อมูล นั้น Worst-case
มักจะเกิดขึ้นบ่อย ๆ
- โดยทั่วไปแล้วกรณีเฉลี่ยมักจะใช้เวลานานพอ ๆ กับ Worst-case analysis
จากการวิเคราะห์ เราพบว่า Insertion Sort ใช้ Running time เป็น O(n2) ในกรณีที่แย่ที่สุด อย่างไรก็ตามถ้าเราพิจารณาในกรณี
ที่ดีที่สุดแล้ว เราพบว่า Insertion Sort ใช้ O(n) เราอาจสงสัยว่า ถ้าเราพิจารณาการจัดเรียงโดยเฉลี่ยแล้ว Insertion Sort จะมี Running time เป็นอย่างไร
การใช้กรณีเฉลี่ย เราจำเป็นต้องสมมติความน่าจะเป็นของตัวอย่างที่เกิดขึ้นซึ่งอาจมีการแจกแจงต่าง ๆ กันไป โดยทั่วไปแล้วเราจะใช้สมมติฐานที่ว่า
ตัวอย่างแต่ละตัวจะมีโอกาสเกิดขึ้นเท่า ๆ กัน สำหรับการจัดเรียงข้อมูลเราสมมติว่า โอกาสจะเกิดขึ้นของการจัดเรียงตัวเลข n ตัวเท่ากัน
ดังนั้นความน่าจะเป็นในการเกิดคือ 1/n!
เราสามารถหาคำตอบนี้ได้สองวิธี
- เราเพียงคำนวณหาเวลาที่ต้องใช้ในการเรียงของจำนวน permutation ทั้งหมดที่เป็นไปได้แล้วหารด้วย n!
- หรือ เราวิเคราะห์แต่ละกรณีของการจัดเรียงแบบ probabilistics แล้วจึงทำการบวกกัน
การจัดเรียงโดยใช้การเปรียบเทียบ Comparison sort
การจัดเรียงทั้งหมดที่ได้กล่าวมาเป็นการจัดเรียง โดยใช้การเปรียบเทียบระหว่างข้อมูลเป็นหลัก
นั่นคือสำหรับ a และ b เราใช้ผลของการเปรียบเทียบว่า a < b, a <= b, a = b, a >= b, a > b เป็นหลัก
โดยไม่มีข้อมูลส่วนอื่นช่วย สมมติว่าข้อมูลที่ต้องการนำมาจัดเรียงต่างกันทั้งหมด ดังนั้นเราจะเหลือการเปรียบเทียบแค่ a < b หรือ
a > b
ต้นไม้ของการตัดสินใจ Decision tree
เราเปรียบการจัดเรียงโดยการเปรียบเทียบ ให้เป็นต้นไม้ของการตัดสินใจได้ดังนี้
- แต่ละ internal node แทนด้วยการเปรียบเทียบระหว่างค่าของสองตัว ai: aj
- แต่ละกิ่งเป็นผลลัพธ์ของการเปรียบเทียบระหว่างค่าทั้งสอง
- แต่ละ leave node คือการจัดเรียงลำดับที่ถูกต้องของข้อมูล (Sorted by the permutation)
ดังนั้นการประมวลผลของโปรแกรมหรือขั้นตอนวิธีจะสอดคล้องกับ วิถี (path) จากจุดยอดของต้นไม้นี้ไปยัง ใบไม้(leaf)
เราต้องได้ว่าข้อมูลการเรียงทุกแบบเป็นใบไม้ ใบหนึ่งของต้นไม้ต้นนี้ เราต้องมีใบไม้อย่างน้อยที่สุด n!
ขอบเขตล่าง Lower bound
เราจะพบว่า วิถีที่ยาวที่สุดของต้นไม้ต้นหนึ่งคือจำนวนการเปรียบเทียบที่มากที่สุดของ Worst-case analysis
ดังนั้น จำนวนการเปรียบเทียบที่มากที่สุดที่เกิดขึ้น คือความสูงของต้นไม้ต้นนี้
ทบ. ต้นไม้ของตัดสินใจเพื่อการจัดเรียงข้อมูล n จำนวนมีความสูง
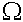 (n lg n) (n lg n)
บทแทรก Heap sort และ Merge sort เป็น optimal comparison sorts.
|