ขั้นตอนวิธีประเภทละโมภ (Greedy algorithm)
เป็นขั้นตอนวิธีการแก้ปัญหาที่คิดแบบง่าย ๆ และตรงไปตรงมา โดยพิจารณาว่าข้อมูลที่มีอยู่ในขณะนั้นมีทางเลือกใดที่
ให้ผลตอบแทนคุ้มที่สุด ขั้นตอนวิธีจะหาทางเลือกที่ดูดีที่สุดในขณะนั้นซึ่งถ้าข้อมูลนั้นพอเพียงที่จะทำให้สรุปคำตอบที่ดีที่สุด
เราจะได้ขั้นตอนวิธีที่มีประสิทธิภาพ โดยทั่วไปเราจะใช้ Greedy algorithm กับปัญหาเหมาะสมที่สุด Optimization problem เพราะว่า
เราต้องการการตัดสินใจว่าทางเลือกในปัจจุบันมีค่าตอบแทนมากที่สุดหรือน้อยที่สุดหรือไม่
ปัญหาการทอนเหรียญ
คนขายของผู้หนึ่งเปิดร้าน ขายของจิปาถะเล็ก ๆ เมื่อลูกค้าเข้ามาในร้านและซื้อสินค้าจากร้าน
ลูกค้ามักจะให้จำนวนเงินเป็นธนบัตรซึ่งมากกว่าราคาสินค้าจริง คนขายของต้องทอนเงินให้กับลูกค้า โดยทอนเป็นเหรียญ
กำหนดว่าเหรียญมีอยู่ห้าประเภทคือ เหรียญ dollar (มีค่า 100), เหรียญ quarter (มีค่า 25), เหรียญ dime (มีค่า 10), เหรียญ nickel (มีค่า 5)
และเหรียญ penny (มีค่า 1) ถ้าเขาต้องทอน x เขาจะให้เหรียญอย่างใดเท่าไร จึงจะมีจำนวนเหรียญที่ทอนให้น้อยที่สุด
ตัวอย่างเช่น $2.89 = 2 ของเหรียญ dollar + 3 ของเหรียญ quarter + 1 ของเหรียญ dime + 4 ของเหรียญ penny
MAKE-CHANGE(y)
ข้อมูลเข้า y เป็นจำนวนเต็มบวกหรือศูนย์
ข้อมูลออก (x5, x4, x3, x2, x1) เมื่อ x5 แทนจำนวนเหรียญ dollar, x4 แทนจำนวนเหรียญ quarter,
x3 แทนจำนวนเหรียญ dime, x2 แทนจำนวนเหรียญ nickel, x1 แทนจำนวนเหรียญ penny
โดยที่ x1, x2, x3, x4, x5 เป็นจำนวนเต็มบวกที่มากกว่าหรือเท่ากับศูนย์
1. C = (100, 25, 10, 5, 1);
2. x = (0,0,0,0,0);
3. sum = 0;
4. while sum != y do
5. i = largest in C such that sum + C[i]  y
6. if there is no such item then return "No solution";
7. (sum, x[i]) = (sum+C[i], x[i]+1);
8. endwhile
9. return x y
6. if there is no such item then return "No solution";
7. (sum, x[i]) = (sum+C[i], x[i]+1);
8. endwhile
9. return x
จงแสดงว่า ขั้นตอนวิธีที่ใช้ จะให้จำนวนเหรียญที่ทอนน้อยที่สุด
ทฤษฎี คำตอบ (x5, x4, x3, x2, x1) ที่ได้จาก MAKE-CHANGE algorithm ให้ผลเฉลยที่เหมาะที่สุด
พิสูจน์
- เราอ้างว่า MAKE-CHANGE จะมีคำตอบที่เหมาะที่สุดเสมอ เนื่องจาก
- สำหรับจำนวนเต็มบวก y ทุกจำนวน เรามีวิธีการทอนเหรียญอย่างน้อยหนึ่งแบบที่เป็นไปได้คือ การให้เหรียญ penny จำนวน y เหรียญ
- จำนวนเหรียญที่ต่ำที่สุดที่เป็นไปได้คือ 0 นั่นคือ เราจะมีขอบเขตล่างเสมอ
- เราเรียกคำตอบที่เหมาะที่สุดนั้นว่าคือ (z5, z4, z3, z2, z1)
- เราสามารถอ้างได้ว่า z5
 x5 เสมอ x5 เสมอ
สมมติว่า z5 < x5 หรือเขียนได้ว่า z5 + 1  x5. x5.
จากขั้นตอนวิธีที่เราเขียนขึ้น เราต้องได้ว่า จำนวนเงิน z5*100 + 100  y y
เราต้องทอนเหรียญให้ครบ 100 โดยใช้เพียงเหรียญ 25, 10, 5, 1 ซึ่งจะได้จำนวนเหรียญมากกว่า การทอนเหรียญเพียงเหรียญเดียวที่มีค่า 100 เสมอ
เราได้ว่า (z5, z4, z3, z2, z1) ไม่ใช่คำตอบที่เหมาะที่สุด เกิดการขัดแย้ง ดังนั้นที่สมมติไว้ไม่จริง
- โดยใช้หลักการพิสูจน์ที่คล้าย ๆ กัน จะได้ว่า z4
 x4,
z3 x4,
z3  x3, z2 x3, z2  x2,
z1 x2,
z1  x1, x1,
- ดังนั้น z5+z4+z3+z2+z1
 x5+x4+x3+x2+x1 x5+x4+x3+x2+x1
นั่นคือ (x5, x4, x3, x2, x1) มีจำนวนเหรียญในการทอนที่ต่ำที่สุด
รูปแบบโดยทั่วไปของขั้นตอนวิธีละโมภ สรุปได้ดังนี้
GREEDY(C: set): set
1. S = Ø
2. while C != Ø and not solution(S) do
3. x = select(C)
4. C = C - {x}
5. if feasible(S 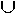 {x}) then S = S {x}) then S = S 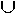 {x}
6. endwhile
7. if solution(S) then return S else return "No solution" {x}
6. endwhile
7. if solution(S) then return S else return "No solution"
ปัญหา Activity-selection problem
สมมุติว่าเรามีเซต S = {1, ..., n} เป็นเซตของ n activities ซึ่งต้องการใช้เครื่องจักรกลางในการประมวลผลขณะเวลาใด ๆ
โดยที่เครื่องจักรนี้ประมวลผลทีละ 1 activity ในขณะใด ๆ นั้นคือ ถ้า activity i ถูกประมวลผลอยู่แล้ว เราไม่สามารถประมวลผล activity อื่น ๆ ได้
สำหรับทุก activity i กำหนด si และ fi เป็นเวลาเริ่มต้นและเวลาสิ้นสุดในการประมวลผล โดยที่ si
 fi ในรูปแบบของ [si, fj) fi ในรูปแบบของ [si, fj)
เราเรียก i ว่าเข้ากับ j (compatible with j) ถ้า [si, fi) ไม่มีช่วงที่ร่วมกันกับ [sj, fj) นั้นคือ
si  fj หรือ sj fj หรือ sj
 fi
ดังนั้นปัญหา activity-selection คือการเลือกจำนวนของ activity ให้มากที่สุดจาก S โดยที่แต่ละ activity นั้นเข้ากันได้ทั้งหมด fi
ดังนั้นปัญหา activity-selection คือการเลือกจำนวนของ activity ให้มากที่สุดจาก S โดยที่แต่ละ activity นั้นเข้ากันได้ทั้งหมด
สมมติว่าข้อมูลที่เข้ามีการเรียง f1  f2 f2
 f3 f3  ... ...
 fn. fn.
ACTIVITY-SELECTOR(s, f)
ข้อมูลเข้า s และ f เป็น array ของจำนวนจริงบวกขนาด n โดยที่ si
 fi ทุก i fi ทุก i
ข้อมูลออก A เป็น stack ซึ่งเก็บดรรชนีของ activity ที่เลือก
1. n = length(s)
2. push(A, 1)
3. j = 1
4. for i = 2 to n do
5. if si  fj then
6. push(A, i)
7. j = i
8. return A fj then
6. push(A, i)
7. j = i
8. return A
s = (1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12), t = (4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14)
เราพบว่าขั้นตอนวิธีนี้ใช้หลักการของ greedy algorithm เพราะว่าเราสนใจเฉพาะ activity ที่เสร็จก่อน activity อื่น ๆ ทั้งหมด
ในเชิงปฏิบัติหลักการนี้จะพยายามเปิดช่องว่างในการเลือก activity ให้มากที่สุด
การพิสูจน์ความถูกต้องของ ACTIVITY-SELECTOR
ทฤษฎี ขั้นตอนวิธี ACTIVITY-SELECTOR ส่งคำตอบที่เลือกจำนวนของ activity ที่มากที่สุดใน S
โดยที่แต่ละ activity นั้นเข้ากันได้ทั้งหมด
พิสูจน์
- กำหนดให้ S = {1, 2, ..., n} โดยที่ ลำดับเรียงตาม fi
- เราต้องการจะแสดงว่าคำตอบที่เหมาะที่สุดมีอยู่หนึ่งคำตอบที่มี activity 1 อยู่ในเซตของคำตอบเสมอ
สมมติว่า A เป็นคำตอบที่เหมาะที่สุดของ S ที่กำหนดให้ เราสามารถสมมติโดยไม่เสียนัยว่า activity ใน A มีการเรียงลำดับของ fj
จากน้อยไปมาก
สมมติ activity แรกของ A เป็น k ถ้า k = 1 เราได้คำตอบอย่างที่ต้องการ
ถ้าไม่ใช่ เราต้องได้ f1  fk ดังนั้นเซตใหม่ที่เรากำหนดโดยตัด k ทิ้ง
และเติม 1 เข้าไปจะเป็นคำตอบที่เหมาะที่สุดด้วย เพราะว่าจำนวนของ activity เท่ากับ A (B = (A - {k}) fk ดังนั้นเซตใหม่ที่เรากำหนดโดยตัด k ทิ้ง
และเติม 1 เข้าไปจะเป็นคำตอบที่เหมาะที่สุดด้วย เพราะว่าจำนวนของ activity เท่ากับ A (B = (A - {k})
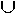 {1}) {1})
นั้นคือเราแสดงว่าจะมีคำตอบที่เหมาะที่สุดซึ่งมี activity 1 อยู่เสมอ
บทแทรก หลังจากเราเลือก 1 แล้วเราจะได้ว่าปัญหาที่เหลืออยู่จะเป็นปัญหา activity-selection ซึ่งมีขนาดเล็กลง
โดยที่ S ใหม่คือเซตของ activity ที่มี si  s1 โดยใช้ induction
เราจะได้ว่าคำตอบที่ได้จาก ACTIVITY-SELECTOR เป็นคำตอบที่เหมาะสมที่สุดตามต้องการ s1 โดยใช้ induction
เราจะได้ว่าคำตอบที่ได้จาก ACTIVITY-SELECTOR เป็นคำตอบที่เหมาะสมที่สุดตามต้องการ
ปัญหาการเลือกของ Knapsack problem โดยวิธีแบ่งส่วน
กำหนดให้มีของอยู่ n ประเภทและถุงอยู่หนึ่งถุง โดยที่ของประเภทที่ i มีน้ำหนักทั้งหมด wi อยู่ พร้อมค่า
vi เราไม่สามารถบรรทุกของเกิน W หน่วย เราต้องการเติมถุงนี้ให้เต็มโดยที่มีค่าผลรวมของ vi สูงที่สุดและน้ำหนักไม่เกินค่า
W ที่กำหนด
เราสามารถเขียนปัญหาให้อยู่ในรูปของ Optimization problem ดังนี้
- Maximize
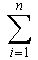 xi vi xi vi
- subject to
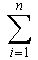 xi wi xi wi
 W W
- 0
 xi xi
 1 1
ขั้นตอนวิธีในการแก้ Knapsack problem
KNAPSACK
ข้อมูลเข้า w และ v เป็น array ของจำนวนจริงบวกขนาด n โดยที่ wi แทนน้ำหนักของของชิ้นที่ i,
vi แทนค่าของของชิ้นที่ i และ W เป็นน้ำหนักที่รองรับได้สูงสุด
ข้อมูลออก x เป็น array ของตัวเลขระหว่าง 0 กับ 1 ซึ่งบ่งบอกว่าเราต้องการของประเภทที่ i จำนวนเท่าใด
(1 หมายถึงทั้งหมด, 0 หมายถึงไม่เลือก และ 0.5 หมายถึงครึ่งหนึ่งเป็นต้น)
1. for i = 1 to n
2. x[i] = 0
3. weight = 0
4. while weight < W do
5. i = the best remaining object
6. if weight + w[i]  W then
7. x[i] = 1; weight = weight + w[i]
8. endif
9. endwhile
10. If weight != W then
11. i = the best remaining object
12. x[i] = (W-weight)/w[i]
13. endif
14. return x W then
7. x[i] = 1; weight = weight + w[i]
8. endif
9. endwhile
10. If weight != W then
11. i = the best remaining object
12. x[i] = (W-weight)/w[i]
13. endif
14. return x
ในขั้นตอนที่ 5 เราสามารถเลือกวิธีในการบ่งบอกว่า ของประเภทใดที่จะให้ค่าผลรวมดีที่สุด โดยที่เราอาจเลือกว่า
- เอาของที่ราคามากที่สุดก่อน
- เอาของที่มีน้ำหนักต่ำสุดก่อน
- เอาของที่มีอัตราส่วนระหว่าง vi / wi มากที่สุด
พิจารณาตัวอย่าง เรามีของ 5 ประเภทโดยที่แต่ละประเภทมีค่าดังนี้ 10, 20, 30, 40, 50 และน้ำหนัก 20, 30, 66, 40, 60 ตามลำดับ
โดยที่น้ำหนักทั้งหมดที่ใส่ถุงได้คือ 100
ทฤษฎี ขั้นตอนวิธี KNAPSACK จะให้คำตอบที่เหมาะที่สุด ถ้าการเลือกใช้หลักการเลือก vi/wi
จากมากไปหาน้อย และเราสามารถเลือกเพียงอัตราส่วนของแต่ละประเภท โดยกำหนดให้ค่าคิดตามอัตราส่วนของน้ำหนัก
ปัญหาการบริการลูกค้าให้มีเวลาในการรอน้อยที่สุด
กำหนดให้มีผู้บริการอยู่หนึ่งคน และมีลูกค้าอยู่ n คนโดยที่ เราทราบเวลาในการใช้บริการของลูกค้าแต่ละคนคือ t1,
..., tn เราต้องการหาเวลารวมในการรอที่น้อยที่สุดที่ลูกค้าต้องเสียไปในระหว่างรอรับบริการ จนรับบริการเสร็จ
ตัวอย่างเช่น เรามีลูกค้าอยู่สามคน โดยที่ t1 = 5, t2 = 10, t3 = 3
จงหาว่าเราต้องบริการลูกค้าอย่างไร จึงทำให้ผลรวมในการรอทั้งหมดน้อยที่สุด
ปัญหาการจัดตารางงานเมื่อมี deadline
เรามีงานอยู่ทั้งหมด n งานที่ใช้เวลาหนึ่งหน่วยในการทำ โดยที่ขณะเวลาใด ๆ เราสามารถทำงานได้เพียงงานเดียว
กำหนดว่า งาน i ให้ผลตอบแทน gi > 0 ก็ต่อเมื่อ งานนี้เสร็จไม่ช้าไปกว่าเวลา di
เราควรเลือกทำงานใด เมื่อไร เพื่อให้ได้ผลตอบแทนรวมสูงที่สุด
ตัวอย่างเช่น เรามีงาน 4 ชิ้นที่มีค่าตอบแทน 50, 10, 15, 30 และเวลาส่ง 2, 1, 2, 1 ตามลำดับ
ปัญหาการหา Minimum spanning tree
กำหนด G = < V, E > เป็นกราฟเชื่อมโยงซึ่งไม่มีทิศทาง เมื่อ V เป็นเซตของจุดยอด และ E เป็นเชตของด้าน
โดยกำหนดให้แต่ละด้านมีความยาวเป็นจำนวนเต็มบวก จงหาสับเซต T ของ E ซึ่งทำให้ทุกจุดยอดเชื่อมโยงกันและมีค่าผลรวมของทุกด้านน้อยที่สุด
- เนื่องจาก G เชื่อมโยงเราจะมี Minimum spanning tree เสมอ
- สำหรับกราฟเชื่อมโยงที่มี n จุดยอดต้องมีด้านมากกว่าหรือเท่ากับ n-1 เสมอ
- สำหรับกราฟที่มี n จุดยอดและมี n ด้านจะมี cycle ในกราฟนี้เสมอ
- ถ้า T มีจำนวนด้าน n-1 และสับกราฟ G เชื่อมโยง แล้วจะได้ว่า สับกราฟนี้คือต้นไม้
เราเรียกกราฟที่ได้ว่าเป็น minimum spanning tree ของ G ตัวอย่างของปัญหาที่ต้องการใช้ minimum spanning tree เช่น จุดยอดแต่ละจุดใน G แทนเมือง
และด้านแต่ละด้านคือการเชื่อมต่อของสายโทรศัพท์ โดยเรามีค่าใช้จ่ายในการวางสายที่เชื่อมระหว่างเมือง เราต้องการหาค่าใช้จ่ายที่ถูกที่สุดในการวาง
สายโทรศัพท์ โดยที่ทุกเมืองต้องเชื่อมโยงกัน
Kruskal algorithm
ข้อมูลเข้า G = (V, E) เป็นกราฟเชื่อมโยง และ l เป็นความยาวของแต่ละด้าน
ข้อมูลออก T เป็น minimum spanning tree ของกราฟ G
- Sort E by increasing length
- n = the number of nodes in V
- T = Ø
- Initialize n sets, each containing a different element of E
- repeat
- e = {u, v} = shortest edge not yet considered
- ucomp = find(u)
- vcomp = find(v)
- if ucomp != vcomp then
- merge(ucomp, vcomp)
- T = T
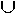 {e} {e}
- until T contains n - 1 edges
- return T
Prim's algorithm
ข้อมูลเข้า G = (V, E) เป็นกราฟเชื่อมโยง และ l เป็นความยาวของแต่ละด้าน
ข้อมูลออก T เป็น minimum spanning tree ของกราฟ G
- T = Ø
- B = {an arbitrary member of V}
- while B != V do
- find e = {u, v} of minimum length such that u
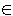 B and v B and v
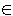 V - B V - B
- T = T
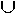 {e} {e}
- B = B
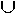 {v} {v}
- return T
ถ้าเราใช้ array mindist[] และ nearest[] ในการเขียนขั้นตอนวิธีของ Prim เราได้ว่า
Prim's algorithm
ข้อมูลเข้า G = (V, E) เป็นกราฟเชื่อมโยง และ l เป็นความยาวของแต่ละด้าน
ข้อมูลออก T เป็น minimum spanning tree ของกราฟ G
- T = Ø
- for i = 2 to n do
- nearest[i] = 1
- mindist[i] = L[i, 1]
- repeat n-1 times
- min =
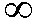
- for j = 2 to n do
- if 0
 mindist[j] < min then min = mindist[j]; k = j mindist[j] < min then min = mindist[j]; k = j
- T = T
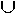 {{nearest[k], k}} {{nearest[k], k}}
- mindist[k] = -1
- for j = 2 to n do
- if L[j, k] < mindist[j] then
- mindist[j] = L[j, k]
- nearest[j] = k
- return T
Huffman codes
เป็นขั้นตอนวิธีการลดขนาดของข้อมูลที่มีจำนวนมากโดยที่สามารถนำข้อมูลแปลงกลับมาในสภาพที่เหมือนเดิมได้
โดยปกติสามารถลดขนาดของข้อมูลได้ 20% ถึง 90% หลักการคือการใช้ตารางความถี่การปรากฎของแต่ละตัวอักขระ
เพื่อหาวิธีการแทนที่ตัวหนังสือที่น้อยที่สุดโดยใช้ binary string
ถ้าเรามี 100,000 ตัวอักขระของข้อมูลโดยที่มีตัวอักขระที่ปรากฎอยู่ 6 ตัวเราจะได้ว่าโดยประมาณแล้วตัวอักขระ
แต่ละตัวจะปรากฎอยู่ 16667 ครั้ง ถ้าตัวอักขระแต่ละตัวใช้ fixed length code เราต้องใช้ 3 บิต ในการแทนที่ ตัวอักขระ
6 ตัว ดังนั้นจำนวนบิตทั้งหมดที่ต้องการ 300,000 บิต เช่น
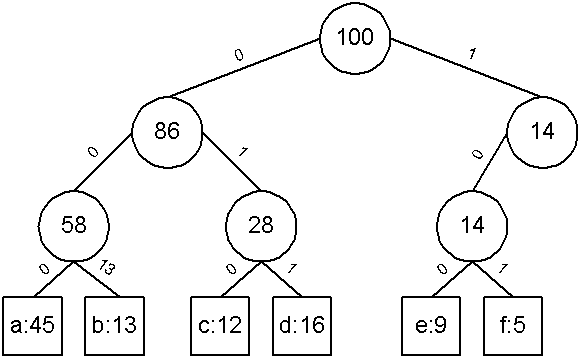
| a | b | c | d | e | f |
|---|
| Frequency | 45 | 13 | 12 | 16 | 9 | 5 |
| Fixed-length |
000 | 001 | 010 | 011 | 100 | 101 |
| Variable-length |
0 | 101 | 100 | 111 | 1101 | 1100 |
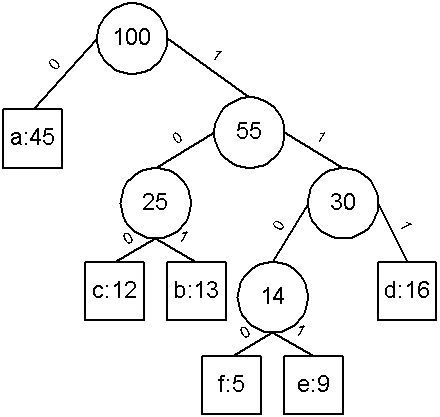
เราสามารถลดขนาดข้อมูลโดยใช้ variable-length code นั่นคือให้ตัวอักขระที่ความถี่มากที่สุดใช้จำนวนบิตที่น้อยที่สุด
จากตารางข้างต้นเราจะได้ว่าจำนวนบิตที่ต้องการคือ 224,000 บิต ซึ่งลดขนาดได้ประมาณ 25%
Prefix code
Prefix code คือการกำหนด code โดยที่รหัสที่ใช้แต่ละค่าไม่มีรหัสข้างหน้า (prefix) ซ้ำกับรหัสของ code อื่น ๆ
การสร้างข้อมูลโดยใช้รหัสที่กำหนด (encoding) สามารถทำได้โดยง่ายเมื่อทราบ prefix code นั่นคือเราแทนแต่ละ
ตัวอักขระด้วย code ที่กำหนดเขียนเรียงต่อกันจนจบเช่น abc แทนด้วย 0101100
ในทำนองเดียวกันการแปลงรหัสกลับ (decoding) สามารถทำได้ง่ายเมื่อทราบ prefix code เนื่องจากตัวอักขระทุกตัวไม่มีรหัสซ้ำกันข้างหน้า
ดังนั้นตัวอักขระจะไม่มีความกำกวม เราเพียงแค่จับคู่บิตกับรหัสที่มี เช่น 001011101 คือ aabe
เรานิยมใช้ binary tree ในการกำหนด prefix code โดยที่ leaf คือตัวอักขระ และ internal node แทนด้วยจำนวนข้อมูลที่สร้างต้นไม้
สำหรับแต่ละกิ่งจะแทนด้วย 0 หรือ 1 ซึ่งหมายถึงบิตที่จะใช้แทนรหัสของตัวอักขระโดยจะเรียงจาก root มายัง leaf
การสร้าง Huffman code tree
กำหนด tree ซึ่งแทน prefix code เราสามารถคำนวณจำนวนบิตที่ต้องใช้คือ
B(T) = 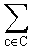 f(c) d(c, T) f(c) d(c, T)
เมื่อ f(c) แทนจำนวนความถี่ของตัวอักขระ c และ d(c, T) คือความสูงของตัวอักขระ c ใน T
เราจะใช้ค่า B(T) เป็นค่า cost ของต้นไม้ tree
Huffman code algorithm สร้างต้นไม้ซึ่งเป็น optimal prefix code
HUFFMAN-TREE(C, v)
ข้อมูลเข้า C เป็นเซตของตัวอักขระ n ตัว และ v เป็นจำนวนความถี่ของตัวอักขระแต่ละค่า
ข้อมูลออก รากของต้นไม้ prefix code
1. n = | C |
2. Q = C used v as a keyed
3. for i = 1 to n-1 do
4. z = ALLOCATE-NODE()
5. x = left[z] = Extract-Min(Q)
6. y = right[z] = Extract-Min(Q)
7. v[z] = v[x] + v[y]
8. Insert(Q, z)
9. return Extract-Min(Q)
ตัวอย่างเช่น C = {f, e, c, b, d, a}, v(f, e, c, b, d, a) = (5, 9, 12, 13, 16, 45)
เราพบว่าขั้นตอนวิธีนี้ใช้หลักการของ greedy algorithm เพราะว่าเราสร้างต้นไม้โดยเลือกค่าความถี่ที่น้อยที่สุด
การพิสูจน์ความถูกต้องของ Huffman code tree
ทฤษฎีย่อย กำหนด C เป็นเซตของตัวอักขระที่ปรากฎทั้งหมดและ v เป็นฟังก์ชันความถี่ของตัวอักขระแต่ละตัว
c ใน C ถ้า x และ y เป็นตัวอักขระสองตัวใน C ที่มีความถี่น้อยที่สุดในขณะนั้น แล้ว จะมี optimal prefix code ของ C สำหรับ x และ y ซึ่งมีขนาดเท่ากับ
x, y แต่ต่างกันที่บิตสุดท้าย
พิสูจน์ เราจะใช้หลักการที่ว่าสำหรับ Tree ที่ optimal tree เราจะสร้าง Huffman code tree ที่ optimal ที่มี x และ y ปรากฎเป็น
sibling leaves ที่มี maximum depth
กำหนดให้ b และ c เป็น sibling สองตัวที่มี maximum depth ใน T
เราสามารถสมมติโดยไม่เสียนัยว่า v[b]  v[c] และ v[x] v[c] และ v[x]
 v[y] จากการที่ v[x] และ v[y] เป็นความถี่ที่น้อยที่สุดจะได้ว่า v[x] v[y] จากการที่ v[x] และ v[y] เป็นความถี่ที่น้อยที่สุดจะได้ว่า v[x]
 v[b] และ v[y] v[b] และ v[y]  v[c] ดังรูป v[c] ดังรูป
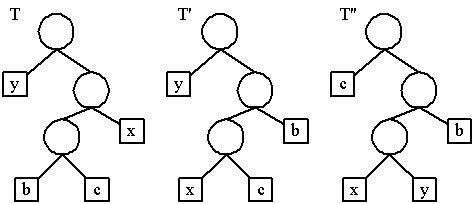
ขั้นแรก เราเปลี่ยนจาก T' เป็น T โดยสลับที่ระหว่าง b กับ x
ขั้นที่สอง เราเปลี่ยนจาก T' เป็น T" โดยสลับที่ระหว่าง c กับ y
เราจะได้
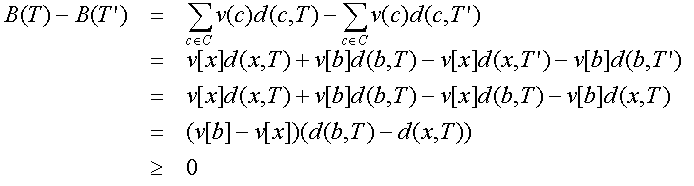
และในทำนองเดียวกัน เราจะได้ B(T') - B(T")  0
เราจะได้ว่า B(T") 0
เราจะได้ว่า B(T")  B(T) แต่ T เป็น optimal tree ดังนั้น T" เป็น optimal tree ด้วย B(T) แต่ T เป็น optimal tree ดังนั้น T" เป็น optimal tree ด้วย
ทฤษฎีย่อย ให้ T เป็น binary tree ซึ่งแทน optimal prefix code สำหรับ C และ v เป็นฟังก์ชันความถี่ของ C
สำหรับตัวอักขระสองตัว x และ y ซึ่งเป็น sibling leaves ของ T ที่มี z เป็น parent, ถ้า v[z] = v[x] + v[y] แล้วต้นไม้ T' = T - {x,y} เป็น
optimal prefix code ของ C' = C - {X, y}  {z} {z}
พิสูจน์ เนื่องจาก d(c, T) = d(c, T') ทุก c ใน C - {x, y} เราจะได้ v[c]d(c, T) = v[c] d(c, T')
เพราะว่า d(x, T) = d(y, T) = d(z, T') + 1 เราจะได้
v[x] d(x, T) + v[y] d(y, T) = (v[x] + v[y])(d(z, T') + 1) = v[z] d(z, T') + (v[x] + v[y])
ทำให้ได้ว่า B(T) = B(T') + v[x] + v[y]
ถ้า T' ไม่ใช่ optimal prefix code tree สำหรับ C' แล้วจะมี prefix code tree T" ซึ่ง B(T")  B(T')
เนื่องจาก z เป็นตัวอักขระตัวหนึ่งใน C' ดังนั้น z ต้องเป็น leaf หนึ่งใน T" และเมื่อเราเติม x และ y ลงไปเป็น
children ของ z ใน T" เราจะได้ว่า prefix code ของ C จะมี cost เป็น B(T") + v[x] + v[y] < B(T) เกิดการขัดแย้งกับ
optimality ของ T B(T')
เนื่องจาก z เป็นตัวอักขระตัวหนึ่งใน C' ดังนั้น z ต้องเป็น leaf หนึ่งใน T" และเมื่อเราเติม x และ y ลงไปเป็น
children ของ z ใน T" เราจะได้ว่า prefix code ของ C จะมี cost เป็น B(T") + v[x] + v[y] < B(T) เกิดการขัดแย้งกับ
optimality ของ T
ดังนั้นจะต้องได้ว่า T' ต้องเป็น optimal prefix code ของ C'
|