Tractable and intractable problems
Up to this point, we are normally interested in solving a computational problem by designing an efficient
algorithm. However, some problems are hard to find such an efficient algorithm and no known elegant efficient algorithm has been discovered yet.
In order to proceed the theory beyond this scope, we must have a rigorous approach to cope with these problems or identify them if necessary.
We call an algorithm the efficient algorithm if we can bound the running time of by the polynomial factor in term of its input size.
We say that the problem that has the efficient algorithm is tractable.
In other words, an algorithm is efficient if its running time is O(P(n)) where P(n) is a polynomial in the size of input n.
There are problems with no known polynomial-time algorithm. Some of these problems may be solved by efficient algorithms that are yet to be discovered.
However, many computer scientists believe that these problems cannot be solved efficiently. We will consider one special class of these problems called
NP-complete problem.
This special class has the property that there exists an efficient algorithm for any one NP-complete if and only if
there exist efficient algorithms for all NP-complete problems.
From this point, we will concentrate on the decision problems that is the problem with the yes or no answer.
This decision problem can be viewed as a language-recognition problem.
- Given a set of alphabets,
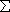 , we define the set of all possible strings from these alphabets
as , we define the set of all possible strings from these alphabets
as 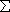 *. *.
- Let L
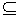 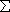 *
be the set of all strings for which the answer to the problem is yes. We call L the language corresponding to the problem. *
be the set of all strings for which the answer to the problem is yes. We call L the language corresponding to the problem.
Definition
- Let L1 and L2 be two languages from the input
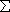 1*
and 1*
and 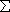 2*. We say that L1 is polynomially reducible to L2
if there exists a polynomial-time algorithm that converts each input w1 2*. We say that L1 is polynomially reducible to L2
if there exists a polynomial-time algorithm that converts each input w1 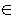
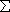 1* to another input w2 1* to another input w2 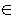
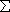 2* such that w1 2* such that w1 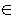 L1 if and only if w2
L1 if and only if w2 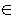 L2.
The algorithm is polynomial in the size of the input w1. L2.
The algorithm is polynomial in the size of the input w1.
The algorithm mentioned in the definition converts one problem to another. If we have an algorithm for L2, then we can compose the two algorithms to
produce an algorithm for L1.
- Denote the conversion algorithm by AC, and denote the algorithm for L2 by AL2.
- Given an arbitrary input w1 of
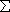 1* 1*
- We use AC to convert w1 to an input w2 of
 2* 2*
- We call AL2 to determine whether w2 belongs to L2 or not.
- If w2 is in L2 then w1 must be in L1.
Otherwise w2 is not in L2 then w1 is not in L1.
Polynomial-Time reductions
- Theorem 1
- If L1 is polynomially reducible to L2 and there is a polynomial-time algorithm for L2, then there is a polynomial
time algorithm for L1.
Note that the notion of reducibility is not symmetric. That is the L1 is polynomially reducible to L2 does not imply that L2 is
polynomial reducible to L1. This is because the definition only required that the input w1 of L1 can be converted into an
equivalent input of L2, but not vice versa. Hence, if L1 is polynomially reducible to L2, then we regard L2 to
be the harder problem.
Two languages L1 and L2 are polynomially equivalent or simply equivalent if each is polynomially reducible to the other.
- Theorem 2
- If L1 is polynomially reducible to L2 and L2 is polynomially reducible to L3 then L1
is polynomially reducible to L3
When we are given a problem that we cannot solve efficiently, we try to find whether it is equivalent to other problems that are known to be hard. Normally,
these hard problems are in the class of NP-complete.
Terminology
The theory of NP-completeness is a part of a large theory called computational complexity which we will not study here.
The NP-completeness is based on the fundamental model of computation such as Turing machine or a random access machine.
Note that it can be shown that those models of computations are equivalent for the purpose of the polynomial reduction. The NP is shorted handed for
the Nondeterministic Polynomial.
The nondeterminism is an abstract notion that will not be used or implemented the actual algorithm. We are only interested in the existence of
algorithms and problems in this class. A nondeterministic algorithm uses the same concept and notions of operations as the deterministic version. However,
it adds the nondeterministic choice (nd-choice). This nd-choice is used to handle (unknown) selection in order to solve the problem in polynomial time.
This choice must be limited. For each choice, the algorithm follows different computation path. We can assume without of loss of generality that the number of choice is
always two.
We say that the nondeterministic algorithm recognizes a language L if the following condition is satisfied:
- Given an input x, it is possible to convert each nd-choice encountered during the execution of the algorithm into a real choice such that
the outcome of the algorithm x will be accepted if and only if x
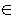 L. L.
In other word, if x is in the language, then the algorithm must provide at least one possible way to accept this input. However, to reject x,
the algorithm must reject all nd-choice paths.
Nondeterministic algorithms are very powerful, but their power is not unlimited. Not all problems can be solved efficiently by a nondeterministic algorithm.
For example, suppose the problem is to determine whether the maximum matching in a given graph. We can use the nondeterministic matching
algorithm to find a matching of size exactly k, but we cannot easily determine that there is no matching of a larger size.
The class of problems for which there exists a nondeterministic algorithm whose running time is polynomial in the size of the input is called NP.
One way to prove that a nondeterministic algorithms is powerful than the deterministic ones is to exhibit an NP problem that is not in the class P.
In contrast, if we want to prove that the two classed are equal (i.e., P = NP), then we have to show that every problem that belongs to NP can be solved by a
polynomial-time deterministic algorithm. Nobody has proved either of those directions. The problem of determining the relation between P and NP is known as the
P = NP problem.
- Definition
- A problem X is called an NP-hard problem if every problem in NP is polynomially reducible to X.
- Definition
- A problem X is called an NP-complete problem if
- X belongs to NP, and
- X is NP-hard.
The definition of NP-hardness implies that, if any NP-hard problem is ever proved to belong to P, then that proof would imply that P = NP.
Cook proved that there exists an NP-complete problem, (SAT). Once, we have found an NP-complete problem, proving that other problems
are also NP-complete becomes easier. Given a new problem Y, it is sufficient to prove that Cook's problem, or any other NP-complete problem,
is polynomially reducible to Y.
- Lemma 3
- A problem X is NP-complete problem if
- X belongs to NP, and
- Y is polynomially reducible to X, for some problem Y that is NP-complete.
Shortly after Cook's result became known, Karp found 24 important problems that he proved to be NP-complete. We will look at five examples of NP-complete problems.
Cook's theorem
The SAT problem is NP-complete.
- Let S be a boolean expression in conjunctive normal form (CNF). That is, S is the product (and) of several sums (or). For example,
S = (x + y + z')(x' + y + z)(x' + y' + z'), where addition and multiplication correspond to the
and and or boolean operations and each variable is either 0 (false) or 1 (true).
- A boolean expression is said to be satisfiable if there exists an assignment of 0s and 1s to its variables such that the value of the expression is 1.
- The SAT problem is to determine whether a given expression is satisfiable (without necessarily finding a satisfying assignment).
For example, the expression S above is satisfiable, since the assignment x = 1, y = 1 and z = 0 satisfy it. We call an assignment of 0s and 1s to the variables of a
boolean expression a truth assignment.
- The SAT problem is in NP because we can guess a truth assignment and check that it satisfies the expression in polynomial time.
- We will not show that it is NP-hard. But the idea is that the Turing machine and all of its operations on a given input can be described by a boolean expression.
This means that the expression will be satisfiable if and only if the Turing machine will terminate at an accepting state for the given input.
Examples of NP-Completeness proof
We will prove five problems are NP-complete from SAT. They are vertex cover, dominating set, 3SAT, 3-coloring, and clique.
- Vertex cover problem
- Given an undirected graph G = (V, E) and an integer k, determine whether G has a vertex cover containing
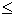 k. k.
For any undirected graph G = (V, E), a vertex cover of G is a set of vertices such that every edge in G is incident to at least one of these vertices.
- Dominating set problem
- Given an undirected graph G = (V, E) and an integer k, determine whether G has a dominating set containing
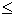 k. k.
For any undirected graph G = (V, E), a dominating set of G is a set of vertices in G such that every vertex of G is either in D or is adjacent to at least one
vertex from D.
- 3SAT problem
- Given a boolean expression in CNF such that each clause contains exactly three variables, determine whether is it satisfiable.
- Clique problem
- Given an undirected graph G = (V, E) and an integer k, determine whether G contains a clique of size
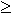 k. k.
For any undirected graph G = (V, E), a clique C in G is a subgraph of G such that all vertices in C are connected to all other vertices in C.
- 3-Coloring problem
- Given an undirected graph G = (V, E), determine whether G can be colored with three colors.
There are more NP-complete problems that are useful as a basis for other reductions.
- Hamiltonian cycle
- A Hamiltonian cycle in a graph is a simple cycle that contains each vertex exactly once. The problem is to determine whether a given graph
contains a Hamiltonian circuit. (Reduction from vertex cover.)
- Traveling salesman
- Let G = (V, E) be a weighted complete graph. A traveling salesman tour is a Hamiltonian cycle. The problem is to determine, given G and a number w,
whether there exists a traveling-salesman tour such that the total length of its edges is
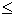 w. (Reduction from
Hamiltonian cycle.) w. (Reduction from
Hamiltonian cycle.)
- Hamiltonian path
- A Hamiltonian path in a graph is a simple open path that contains each vertex exactly once. The problem is to determine whether a given graph
contains a Hamiltonian path. (Reduction from vertex cover.)
- Independent set
- An independent set in an undirected graph G = (V, E) is a set of vertices no two of which are connected. The problem is to determine, given G and
an integer k, whether G contains an independent set with
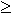 k vertices (Reduction from clique). k vertices (Reduction from clique).
- 3-dimensional matching
- Let X, Y and Z be disjoint sets of size k. Let M be a set of triples (x, y, z) such that x
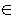 X,
y X,
y 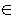 Y and z Y and z 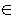 Z. The problem is to determine whether
there exists a subset of M that contains each element exactly once. (Reduction from 3SAT). Z. The problem is to determine whether
there exists a subset of M that contains each element exactly once. (Reduction from 3SAT).
- Partition
- The input is a set X such that each element x
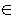 X has an associated size s(x). The problem is
to determine whether it is possible to partition the set into two subsets with exactly the same total size. (Reduction from 3-dimensional matching). X has an associated size s(x). The problem is
to determine whether it is possible to partition the set into two subsets with exactly the same total size. (Reduction from 3-dimensional matching).
- Knapsack
- The input is a set X such that each element x
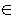 X has an associated size s(x) and value v(x).
The problem is to determine whether there is a subset B X has an associated size s(x) and value v(x).
The problem is to determine whether there is a subset B 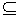 X whose total size is X whose total size is
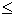 s and whose total value is s and whose total value is 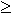 v. (Reduction from partition.) v. (Reduction from partition.)
- Bin packing
- The input is a sequence of numbers a1, a2, ..., an, and two other numbers b and k.
The problem is to determine whether the set can be partitioned into k subsets such that the sum of numbers in each subset is
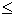 b. (Reduction from partition.) b. (Reduction from partition.)
|