Introduction
A mathematician and her husband are asked the following question:
"Suppose that you are in the basement and you want to boil water, what do you do?" The mathematician says
that she will go up to the kitchen and boil water there; her husband answers similarly.
Now they are both asked the following question: "Suppose that you are in the kitchen and you want to boil water,
what do you do now?" The husband says "It's easier -- I'll just fill the kettle and boil the water." The mathematician
answers "it's even easier than that -- I'll go down to the basement and I already know how to solve that problem."
Another example, when you send a package by Federal Express from uptown New York City to downtown
New York City, the package will be routed through Memphis. Federal Express routes all packages through Memphis,
so when they are faced with the special situation of delivering packages across town they "already know how to solve
the problem." In this case, the solution make sense. It may be much more difficult to identify a special situation and to
build a mechanism to handle that situation more efficiently. It may be easier, and overall cheaper, to handle everything
equally.
The notion of using the more general-purpose approach to solve a specific problem will not gain efficient of
the algorithm. However, it is easier to find the solution of the specific problem.
Consider we are given a problem P that seems complicated, but it is similar to a known problem Q. We have two choices
to solve this problem P.
- Solve the problem P directly by looking for the similarity of the problem Q and the method that uses to solve the problem Q.
- or try to change the input of the problem P into the input of the problem Q and then use the known algorithm to solve the problem Q
then change the output back to the solution of the problem P. This second approach is called a reduction (or transformation) between
two problems.
The purpose of using reduction is
- to find the solution of P that uses Q as a black box. This can be translated into an algorithm for P.
- if P is known to be hard problem with a known lower bound, then the same lower bound can be applied to the algorithm Q
For example, the problems of matrix multiplication and matrix squaring (i.e., multiplying the matrix by itself).
- It is clear that the squaring of a matrix can use the matrix multiplication algorithm to find the result. Therefore, the problem of
matrix squaring can be reduced to the problem of matrix multiplication.
- We can compute the matrix multiplication using the squaring of a matrix algorithm. In this case the matrix multiplication
can be reduced to matrix squaring problem. This second concept shows that computing the square of a matrix cannot be done faster than
computing the product of two arbitrary matrices.
An effective way to use reductions is to define a general problem to which many problems can be reduced. This problem must be
- general enough to cover a wide variety of problems,
- simple enough to have an efficient algorithm.
Examples of Reductions
We will study three examples of using reductions to obtain efficient algorithms.
- Simple string-matching problem
- Let A = a0a1...an-1 and B = b0b1...bn-1 be two strings of size n.
Determine whether B is a cyclic shift of A.
The problem is to determine whether there exists an index k such that ai = bk+i mod n for all i. We call this CSM
(Cyclic String Matching). The algorithm to solve this problem may be derived from
- naive approach, i.e., just match each element one by one and shift one at a time if not match;
- modified the Knuth-Morris-Pratt algorithm to solve this CSM;
- just reduce this CSM into the string matching problem and use the Knuth-Morris-Pratt algorithm to solve it.
The reduction would pose CSM as a regular instance of string matching problem. I.e., we look for a certain text T and a certain pattern P
such that finding P in T is equivalent to finding whether B is a cyclic shift of A.
The transformation is just set text T = AA (A concatenated to itself) and P = B. We have that B is a cyclic shift of A if and only if B is a substring of AA.
Since, we know how to solve the string matching problem in linear time, we have a linear time algorithm for CSM.
- Systems of distinct representatives
Let S1, S2, ..., Sk be a collection of sets. A system of distinct representatives (SDR) is a set R =
{r1, r2, ..., rk} such that ri
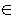 Si for all i.
Note that each ri must be distinct. In other words, R includes exactly one representative from each set. Si for all i.
Note that each ri must be distinct. In other words, R includes exactly one representative from each set.
- Consider the collections of S1 = {1, 2}, S2 = {2, 3, 4}, S3 = {1, 3} and S4 = {1, 2, 3}. Find the SDR for this collection.
- Consider the collections of S1 = {1, 2}, S2 = {2, 3, 4}, S3 = {1, 3}, S4 = {1, 2, 3} and S5 = {2, 3}.
Find the SDR for this collection.
- Given a finite collection of finite sets, find an SDR for the collection, or determine that none exists.
There is an elegant theorem due to P. Hall, that gives necessary and sufficient conditions for the existence of SDRs.
Let card(S) be the number of elements of S.
- Hall's theorem
- Let S1, S2, ..., Sk be a collection of sets. This collection has an SDR if and only if the following condition is satisfied:
- card(Si1
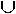 Si2 Si2 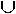 ...
... 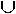 Sim) Sim) 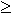 m m
- for every subset {i1, i2, ..., im} of {1, 2, 3, ..., k}.
To solve the SDR problem, we may use the following approaches.
- The naive approach, i.e., just try all possible subsets of elements from S1, S2, ..., Sk.
- Use the Hall's theorem, we must check all possible sub collections of S1, S2, ..., Sk.
- We reduce this SDR into the bipartite matching problem and use the bipartite matching algorithm to solve it.
The reduction would transform an instance of the SDR into a bipartite graph so that the finding SDR is equivalent to finding the matching in this bipartite graph.
The transformation is defined the graph G = (U 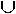 V, E) be a bipartite that U and V are disjoint vertices each
element in U is an element in the union of Si and element in V is the vertex vj corresponding to a set Sj. The edge is defined as
(vi, uj) V, E) be a bipartite that U and V are disjoint vertices each
element in U is an element in the union of Si and element in V is the vertex vj corresponding to a set Sj. The edge is defined as
(vi, uj)
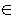 E if and only if uj E if and only if uj 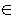 Si. Si.
We have the SDR {e1, e2, ..., ek} if and only if the corresponding assignment edges are matching of size k in this bipartite graph
and we know the algorithm to solve the bipartite matching.
The algorithm to solve the bipartite matching will based on the alternating-Path theorem
- A matching is maximum if and only if it has no alternating paths.
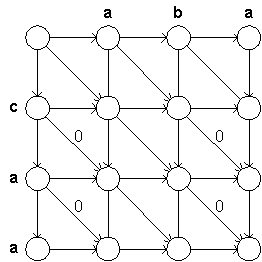
Given a bipartite graph G = (V 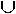 U, E), an alternating path P for a given matching M is a path from a vertex v in V
to a vertex u in U, both of which are unmatched in M, such that the edges of P are alternatively in E - M and in M. That means the first edge (v, w) of P does not
belong to M and the second edge (w, x) belongs to M, and so on. U, E), an alternating path P for a given matching M is a path from a vertex v in V
to a vertex u in U, both of which are unmatched in M, such that the edges of P are alternatively in E - M and in M. That means the first edge (v, w) of P does not
belong to M and the second edge (w, x) belongs to M, and so on.
- Sequence comparisons
Consider the sequence comparison problem: A = a1a2...an and B = b1b2...bm are two
strings of characters, and we want to edit A, character by character, until it becomes equal to B. We allow three types of edit steps, each involving one character.
- insert with the cost ci
- delete with the cost cd
- replace with the cost cr
The goal is to minimize the cost of the edit.
We can use the following approaches.
- The naive approach, i.e., just try to compute all possible editing sequence.
- Use the dynamic programming by constructing a table that each entry corresponds to the partial editing.
- Reduce this sequence comparison problem into the single source shortest path problem.
The reduction would transform an instance of the sequence comparison into a directed graph with the weight so that the editing sequence of the minimum cost
is equivalent to finding the shortest path from the initial state to the destination state.
The transformation is defined the entry from the partial editing as the vertex in the graph. There is an edge (v, w) if the partial edit corresponding to w has one more
edit step than the partial edit corresponding to v.
Consider the instance of the problem A = caa and B = aba. The horizontal edges correspond to insertions, the vertical edges to deletions,
and the diagonal edges to replacements. In the basic problem, the cost of each edge is 1 except for diagonal edges that correspond to equal characters.
Reductions involving linear programming
This section, we will consider the "super-problem" to which many problems can be reduced to. The important problem is the
linear programming. There are efficient algorithms for solving linear programming called the simplex method. We will consider the definition
of the standard linear programming problem and then shows the reductions from many problems to this super-problem.
We aim to maximize the objective function which is defined as the linear combination of a vector variable x =
(x1, x2, ..., xn) subject to the linear constraints. The objective function is defined as
- z :=
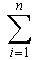 cixi cixi
where ci is a constant. The standard form of the linear programming will have the nonnegative constraints of variables together with
- Ai x = b.
For different inequality constraint such as 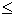 or or 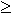 . We can
easily transform into the equality constraints by adding or subtracting the slack variable. . We can
easily transform into the equality constraints by adding or subtracting the slack variable.
Examples of reductions to linear programming
- The network flow problem
Let G = (V, E) be a directed graph with two distinguished vertices, s (the source) with in degree 0 and t (the sink) with out degree 0.
Each edge e in E has an associated positive weight c(e), called the capacity of e. The capacity measures the amount of flow
that can pass through an edge. We call such a graph a network. A flow is a function f on the edges of the network that
satisfies the following two conditions.
- 0
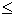 f(e) f(e) 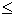 c(e): The
flow through an edge cannot exceed the capacity of that edge. c(e): The
flow through an edge cannot exceed the capacity of that edge.
- For all v
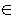 V - {s, t}, V - {s, t}, 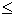 f(u, v) =
f(u, v) = 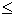 f(v, w): The total flow entering a vertex is equal to the total flow
exiting this vertex (except for the source and sink). f(v, w): The total flow entering a vertex is equal to the total flow
exiting this vertex (except for the source and sink).
These two conditions imply that the total flow leaving s is equal to the total flow entering t. The problem is to maximize this flow.
- Static Routing problem
Let G = (V, E) be an undirected graph representing a communication network. Suppose that each node vi in the network has a limited buffer
space, and can receive only Bi messages in one unit of time (we assume, for simplicity, that all messages have the same size). Suppose further
that there is no limit on the number of messages that can be transmitted through any link, and that each node has an infinite supply of messages. The problem
is to decide how many messages each edge should carry in one unit of time in order to maximize the total number of messages on the network.
- Philanthropist problem
Suppose there are n organizations that want to contributed money to k computer science departments. Each organization i has a limit of si
on its total contribution for the year, as well as a limit aij on the amount it is willing to contribute to department j (e.g. aij may be
0 for some departments). In general si is smaller than
 aij; therefore,
each organization has to make some choices. Furthermore, suppose that each department j has a limit of tj on the total amount of money it
can receive. The goal is to design an algorithm that maximizes the total contributions. aij; therefore,
each organization has to make some choices. Furthermore, suppose that each department j has a limit of tj on the total amount of money it
can receive. The goal is to design an algorithm that maximizes the total contributions.
- Assignment problem
Consider there are n workers and n jobs, we want to assign workers to do jobs. There is a cost associated with the worker i
doing the job j. The goal is to find the minimum cost for assigning workers to jobs.
|