ทฤษฎีการคณนา
ทฤษฎีการคณนาคือการศึกษาทฤษฎีที่เกี่ยวกับตัวแบบของการคำนวณของคอมพิวเตอร์ โดยพิจารณาสัญลักษณ์เข้า
ฟังก์ชันการเปลี่ยนสถานะและผลลัพธ์ที่ต้องการโดยใช้หลักทางคณิตศาสตร์และขั้นตอนวิธี (Algorithms)
ชื่ออื่นๆ ที่นิยมใช้กันเช่น Automata theory, Formal Language theory, Theory of Computation เป็นต้น
ประวัติ
ประโยชน์
- มีความเข้าใจ เรื่องตัวแบบคณนา
- สามารถนำตัวแบบคณนามาแก้ปัญหาได้
- ใช้อธิบายโครงสร้างของภาษา และนิพจน์ที่ภาษานั้นยอมรับได้
- ใช้ในการแก้ปัญหาตรรกะ เช่น ระบบการควบคุมหุ่นยนต์ (Control logic of Robot), ระบบตรรกของวงจร (Logic circuit) เป็นต้น
- สามารถ แสดงการพิสูจน์ว่า การทำงานของคอมพิวเตอร์ถูกต้องหรือไม่
- บอกระดับความยากของปัญหาที่พบ เช่น ปัญหาที่แก้ได้โดยใช้ออโตมาตาจำกัด (Finite Automata), ปัญหาที่แก้โดยใช้ออโตมาตาแบบกดลง
(Push-down automata), ปัญหาที่แก้ได้โดยใช้ เครื่องทัวริง (Turing Machine), ปัญหาที่ตัดสินไม่ได้ เป็นต้น
ทำไมเราควรเรียนวิชานี้
- เพื่อให้เข้าใจ หลักการการคำนวณของระบบคอมพิวเตอร์ ในเชิงนามธรรม
- เพื่อให้รู้จักภาษาต่าง ๆ ในเชิงทฤษฎีการคณนา เช่น ภาษาปกติ ภาษาไม่พึ่งบริบท เป็นต้น
- เพื่อให้เข้าใจหลักการ ตัวแบบคณนาในการแก้ปัญหาที่พบ
- เพื่อให้เข้าใจรูปแบบ การเขียนไวยากรณ์ต่างๆ ของภาษาคอมพิวเตอร์
- เพื่อให้รู้จักแบบฟอร์มมาตรฐานต่างๆ ของไวยากรณ์ เช่น รูปแบบ CNF, รูปแบบ GNF
- เพื่อให้สามารถแสดงความสัมพันธ์ต่างๆ ของตัวแบบคณนาได้
- เพื่อให้สามารถแสดงความยากง่ายของปัญหา โดยดูจากความซับซ้อนของการคณนา
- สามารถบอกระดับความยากของปัญหาในเชิงขั้นตอนวิธี
เซต
เซตคือกลุ่มของสิ่งต่าง ๆ ที่อยู่รวมกัน มักเขียนแทนด้วยอักษรภาษาอังกฤษตัวใหญ่เช่น A, B, C, D เป็นต้น
- สมาชิกของเซต ปกติเขียนแทนด้วยตัวอักษรภาษาอังกฤษตัวเล็ก เช่น a, b, c, d เป็นต้น
ถ้า a เป็นสมาชิกของเซต A เขียนแทนด้วย a
 A A
- การอธิบายเซต แบ่งได้เป็น
- การแจงสมาชิก เช่น A = {1, 2, 3, 4, ... }
- การบอกสมบัติของสมาชิกในเซต เช่น A = {x | x เป็นจำนวนเต็มบวก}
ทั้งนี้ เซตหนึ่งเซตอาจมีการบอกลักษณะที่แตกต่างกันได้มากมาย เช่น {1, 2, 3, 4, ... } เป็นเซตเดียวกับ {x | x เป็นจำนวนเต็มบวก} เป็นเซตเดียวกับ
{x | x เป็นจำนวนนับ}
- สัญลักษณ์ของเซตที่ควรทราบ
- เซตว่าง
 คือเซตที่ไม่มีสมาชิก คือเซตที่ไม่มีสมาชิก
- เซตของจำนวนนับ
 = {1, 2, 3, 4, 5, ...} = {1, 2, 3, 4, 5, ...}
- เซตของจำนวนเต็มบวกที่รวมศูนย์
 0 = {0, 1, 2, 3, 4, 5, ...} 0 = {0, 1, 2, 3, 4, 5, ...}
- เซตของจำนวนเต็ม
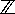 = {..., -3, -2, -1, 0, 1, 2, 3, ... } = {..., -3, -2, -1, 0, 1, 2, 3, ... }
- เซตของจำนวนตรรกยะ
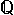 = {a/b | a = {a/b | a 
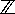 และ b และ b 
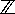 และ b และ b  0 } 0 }
- เซตของจำนวนจริง
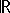
- ข้อตกลง สำหรับเซต A ใด ๆ
- จำนวนสมาชิกในเซต A เขียนแทนด้วย | A | เช่น | {a, b, c} | = 3, |
 | = 0 | = 0
- ตัวกระทำการบนเซต เรามักกำหนดเซตของสมาชิกที่เป็นไปได้ทั้งหมดคือ U เรียกว่า Universe เซต เรานิยามตัวกระทำการบนเซตได้ดังนี้
- ตัวกระทำการเอกภาค (Unary operator) ได้แก่
- ส่วนเติมเต็มของ A เขียนแทนด้วย A' หรือ AC หรือ
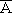 นิยามโดย
นิยามโดย 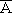 = {x = {x
 U | x U | x 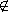 A }
เช่น ถ้า U = A }
เช่น ถ้า U =  แล้ว {1, 2}' = {3, 4, 5, ... } แล้ว {1, 2}' = {3, 4, 5, ... }
- ตัวกระทำการทวิภาค (Binary operator) ได้แก่
- ยูเนียนของเซต A กับเซต B เขียนแทนด้วย A
 B นิยามโดย
A B นิยามโดย
A  B = {x | x B = {x | x  A หรือ
x A หรือ
x  B } เช่น {1, 3, 5, 7, ... } B } เช่น {1, 3, 5, 7, ... }  {2, 4, 6, ... } = {1, 2, 3, 4, 5, ... }
{2, 4, 6, ... } = {1, 2, 3, 4, 5, ... }
- อินเตอร์เซกชันของเซต A กับเซต B เขียนแทนด้วย A
 B นิยามโดย
A B นิยามโดย
A  B = {x | x B = {x | x  A และ
x A และ
x  B } เช่น {1, 2, 3, 4, 5 } B } เช่น {1, 2, 3, 4, 5 }  {2, 4, 6, ... } = {2, 4 }
{2, 4, 6, ... } = {2, 4 }
- ผลต่างของเซต A กับเซต B เขียนแทนด้วย A - B นิยามโดย A - B = {x | x
 A แต่
x A แต่
x 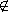 B } เช่น {1, 2, 3, 4, 5 } - {2, 4, 6, ... } = {1, 3, 5 } B } เช่น {1, 2, 3, 4, 5 } - {2, 4, 6, ... } = {1, 3, 5 }
- ผลต่อกันของเซต A กับ B เขียนแทนด้วย AB นิยามโดย AB = {xy | x
 A และ
y A และ
y  B } เช่น {0, 00, 000}{1} = {01, 001, 0001} B } เช่น {0, 00, 000}{1} = {01, 001, 0001}
- ผลคูณคาร์ทีเซียนของเซต A กับเซต B เขียนแทนด้วย A
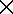 B นิยามโดย A B นิยามโดย A
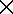 B = { (x, y) | x B = { (x, y) | x  A และ
y A และ
y  B } เช่น
{1, 2, 3} B } เช่น
{1, 2, 3} 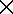 {2, 4} = { (1,2), (1,4), (2, 2), (2, 4), (3, 2), (3, 4) } {2, 4} = { (1,2), (1,4), (2, 2), (2, 4), (3, 2), (3, 4) }
- ตัวกระทำการกับชุดของเซต A1, ..., An
 Ai คือผลผนวกของชุดของเซต A1, ..., An
นิยามโดย Ai คือผลผนวกของชุดของเซต A1, ..., An
นิยามโดย  Ai = { x | Ai = { x | 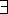 i i
 {1, 2, ..., n}, x {1, 2, ..., n}, x  Ai }
เช่น Ai = { i } จะได้ Ai }
เช่น Ai = { i } จะได้  Ai = {1, 2, 3, ..., n} Ai = {1, 2, 3, ..., n}
 Ai คือผลเหมือนของชุดของเซต A1, ...,
An นิยามโดย Ai คือผลเหมือนของชุดของเซต A1, ...,
An นิยามโดย  Ai = { x | Ai = { x |
 i i  {1, 2, ..., n}, x {1, 2, ..., n}, x
 Ai }
เช่น Ai = {1, 2, ..., i } จะได้ Ai }
เช่น Ai = {1, 2, ..., i } จะได้  Ai = {1 } Ai = {1 }
เราสามารถขยายกรณีที่ n ไม่จำกัดได้ในทำนองเดียวกัน
- การพิสูจน์เกี่ยวกับเซต เราสามารถแสดงการพิสูจน์เกี่ยวกับเซตได้โดยใช้หลักการสองแบบดังนี้
- การแสดงว่า A เป็นสับเซตของ B เขียนแทนด้วย A
 B
ซึ่งแสดงได้โดย B
ซึ่งแสดงได้โดย
กำหนดให้ x เป็นสมาชิกใด ๆ ถ้า x  A แล้วต้องสรุปให้ได้ว่า
x A แล้วต้องสรุปให้ได้ว่า
x  B B
เช่น {1}  
- การแสดงว่า A เป็นเซตเดียวกับเซต B เขียนแทนด้วย A = B ซึ่งแสดงได้โดย
การพิสูจน์ว่า A  B และ B B และ B  A A
ตัวอย่างเช่น {2, 4, 6, ... } = {x   |
x เป็นจำนวนคู่ }= {x |
x เป็นจำนวนคู่ }= {x   | |
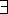 k k 
 , x = 2 k } , x = 2 k }
จากที่กล่าวมาเราสามารถสรุปความจริงเกี่ยวกับเซต ได้แก่
- | A
 B | B |  | A | + | B | | A | + | B |
- The commutative law: A
 B =
B B =
B  A และ
A A และ
A  B = B B = B  A A
- The associative laws: A
 ( B ( B
 C) = (A C) = (A  B) B)
 C C
และ
A  ( B ( B  C) =
(A C) =
(A  B) B)  C C
- The distributive laws: A
 ( B ( B
 C) = (A C) = (A  B) B)
 (A (A  C) C)
และ
A  ( B ( B  C) =
(A C) =
(A  B) B)  (A
(A  C) C)
- The idempotent laws: A
 A = A และ
A A = A และ
A  A = A A = A
- The absorptive laws: A
 ( A ( A
 B) = A และ
A B) = A และ
A  ( A ( A  B) = A B) = A
- The De Morgan laws: (A
 B)' =
A' B)' =
A'  B' และ (A B' และ (A  B)'
= A' B)'
= A'  B' B'
- กฎที่เกี่ยวกับส่วนเติมเต็ม: (
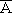 )' = A และ A )' = A และ A
 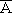 = Ø และ A = Ø และ A
 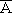 = U = U
- กฎที่เกี่ยวกับเซตว่าง : A
 Ø = A และ
A Ø = A และ
A  Ø = Ø Ø = Ø
- กฎที่เกี่ยวกับเซต Universe: A
 U = U และ
A U = U และ
A  U = A U = A
การพิสูจน์โดยใช้ตรรกศาสตร์
หลักการให้เหตุผล หรือ กฎการอนุมาน (Rule of inference) มีหลายกฎ แต่กฎที่เราใช้บ่อย ๆ คือ
Modus ponens ซึ่งกล่าวว่า ถ้าเรายอมรับข้อความ P  Q ว่าเป็นจริง และพบว่าข้อความ P
เป็นจริงแล้ว เราย่อมได้ว่า Q เป็นข้อความที่เป็นจริงด้วย
ในที่นี้ P และ Q เรียกว่าประพจน์ทางคณิตศาสตร์ หมายความว่าค่าความจริงของ P และ Q ที่ได้จะเป็นจริงหรือเท็จเท่านั้น Q ว่าเป็นจริง และพบว่าข้อความ P
เป็นจริงแล้ว เราย่อมได้ว่า Q เป็นข้อความที่เป็นจริงด้วย
ในที่นี้ P และ Q เรียกว่าประพจน์ทางคณิตศาสตร์ หมายความว่าค่าความจริงของ P และ Q ที่ได้จะเป็นจริงหรือเท็จเท่านั้น
กฎการอนุมาน
(Rule of inference) |
สัจนิรันดร์
(Tautology) |
ชื่อ |
ตัวอย่าง |
ทราบ p
สรุป p  q q |
p  (p (p  q) q)
|
Addition |
x = 0 สรุปได้ว่า x  0 0 |
ทราบ p  q q
สรุป p |
(p  q) q)  p p
|
Simplification |
x = 0 และ y > 0 สรุปได้ว่า x = 0 |
ทราบ p และ
ทราบ q
สรุป p  q q
|
(p)  (q) (q)  (p
(p  q) q)
|
Conjunction |
x = 0 และ z = 0 สรุปได้ว่า x และ z เท่ากับ 0 |
ทราบ p และ
ทราบ p  q q
สรุป q |
(p  (p (p  q)) q))
 q q
|
Modus ponens |
x = 2 และ ถ้า x  0 แล้ว จะมี x-1 ดังนั้น
สรุปได้ว่า 2 ที่ไม่ใช่ 0 จะมี 2-1 (คือ 1/2) 0 แล้ว จะมี x-1 ดังนั้น
สรุปได้ว่า 2 ที่ไม่ใช่ 0 จะมี 2-1 (คือ 1/2) |
ทราบ  q และ q และ
ทราบ p  q q
สรุป  p p |
( q q  (p
(p  q)) q)) 
 p p
|
Modus tollens |
ทราบว่า x ที่พบไม่มี x-1 และ ถ้า x  0
แล้ว จะมี x-1 เป็นจริง ดังนั้นสรุปได้ว่า x = 0 0
แล้ว จะมี x-1 เป็นจริง ดังนั้นสรุปได้ว่า x = 0 |
ทราบ p  q และ q และ
ทราบ q  r r
สรุป p  r r |
((p  q) q)  (q
(q  r)) r))  (p
(p  r) r)
|
Hypothetical
syllogism |
ทราบว่า ถ้า x = 2 แล้ว y = 4 และถ้า y = 4 แล้ว x + y = 6 จะสรุปได้ว่า ถ้า x = 2 แล้ว x + y = 6
|
ทราบ p  q และ q และ
ทราบ  p p
สรุป q |
((p  q) q) 
 p) p)  q q
|
Disjunctive
syllogism |
ทราบว่า x ที่พบ x  0 0
 x > 0 และ x เป็น 2 ซึ่ง x ไม่น้อยกว่าหรือเท่ากับ 0 แล้วเราสรุปได้ว่า x > 0 x > 0 และ x เป็น 2 ซึ่ง x ไม่น้อยกว่าหรือเท่ากับ 0 แล้วเราสรุปได้ว่า x > 0 |
ตัวอย่างการพิสูจน์ เช่นเราทราบว่า ถ้าจำนวนที่หารด้วย 9 ลงตัวแล้ว จำนวนนั้นจะหารด้วย 3 ลงตัวด้วย
- เราพบว่า 18 หารด้วย 9 ลงตัว จริง จาก Modus ponens เราสรุปได้ว่า 18 หารด้วย 3 ลงตัวด้วย
อย่างไรก็ตามเรามักสนใจ พิสูจน์ประโยคที่มีตัวแปรปรากฎอยู่ ตัวอย่างเช่น เราสนใจว่าข้อความ "ถ้า n หารด้วย 9 ลงตัวแล้ว n จะหารด้วย 3 ลงตัว
เป็นจริง สำหรับทุกค่าของ n ที่เป็นจำนวนนับ" ประโยคประเภทนี้ เรียกว่า ประโยคภาคแสดง (Predicate logic) ที่มีตัวขยาย quantifier คือ
ทุกค่าของ n
- ถ้าเรากำหนดให้ P(n) แทนข้อความ "ถ้า n หารด้วย 9 ลงตัวแล้ว n จะหารด้วย 3 ลงตัว"
- แล้ว เราต้องการจะพิสูจน์
 n P(n) สำหรับ n ที่เป็นจำนวนนับ n P(n) สำหรับ n ที่เป็นจำนวนนับ
ซึ่งการพิสูจน์ใช้กฎการอนุมานดังนี้
กฎการอนุมาน
(Rule of inference) |
ชื่อ |
ตัวอย่าง |
ทราบ  x P(x) x P(x)
สรุป P(c) เป็นจริงทุกค่าของ c |
Universal instantiation |
เราทราบว่า  x (x < 0 x (x < 0
 x x 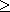 0) 0)
ดังนั้น 7 < 0
 7 7 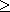 0 0 |
ทราบ P(c) เป็นจริงทุกค่าของ c ใน U
สรุป
 x P(x) x P(x) |
Universal generalization |
เราสามารถแสดงได้ว่า สำหรับ c ใด ๆ ที่เป็นจำนวนนับ c > 0 เราสามารถสรุปได้ว่า
 x x 
 , x > 0 , x > 0 |
ทราบ 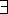 x P(x) x P(x)
สรุป P(c) เป็นจริงสำหรับบางค่าของ c |
Existential instantiation |
เราทราบว่า 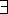 x x
 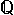 , 2 x = 1
ดังนั้นเราสรุปได้ว่า มีจำนวนตรรกยะ c (c = 1/2) ซึ่ง 2 c = 1 , 2 x = 1
ดังนั้นเราสรุปได้ว่า มีจำนวนตรรกยะ c (c = 1/2) ซึ่ง 2 c = 1 |
ทราบว่ามี c ซึ่งทำให้ P(c) เป็นจริง
สรุปได้ว่า
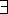 x P(x) x P(x) |
Existential generalization |
เรารู้ว่า 0 + y = y สำหรับทุก y ดังนั้นเราสามารถเขียนได้ว่า
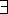 x x  y, x + y = y y, x + y = y
|
ความสัมพันธ์
ความสัมพันธ์คือเซตของคู่ลำดับ เราเรียก R เป็นความสัมพันธ์บนเซต A ก็ต่อเมื่อ R
 A A 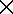 A
สมบัติของความสัมพันธ์ที่เราสนใจคือ A
สมบัติของความสัมพันธ์ที่เราสนใจคือ
- R มีสมบัติสะท้อน (reflexive) ก็ต่อเมื่อ
 x x
 A, (x, x) A, (x, x)  R หรือเขียนแทนด้วย x R x R หรือเขียนแทนด้วย x R x
- R มีสมบัติสมมาตร (symmetric) ก็ต่อเมื่อ
 x,
y x,
y  A, (x, y) A, (x, y)  R R
 (y, x) (y, x)  R R
- R มีสมบัติถ่ายทอด (transitive) ก็ต่อเมื่อ
 x, y, z x, y, z
 A, (x, y) A, (x, y)  R และ
(y, z) R และ
(y, z)  R R  (x, z)
(x, z)  R R
เรากล่าวว่า R เป็นความสัมพันธ์สมมูล (Equivalent relation) ก็ต่อเมื่อ R มีสมบัติทั้งสามแบบคือ สะท้อน สมมาตร และถ่ายทอด
ตัวอย่างของความสัมพันธ์
- จงพิจารณาว่าความสัมพันธ์ต่อไปนี้บนเซต A = {a, b} มีสมบัติสะท้อน สมมาตร และถ่ายทอดหรือไม่
- R1 = {(a, a)}
- R2 = {(a, b), (b, a)}
- R3 = {(a, a), (a, b), (b, a)}
- R4 = {(a, a), (a, b), (b, a), (b, b)}
- R5 =

- R6 = A
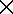 A A
- จงพิจารณาว่าความสัมพันธ์ต่อไปนี้บนเซต B = {ก, ข, ค} มีสมบัติสะท้อน สมมาตร และถ่ายทอดหรือไม่
- S1 = {(ก, ก), (ข,ข)}
- S2 = {(ก, ข), (ก, ก), (ข, ก)}
- S3 = {(ก, ข), (ก, ก), (ข, ก), (ข, ข)}
- S4 = {ก, ข}
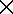 {ค} {ค}
- S5 =

- S6 = {ก, ข}
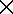 {ค} {ค}
- ความสัมพันธ์ของการลงรอยกันบนเซตของจำนวนเต็ม: กำหนด m เป็นจำนวนเต็มบวกใด ๆ
 a, b a, b 
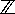 , a ลงรอยกับ b มอดุโล m ก็ต่อเมื่อ m หารผลต่าง b-a ได้ลงตัว , a ลงรอยกับ b มอดุโล m ก็ต่อเมื่อ m หารผลต่าง b-a ได้ลงตัว
เขียนแทนด้วย a  b (mod m) (a congruent to b modulo m)
จงพิสูจน์ว่าความสัมพันธ์นี้มี สมบัติสะท้อน สมมาตร และถ่ายทอดหรือไม่ b (mod m) (a congruent to b modulo m)
จงพิสูจน์ว่าความสัมพันธ์นี้มี สมบัติสะท้อน สมมาตร และถ่ายทอดหรือไม่
- พิจารณาว่าเซตต่อไปนี้มีสมบัติสะท้อน สมมาตร และถ่ายทอด
- R2 = {(a, b) | a
 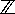 และ
b และ
b  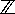 และ
a และ
a  b (mod 2)} b (mod 2)}
- R4 = {(a, b) | a
 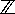 และ
b และ
b  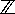 และ
a และ
a  b (mod 4)} b (mod 4)}
- R8 = {(a, b) | a
 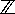 และ
b และ
b  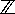 และ
a และ
a  b (mod 8)} b (mod 8)}
ความสัมพันธ์โคลเชอร์: ให้ p เป็นสมบัติของความสัมพันธ์, R และ S เป็นความสัมพันธ์บนเซต A เรากล่าวว่า
- S เป็นโคลเชอร์ของ R ที่มีสมบัติ p (p-closure of R) ก็ต่อเมื่อ S เป็นความสัมพันธ์บนเซต A ที่เล็กที่สุดที่มีคุณสมบัติ p และ
R
 S S
เรากำหนดว่า
- R+ คือโคลเชอร์ของ R ที่มีสมบัติถ่ายทอด
- R* คือโคลเชอร์ของ r ที่มีสมบัติสะท้อน และถ่ายทอด
ตัวอย่างของความสัมพันธ์โคลเชอร์
ให้ A = {1, 2, 3} และ R = {(1, 2), (2, 2), (2, 3)} จงพิจารณาว่าความสัมพันธ์ใดต่อไปนี้ เป็นโคลเชอร์ของ R ที่มีสมบัติสะท้อน
สมมาตร และถ่ายทอด
- S1 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)}
- S2 = {(1, 2), (2, 2), (2, 3), (1, 3)}
- S3 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}
- S4 =

- S5 = A
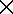 A A
สำหรับความสัมพันธ์ R ใด ๆ บนเซต A, (x, y)  R+ ก็ต่อเมื่อ
(x, y) ต้องสอดคล้องสมบัติสองข้อต่อไปนี้เท่านั้น R+ ก็ต่อเมื่อ
(x, y) ต้องสอดคล้องสมบัติสองข้อต่อไปนี้เท่านั้น
- (x, y)
 R R  (x, y)
(x, y)  R+ R+
- (x, y)
 R+ และ (y, z) R+ และ (y, z)  R+
R+  (x, z) (x, z)  R+ R+
สำหรับความสัมพันธ์ R ใด ๆ บนเซต A, R* = R+  {(a, a) | a
{(a, a) | a  A} A}
การแบ่งกั้น
ถ้า R เป็นความสัมพันธ์สมมูลบนเซต A แล้ว R แบ่งกั้น (partition) เซต A ออกเป็นเซตต่างสมาชิก (disjoint set) โดยที่แต่ละเซตไม่ใช่เซตว่าง
และผลยูเนียน (union) ของเซตเหล่านั้นทั้งหมดเท่ากับเซต A โดยเราจะเรียก เซตเหล่านั้นว่า เซตชั้นสมมูล (Equivalence class)
ตัวอย่าง จงหาเซตของชั้นสมมูลของความสัมพันธ์ต่อไปนี้บนเซต 
- R2 = {(a, b) | a
 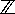 และ
b และ
b  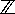 และ
a และ
a  b (mod 2)} b (mod 2)}
- R4 = {(a, b) | a
 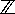 และ
b และ
b  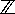 และ
a และ
a  b (mod 4)} b (mod 4)}
- R8 = {(a, b) | a
  และ
b และ
b   และ
a และ
a  b (mod 8)} b (mod 8)}
การพิสูจน์โดยอุปนัยเชิงคณิตศาสตร์
อุปนัยเชิงคณิตศาสตร์ (Mathematical Induction) คือการพิสูจน์สำหรับประโยคที่มีตัวแปรมีค่าเป็นจำนวนนับเท่านั้น
โดยการพิสูจน์อาศัยหลักที่ว่า ประโยคเริ่มต้นเป็นจริง (คือ P(1) เป็นจริง) และถ้าเราสามารถแสดงว่า การพิสูจน์ค่าความจริงของประโยค P(n+1)
เกิดจากค่าความจริงของประโยค P(n) เราจะได้ว่า P(n) เป็นจริงทุกค่าของ n ที่เป็นจำนวนนับ
พิจารณาปัญหาต่อไปนี้
- 1. สูตรทั่วไปของการบวกตัวเลขจาก 1 ถึง n มีหรือไม่ ถ้ามีคืออะไร พิสูจน์อย่างไร
- 2. สูตรทั่วไปของการบวกตัวเลขคี่จาก 1 ถึง n มีหรือไม่ ถ้ามีคืออะไร พิสูจน์อย่างไร
- 3. สูตรทั่วไปของการบวกตัวเลขคู่จาก 1 ถึง n มีหรือไม่ ถ้ามีคืออะไร พิสูจน์อย่างไร
อุปนัยเชิงคณิตศาสตร์ : ให้ P(n) แทนข้อความสำหรับจำนวนนับ n ใด ๆ
1. แสดงได้ว่า P(1) เป็นจริง
2. สมมติว่า P(k) เป็นจริง แล้วแสดงได้ว่า P(k+1) เป็นจริง
จะได้ว่า P(n) เป็นจริงทุกจำนวนนับ n ที่เป็นไปได้
เราเรียก ประโยคในข้อ 1. ว่า มูลฐานของการอุปนัย (basis of induction) และ ประโยคข้อ 2. ว่า ขั้นอุปนัย (inductive step)
และเรียกสมมติฐานในประโยคข้อ 2. ที่ว่า P(k) เป็นจริงว่า สมมติฐานของการอุปนัย (inductive hypothesis)
ตัวอย่างที่ 1 จงพิสูจน์ว่า
- 12 + 22 + 32 + . . . + n2 = n(2n+1)(n+1)/6
- 1 + 3 + 5 + 7 + . . . + (2 n - 1) = n2
- n < 2n
- n3 - n หารด้วย 3 ลงตัว
- 1 + 2 + 22 + . . . + 2n = 2n+1 - 1
- 1 + 2 + 3 + . . . + n = n (n + 1)/2
- 2n < n! สำหรับทุก n > 3
- 8 + 13 + 18 + 23 + ... + (3 + 5n) = 2.5 n2 + 5.5 n
- 1/2 + 1/4 + ... + 1/2n < 1
- xn - yn หารด้วย x - y ลงตัวทุกค่าของจำนวนนับ x, y, n ที่ x ไม่เท่ากับ y
- จงหาผลบวกของ 1/2 + 1/4 + ... + 1/2n แล้วแสดงการพิสูจน์
- 12 - 22 + 32 - 42 + ... + (-1)k-1k2 =
(-1)k-1k(k+1)/2
- จงหาผลบวกของ 1 × 2 + 2 × 3 + ... + n × (n+1) พร้อมแสดงการพิสูจน์
- 1/(n+1) + 1/(n+2) + ... + 1/(2n) > 13/24 สำหรับ n > 1
- กำหนดให้ 1+x > 0 จงแสดงว่า (1+x)n
 1 + n x 1 + n x
- กำหนดตัวเลขที่เขียนแทนด้วยเลขฐานสิบ เช่น 3241 เรียกตัวเลขนี้ว่า x
- x หาร 9 ลงตัว ก็ต่อเมื่อ ผลบวกของตัวเลขโดดทุกตัว หาร 9 ลงตัว
- x หาร 3 ลงตัว ก็ต่อเมื่อ ผลบวกของตัวเลขโดดทุกตัว หาร 3 ลงตัว
- จงพิสูจน์หลักการรังนกพิราบ (pigeonhole principle) ซึ่งกำหนดว่า นกพิราบ n + 1 ตัว เมื่อเข้ารัง n รัง จะได้ว่ามีอย่างน้อยหนึ่งรังที่มีนก
มากกว่าหนึ่งตัว
อุปนัยเชิงคณิตศาสตร์แบบเข้ม
ให้ P(n) แทนข้อความสำหรับจำนวนนับ n
1. แสดงได้ว่า P(1) เป็นจริง
2. สำหรับจำนวนเต็มบวก k ถ้า P(1), P(2), P(3), ..., P(k) เป็นจริง แล้ว ทำให้พิสูจน์ได้ว่า P(k+1) เป็นจริง
จะได้ว่า P(n) เป็นจริงทุกจำนวนนับ n
ตัวอย่างที่ 2 จงพิสูจน์ว่า
- an < (7/4)n เมื่อกำหนดให้ a1 = 1, a2 = 3 และ
an = an-1 + an-2 สำหรับ n > 2
- จงแสดงว่า จำนวนค่าของแสตมป์ที่มากกว่า 12 บาท สามารถใช้แสตมป์ดวงละ 4 บาทและ 5 บาทเท่านั้นในการรวมกัน
- จงแสดงว่า สำหรับจำนวนนับ n ใด ๆ จะมีจำนวนเต็ม a และ b ที่ทำให้ n = 2 a + 3 b เสมอ
กราฟ ไดกราฟ กราฟหลายด้าน กราฟเทียมและต้นไม้
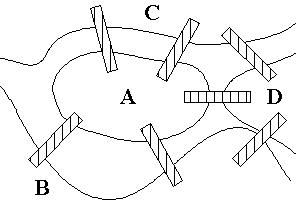
จากบันทึกที่ทราบ กราฟถูกใช้ครั้งแรกโดย Leonhard Euler เพื่อใช้ในการแก้ปัญหา Königsberg bridge โดยที่
ชาวเมืองต้องการทราบว่า มีทางเป็นไปได้หรือไม่ที่จะข้ามสะพาน 7 สะพานที่เชื่อมระหว่างเกาะดังรูปเพียงครั้งเดียว
โดยที่ไม่มีการข้ามสะพานซ้ำกันเลย
นอกจากนี้เรานำกราฟมาใช้แก้ปัญหา การวางแผงวงจรบน planar circuit board, การแยกความแตกต่างของโมเลกุลสองชนิดที่มี
โครงสร้างต่างกัน แต่มีอนุภาคเท่ากัน, การตรวจสอบว่าคอมพิวเตอร์สองเครื่องเชื่อมต่อกันบนเครือข่ายโดยใช้ตัวแบบกราฟของระบบเครือข่าย,
การหาระยะทางที่สั้นที่สุดระหว่างเมืองสองเมือง เป็นต้น
กราฟ คือคู่ลำดับของเซตสองเซต G = (V, E) โดยที่ V แทนเซตจำกัดของจุดยอด (vertex) และ E แทนเซตจำกัดของด้าน
(edge) เราแบ่งกราฟได้เป็นหลายประเภทดังนี้
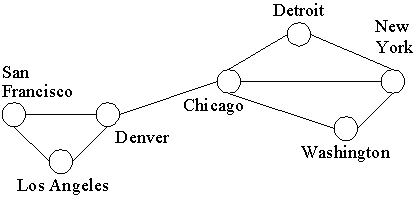
- กราฟอย่างง่าย (simple graph) คือกราฟที่มีด้านเชื่อมระหว่างจุดยอดสองจุด ที่ไม่มีทิศทาง กำหนดโดย G = (V, E) และ
E = { {u, v} | u
 V และ v V และ v  V และ
u V และ
u  v}
ตัวอย่างเช่น v}
ตัวอย่างเช่น
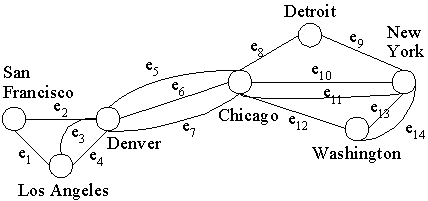
- กราฟหลายด้าน (multigraph) คือกราฟที่มีด้านเชื่อมระหว่างจุดยอดสองจุดใด ๆ มีได้มากกว่าหนึ่งด้าน กำหนดโดย G = (V, E) และ
E = {e1, e2, ..., em} และมีฟังก์ชัน f ซึ่ง f : E
 { {u, v} | u
{ {u, v} | u  V และ v V และ v  V โดยที่
u V โดยที่
u  v } กล่าวคือ ค่าของ f จะบอกว่า ด้าน ei เชื่อมระหว่างจุดยอดสองจุดใด
ตัวอย่างเช่น v } กล่าวคือ ค่าของ f จะบอกว่า ด้าน ei เชื่อมระหว่างจุดยอดสองจุดใด
ตัวอย่างเช่น
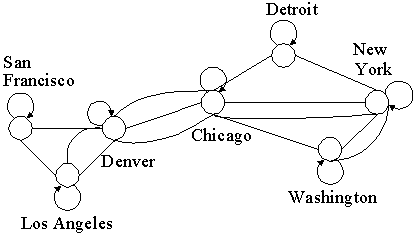
- กราฟเทียม (pseudograph) คือกราฟที่มีด้านเชื่อมระหว่างจุดยอดใด ๆ โดยอนุญาติให้ด้านสามารถเชื่อมต่อระหว่างจุดยอดเดียวกันได้
อาจมีทิศทางหรือไม่มีทิศทางก็ได้ กำหนดโดย G = (V, E) และ E = {e1, e2, ..., em} และมีฟังก์ชัน f ซึ่ง
f : E
 { {u, v} | u { {u, v} | u  V และ
v V และ
v  V } ตัวอย่างเช่น V } ตัวอย่างเช่น
- ไดกราฟ (digraph หรือ directed graph) คือกราฟที่มีด้านเชื่อมระหว่างจุดยอดใด ๆ แบบมีทิศทาง กำหนดโดย G = (V, E) และ
E = { (u, v) | u
 V และ v V และ v  V โดยที่
u V โดยที่
u  v} ตัวอย่างเช่น v} ตัวอย่างเช่น

- ไดกราฟหลายด้าน (directed multigraph) คือกราฟที่มีด้านเชื่อมระหว่างจุดยอดใด ๆ ได้มากกว่าหนึ่งแบบมีทิศทาง โดย G = (V, E)
และ E = {e1, e2, ..., em} และมีฟังก์ชัน f ซึ่ง
f : E  { (u, v) | u
{ (u, v) | u  V และ v V และ v  V โดยที่
u V โดยที่
u  v } กล่าวคือ
f บอกว่า ด้าน ei เชื่อมจากจุดยอดใด ไปจุดยอดใด แบบมีทิศทาง ตัวอย่างเช่น v } กล่าวคือ
f บอกว่า ด้าน ei เชื่อมจากจุดยอดใด ไปจุดยอดใด แบบมีทิศทาง ตัวอย่างเช่น
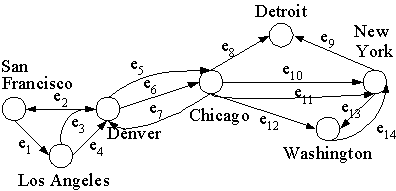
- สำหรับ f(e) = (v, w) เราเรียก v ว่าจุดยอดนำหน้า (predecessor) ของ w และ w ว่าจุดยอดตามหลัง (successor) ของ v
ตัวอย่างที่ 3
- กำหนดให้ G = (V, E) โดยที่ V = {1, 2, 3}, E = {e1, e2, e3, e4} มีฟังก์ชัน f ดังนี้
f(e1) = (1,3), f(e2) = (3,1), f(e3) = (3,2), f(e4) = (3,3) เราเขียนกราฟเทียมแบบมีทิศทางได้ดังนี้
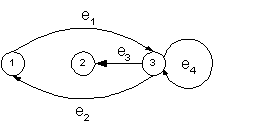
- จงวาดกราฟเทียมแบบมีทิศทางของ G = (V, E) โดยที่ V = {a, b, c, d}, E = {e1, e2, e3,
e4, e5} มีฟังก์ชัน f ดังนี้ f(e1) = (a,b), f(e2) = (b,c), f(e3) = (c,a), f(e4)
= (c,d), f(e5) = (d,d)
นิยามของกราฟที่ควรทราบ
กำหนดให้ G = (V, E) เป็นกราฟเทียมแบบมีทิศทาง
- ทางเดิน (walk) จากจุดยอด v1 ไป vn คือลำดับของจุดยอด v1 , v2, ..., vn
ใน V ซึ่ง (v1, v2), ..., (vn-1, vn) เป็นด้าน ด้านหนึ่งใน E เขียนแทนด้วย
v1 v2 ... vn
- วิถี (path) คือทางเดินที่ทุกด้านต่างกันทั้งหมด
- วัฎจักร (cycle) คือทางเดินจากจุดยอดจุดหนึ่งกลับมาจุดยอดเดิม โดยไม่มีด้านซ้ำ
ต้นไม้ (tree) เป็นสับเซตของไดกราฟ ซึ่ง
1. มีจุดยอดพิเศษอยู่หนึ่งจุดเรียกว่าราก (root) ที่ไม่มีจุดยอดนำหน้าและมีวิถี (path) จากจุดยอดนี้ไปยังทุกจุดของกราฟ
2. ไม่มีวัฎจักรในกราฟ
เราเรียกจุดยอดทุกจุดที่ไม่มีด้าน ออกจากจุดยอดนั้นว่าใบไม้ (leaf)
ตัวอย่างที่ 4
- กำหนดให้ G = (V, E) โดยที่ V = {1, 2, 3, 4, 5, 6, 7} , E = {(1,2), (1,3), (3,4), (3,5), (3,6), (6,7)}
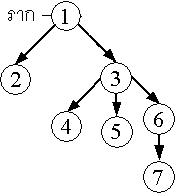
- กำหนดให้ G = (V, E) โดยที่ V = {a, b, c} , E = {(a,b), (c,a), (c,b)} จงตรวจสอบว่า G เป็นต้นไม้หรือไม่
โดยปกติ เราไม่นิยมเขียนลูกศรแสดงทิศทางใน กราฟต้นไม้ เนื่องจากเราทราบทิศทางที่แน่นอนอยู่แล้ว
ชุดตัวอักขระและภาษา
ชุดตัวอักขระ (alphabet) คือ เซตจำกัดของสัญลักษณ์ที่ไม่ใช่เซตว่าง เขียนแทนด้วย
 เช่น เช่น  = {0, 1} = {0, 1}
เรานิยาม การกระทำที่เกี่ยวกับ ตัวอักขระได้ดังนี้
- สายอักขระ (string) จาก
 คือลำดับจำกัดของสัญลักษณ์จาก คือลำดับจำกัดของสัญลักษณ์จาก
 ซึ่งเขียนติดกัน เช่น ccddd เป็นต้น นิยมใช้ตัวอักษรภาษาอังกฤษเขียนแทนเช่น u, v, w, x, y, z ซึ่งเขียนติดกัน เช่น ccddd เป็นต้น นิยมใช้ตัวอักษรภาษาอังกฤษเขียนแทนเช่น u, v, w, x, y, z
- ความยาว (length) ของสายอักขระ w เขียนแทนด้วย |w| คือจำนวนตัวอักขระที่ปรากฎทั้งหมดใน w เช่น |ccddd| = 5 หรือ
w = ccdd แล้ว |w| = 4
- สายอักขระผันกลับ (reverse) ของ w เขียนแทนด้วย wR คือ สายอักขระที่เกิดจาก w โดยผันกลับจากขวาสุดมาซ้ายสุด เช่น
w = ccdd แล้ว wR = ddcc
- สายอักขระว่าง (empty string) เขียนแทนด้วย
 หรือ หรือ
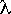 คือสายอักขระที่ไม่มีสัญลักษณ์ปรากฎอยู่เลย เราได้ว่า
| คือสายอักขระที่ไม่มีสัญลักษณ์ปรากฎอยู่เลย เราได้ว่า
| | = 0 | = 0
- การต่อกันของ wx คือการนำสายอักขระ w มาเขียนต่อกัน (concatenate) กับ x
เรียก w ว่าสายอักขระเติมหน้า (prefix) ของ x และ x เรียกสายอักขระต่อท้าย (suffix) ของ w
- wn = w w . . . w เมื่อ n เป็นจำนวนเต็มบวกที่มากกว่า 1 และนิยาม
w0 =
 และ w1 = w
และ w1 = w
- v เป็นสายอักขระย่อย (substring) ของ w เมื่อมีสายอักขระ u และ z ที่ w = u v z
 * คือเซตของสายอักขระทั้งหมดจาก * คือเซตของสายอักขระทั้งหมดจาก
 รวม รวม 
-
 + = + =
 * - { * - { } }
- L เป็นภาษา (language) จาก
 ก็ต่อเมื่อ
L ก็ต่อเมื่อ
L   * *
เช่น  , {c, d}, { , {c, d}, { , cd} ต่างก็เป็นภาษาจาก , cd} ต่างก็เป็นภาษาจาก

- สมาชิกทุกตัวในภาษา L เรียกว่าคำ (word) หรือประโยค (sentence) ใน L
ข้อสังเกต ภาษาก็คือเซต
คอมพลีเมนต์ (Complement)
กำหนดให้  เป็นชุดตัวอักษร และ L, L" เป็นภาษาจาก เป็นชุดตัวอักษร และ L, L" เป็นภาษาจาก

- คอมพลีเมนต์ (complement) ของ L เทียบกับ
 *
เขียนด้วย *
เขียนด้วย 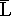 คือ คือ
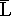 = =  * - L
= {w * - L
= {w   * |
w * |
w 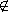 L } L }
- ภาษาผันกลับ (reverse) ของ L เขียนแทนด้วย LR คือ
- LR = {wR | w
 L} L}
- การต่อกัน (concatenation) ของ L และ L" เขียนแทนด้วย LL" คือ
- LL" = { x y | x
 L และ y L และ y  L" } L" }
ดังนั้น Ln = L L L . . . L เมื่อ n เป็นจำนวนเต็มบวกตั้งแต่ 2 ขึ้นไป และในกรณี n = 0 และ n = 1 เรานิยาม
L0 = { }และ L1 = L }และ L1 = L
L* = L0  L1
L1  L2
L2  . . . = . . . =
 Ln และ Ln และ
L+ = L1  L2
L2  L3
L3  . . . = . . . =
 Ln Ln
ตัวอย่างที่ 5
- กำหนดให้
 = {a, b} และ
L1 = {a, aa, ab} จงหา L1R, = {a, b} และ
L1 = {a, aa, ab} จงหา L1R, 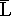 1, L12,
L13, L1*, L1+ 1, L12,
L13, L1*, L1+
- กำหนดให้
 = {0, 1} และ
L2 = {0n | n เป็นจำนวนคี่บวก} = {0, 000, 00000, ...} จงหา L2R, = {0, 1} และ
L2 = {0n | n เป็นจำนวนคี่บวก} = {0, 000, 00000, ...} จงหา L2R, 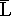 2,
L22, L23, L2*, L2+ 2,
L22, L23, L2*, L2+
- กำหนดให้
 = {0, 1} และ
L3 = {x = {0, 1} และ
L3 = {x   * | x มีจำนวนศูนย์เท่ากับจำนวนหนึ่ง}
จงหา L3R, * | x มีจำนวนศูนย์เท่ากับจำนวนหนึ่ง}
จงหา L3R, 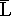 3, L32, L33,
L3*, L3+ 3, L32, L33,
L3*, L3+
- กำหนดให้
 = {0, 1} และ
L4 = {x = {0, 1} และ
L4 = {x   * | x แทนด้วยเลขฐานสองที่หารด้วย
3 ลงตัว} จงหา L4R, * | x แทนด้วยเลขฐานสองที่หารด้วย
3 ลงตัว} จงหา L4R, 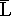 4, L42, L43,
L4*, L4+ 4, L42, L43,
L4*, L4+
- กำหนดให้
 = {0, 1} และ
L5 = {0n1n | n = {0, 1} และ
L5 = {0n1n | n   0}
จงหา L5R, 0}
จงหา L5R, 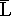 5, L52, L53,
L5*, L5+ 5, L52, L53,
L5*, L5+
- กำหนดให้
 = {0, 1} และ
L6 = {xxR | x = {0, 1} และ
L6 = {xxR | x   *}
จงหา L6R, *}
จงหา L6R, 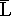 6, L62, L63,
L6*, L6+ 6, L62, L63,
L6*, L6+
- กำหนดให้
 = {0, 1} และ
L7 = {x = {0, 1} และ
L7 = {x   * | x = xR}
จงหา L7R, * | x = xR}
จงหา L7R, 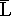 7, L72, L73,
L7*, L7+ 7, L72, L73,
L7*, L7+
- กำหนดให้
 = {0, 1} และ
L8 = {0n1m | n > m = {0, 1} และ
L8 = {0n1m | n > m 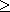 0}
จงหา L8R, 0}
จงหา L8R, 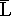 8, L82, L83,
L8*, L8+ 8, L82, L83,
L8*, L8+
- กำหนดให้
 = {0, 1} และ
L9 = {0n1m | n = 2 m, n = {0, 1} และ
L9 = {0n1m | n = 2 m, n   0}
จงหา L9R, 0}
จงหา L9R, 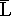 9, L92, L93,
L9*, L9+ 9, L92, L93,
L9*, L9+
- กำหนดให้
 = {0, 1} และ
L10 = {0n1n0n | n = {0, 1} และ
L10 = {0n1n0n | n   0}
จงหา L10R, 0}
จงหา L10R, 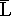 10, L102, L103,
L10*, L10+ 10, L102, L103,
L10*, L10+
- กำหนดให้
 = {0, 1} และ
L11 = {ww | w = {0, 1} และ
L11 = {ww | w   *}
จงหา L11R, *}
จงหา L11R, 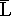 11, L112, L113,
L11*, L11+ 11, L112, L113,
L11*, L11+
- กำหนดให้
 = {0, 1} และ
L12 = { 0n | n เป็นจำนวนเฉพาะ}
จงหา L12R, = {0, 1} และ
L12 = { 0n | n เป็นจำนวนเฉพาะ}
จงหา L12R, 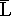 12, L122, L123,
L12*, L12+ 12, L122, L123,
L12*, L12+
|