คือเครื่องมือหรืออุปกรณ์คำนวณชนิดหนึ่งซึ่งมีหน่วยความจำจำกัด (ใช้สถานะจำกัดในการจดจำ) และรับข้อมูลโดยการอ่านแถบบันทึกรับเข้า โดยที่อุปกรณ์ชนิดนี้จะให้คำตอบว่าสายอักขระที่อยู่ในแถบบันทึกรับเข้านั้นยอมรับได้หรือไม่ได้ ดังรูป

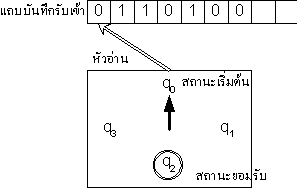
เราจะนิยามอุปกรณ์ชนิดนี้เชิงคณิตศาสตร์เพื่อความชัดเจนในการพิสูจน์ และการนำไปใช้

ออโตมาตาจำกัดเชิงกำหนด (Deterministic Finite Automata)

นิยาม ออโตมาตาจำกัดเชิงกำหนด (Deterministic Finite Automata หรือ DFA) ประกอบด้วย

1. Q แทน เซตของสถานะทั้งหมด (a set of states)
2. แทน เซตของสัญลักษณ์เข้าทั้งหมด (a set of input symbols)
3. q₀ แทน สถานะเริ่มต้น (the initial state)
4. F Q แทน เซตของสถานะยอมรับ (a set of accepting states)
5. : Q × Q แทน ฟังก์ชันการผ่าน (the transition function)

โดยทั่วไปเรา เขียนแทน DFA ด้วย 5 ลำดับคือ (Q, , , q₀, F)
ตัวอย่างที่ 1 กำหนดให้ Q = {q₀, q₁}, = {a, b}, F = {q₀} และ นิยามโดย

(q₀, a) = q₀, (q₀, b) = q₁, (q₁, a) = q₁, (q₁, b) = q₀

เราได้ว่า (Q, , , q₀, F) คือ DFA ซึ่งสำหรับฟังก์ชัน เราอาจนิยามโดยใช้ตารางแสดงการเปลี่ยนสถานะ

	a	b
q0	q0	q1
q1	q1	q0

เรายังใช้อีกวิธีหนึ่งในการกำหนด DFA โดยการใช้แผนภาพการผ่าน (Transition diagram)
นิยาม แผนภาพการผ่าน (Transition diagram) แสดงโดยใช้กราฟเทียมดังนี้

1. ทุกสถานะที่อยู่ใน Q เราเขียนแทนด้วยจุดยอดของกราฟ โดยมีลูกศรชี้เข้าที่สถานะเริ่มต้น (q₀)
2. สำหรับแต่ละสถานะที่อยู่ใน F เราเขียนจุดยอดในกราฟโดยมีวงกลมซ้อน เพื่อแสดงถึงสถานะยอมรับ
3. และสำหรับฟังก์ชันการผ่าน เราจะเขียนอาร์กที่มีทิศทางเชื่อมจากจุดยอด p ไปยังจุดยอด q โดยมี a เขียนกำกับ แทนจาก (p, a) = q

จากตัวอย่างที่ 1 เราจะได้แผนภาพการผ่านคือ

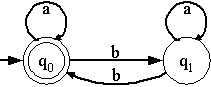
ข้อสังเกต ทุกจุดยอดมีจำนวนอาร์กที่ออกเท่ากับจำนวนสัญลักษณ์ที่ปรากฎใน
เราใช้ DFA สำหรับตอบคำถามต่าง ๆ ได้โดยใช้ การเดินในแผนภาพการผ่าน นั่นคือ เมื่อเรามีสายอักขระรับเข้าปรากฎใน แถบบันทึกรับเข้า เราทำการเดินโดย

1. เริ่มที่สถานะเริ่มต้น โดยกำหนดสถานะปัจจุบันให้เป็น q₀
2. ตั้งหัวอ่านชี้ไปที่ตัวอักขระตัวแรก
3. อ่านตัวอักขระจากแถบบันทึกรับเข้าหนึ่งตัว อ่านเสร็จแล้วขยับหัวอ่านไปทางขวา ในกรณีที่ตำแหน่งของหัวอ่านไม่มีตัวอักขระใดอยู่ให้หยุด แล้วไปที่ 5
4. เปลี่ยนสถานะปัจจุบันไปสถานะใหม่ โดยเลือกอาร์กที่มีตัวอักขระที่อ่านขึ้นมา แล้วย้อนกลับไปที่ 3
5. พิจารณาว่าสถานะปัจจุบันอยู่ใน F หรือไม่ ถ้าอยู่ให้ตอบยอมรับ มิฉะนั้นตอบไม่ยอมรับสายอักขระนั้น

เราจะยอมรับสายอักขระรับเข้า (สายอักขระที่ปรากฎบนแถบบันทึกรับเข้า) ก็ต่อเมื่อ สถานะสุดท้ายที่หยุดคือสถานะยอมรับ เราสามารถเขียนการทำงานนี้ให้อยู่ในรูปแบบเชิงคณิตศาสตร์ โดยใช้โครงแบบของ DFA
นิยาม โครงแบบ (Configuration) ของออโตมาตาจำกัดเชิงกำหนด
กำหนด M = (Q, , , q₀, F) เรากล่าวว่าคู่ลำดับ (q, w) Q × ^* เป็นโครงแบบหนึ่งของ M เมื่อในขณะนั้น M อยู่ในสถานะ q และหัวอ่านอยู่ที่สัญลักษณ์ตัวแรกสุดทางซ้ายของ w โดยปกติ w คือส่วนของข้อมูลบนแถบบันทึกรับเข้าที่ยังไม่ได้อ่าน เช่น (q₀, 0110100) เป็นโครงแบบหนึ่งของออโตมาตาจำกัดเชิงกำหนด ของรูปต่อไปนี้

เราเปลี่ยนโครงแบบได้โดยใช้กฎดังนี้

1. (p, x) (q, w) ก็ต่อเมื่อ x = aw, โดยที่ a , w ^* และ (p,a) = q
   หรือเขียนอีกแบบหนึ่งได้คือ (p, aw) (q, w) ก็ต่อเมื่อ a , w ^* และ (p,a) = q
2. (p, x) (q, w) ก็ต่อเมื่อ (p, x) = (q, w) หรือ มีคู่ลำดับ c₁, c₂, ..., c_n ที่ c₁ = (p, x), c₁ c₂, ..., c_n-1 c_n และ c_n = (q, w)

จากการนิยามสถานะยอมรับ ทำให้เราสรุปได้ว่าจะมีคำใน ^* บางคำซึ่งเครื่องออโตมาตาจำกัดเชิงกำหนดจะหยุดในสถานะยอมรับ และบางคำที่เครื่องออโตมาตาจำกัดเชิงกำหนดนี้จะหยุดในสถานะไม่ยอมรับ เราจะเรียกเซตของคำใน ^* ที่เครื่องออโตมาตาจำกัดเชิงกำหนดนี้ยอมรับว่า ภาษา (language) ที่เครื่องออโตมาตาจำกัดเชิงกำหนดยอมรับ
นิยาม เครื่องออโตมาตาจำกัดเชิงกำหนด M ยอมรับ w ก็ต่อเมื่อ

มี q F ที่ทำให้ (q₀, w) (q, )

และเราเรียกโครงแบบสุดท้ายนี้ว่า โครงแบบยอมรับ (accepting configuration)
เราเขียนแทน ภาษาที่ M ยอมรับ ด้วย L(M) คือ สับเซตของ ^* ที่ L(M) = { w ^* | M ยอมรับ w }
ตัวอย่าง 2 ให้ M = (Q, , , q₀, F) เป็นเครื่องออโตมาตาจำกัดเชิงกำหนดในตัวอย่างที่ 1

• จงตรวจสอบว่า M ยอมรับ aabba และ abbba หรือไม่
• จงแจงสมาชิกของ L(M) โดยเรียงจากสายอักขระที่มีขนาดเล็กไปขนาดใหญ่มาอย่างน้อย 10 ตัว
• จงอธิบายภาษา L ที่ได้ในรูปแบบเซตที่ใช้คำอธิบาย
• จงพิสูจน์ว่า L(M) = L

ตัวอย่าง 3 ของเด็กเล่นชิ้นหนึ่งประกอบด้วยจอภาพและแป้นพิมพ์ที่มีแป้นเพียง 2 แป้น โดยมีเลข 0 บนแป้นหนึ่ง และ 1 บนอีกแป้นหนึ่ง เมื่อเปิดจอภาพจะปรากฎรูปมังกรยืนนิ่ง ๆ

จอภาพมีรูปมังกรยืนนิ่ง กด 0 มังกรพ่นไฟ

จอภาพมีรูปมังกรยืนนิ่ง กด 1 มังกรพ่นน้ำ

จอภาพมีรูปมังกรพ่นไฟ กด 0 มังกรยืนนิ่ง

จอภาพมีรูปมังกรพ่นน้ำ กด 1 มังกรยืนนิ่ง

จอภาพมีรูปมังกรพ่นไฟ กด 1 มังกรพ่นน้ำ

จอภาพมีรูปมังกรพ่นน้ำ กด 0 มังกรพ่นไฟ

จงเขียนแผนภาพการผ่านของ DFA ที่เป็นตัวแบบของ ของเด็กเล่นชิ้นนี้ ถ้ากำหนดว่าสถานะยอมรับคือ สถานะที่จอภาพปรากฎรูปมังกรยืนนิ่ง
ตัวอย่าง 4 จงสร้าง DFA ที่ยอมรับเฉพาะสายอักขระ x {0, 1}^* ที่มี 0 ปรากฎอยู่เป็นจำนวนคู่ครั้งและ 1 ปรากฎอยู่เป็นจำนวนคี่ครั้ง

ออโตมาตาจำกัดเชิงไม่กำหนด (Nondeterministic Finite Automata)
เราพบว่าในการแก้ปัญหาบางครั้งเราอาจต้องการเลือกการเปลี่ยนสถานะไป q_i หรือ q_j ที่ต่างกัน เมื่ออ่านตัวอักขระตัวเดียวกันเราเรียกเครื่องออโตมาตาจำกัดที่มีความสามารถนี้ว่า ออโตมาตาจำกัดเชิงไม่กำหนด
นิยาม ออโตมาตาจำกัดเชิงไม่กำหนด (Nondeterministic Finite Automata or NFA)
ประกอบด้วย Q, , q₀ และ F เหมือนในออโตมาตาจำกัดเชิงกำหนด แต่ : Q × 2^Q
โดยที่ 2^Q หมายถึง เซตที่ประกอบด้วยสับเซตที่เป็นไปได้ทั้งหมดของ Q (Power set of Q) แต่ในกรณีนี้เราจะสนใจพิสัยที่เป็นเซตจำกัดเท่านั้น
เรามักเขียนแทนออโตมาตาจำกัดเชิงไม่กำหนดแต่ละเครื่องด้วย (Q, , , q₀, F)
หมายเหตุ NFA ต่างกับ DFA ตรงที่ฟังก์ชันการผ่านของออโตมาตาจำกัดเชิงไม่กำหนดมีค่าออกมาเป็นเซตของสถานะถัดไป ซึ่งทำให้เรามีทางเลือกในการเปลี่ยนสถานะ ไม่เหมือนออโตมาตาจำกัดเชิงกำหนดที่มีการเปลี่ยนสถานะที่มีทางเลือกเพียงทางเดียว
ในทำนองเดียวกับออโตมาตาจำกัดเชิงกำหนด เราสามารถเขียนแทนออโตมาตาจำกัดเชิงไม่กำหนดด้วย แผนภาพการผ่าน
นิยาม แผนภาพการผ่านของออโตมาตาจำกัดเชิงไม่กำหนด (Transition diagram for NFA)
แผนภาพการผ่านของออโตมาตาจำกัดเชิงไม่กำหนดคล้ายกับของออโตมาตาจำกัดเชิงกำหนด ยกเว้นข้อ (3) คือ

1. ทุกสถานะที่อยู่ใน Q เราเขียนแทนด้วยจุดยอดของกราฟเทียม โดยมีลูกศรชี้เข้าที่สถานะเริ่มต้น (q₀)
2. สำหรับแต่ละสถานะที่อยู่ใน F เราเขียนจุดยอดในกราฟโดยมีวงกลมซ้อน เพื่อแสดงถึงสถานะยอมรับ
3. และสำหรับฟังก์ชันการผ่าน เราจะเขียนอาร์กเชื่อมจากจุดยอด p ไปยังจุดยอด q โดยมี a เขียนกำกับ ก็ต่อเมื่อ q (p,a)

นิยาม โครงแบบ (Configuration) ของออโตมาตาจำกัดเชิงไม่กำหนด
โครงแบบของออโตมาตาจำกัดเชิงไม่กำหนดเหมือนของออโตมาตาจำกัดเชิงกำหนดโดยที่

1. (p, x) (q, w) ก็ต่อเมื่อ x = aw, โดยที่ a , w ^* และ q (p,a) นั่นคือ โครงแบบถัดจาก (p, x) อาจมีมากกว่า 1 โครงแบบ
2. (p, x) (q, w) ก็ต่อเมื่อ (p, x) = (q, w) หรือ มีคู่ลำดับ c₁, c₂, . . ., c_n ที่

   c₁ = (p, x), c₁ c₂, ..., c_n-1 c_n และ c_n = (q, w)

นิยาม ออโตมาตาจำกัดเชิงไม่กำหนด M ยอมรับ w ก็ต่อเมื่อ มี q F ที่ทำให้ (q₀, w) (q, )
ภาษาที่ M ยอมรับ เขียนแทนด้วย L(M) = { w ^* | M ยอมรับ w } ในกรณีที่ (p,a) = Ø เราจะถือว่าสายอักขระนั้นทั้งสายไม่ยอมรับโดยเครื่องออโตมาตานี้
ตัวอย่าง 5 ให้ M = (Q, , , q₀, F) เป็น NFA ที่มี Q = {q₀, q₁, q₂ }, = {a, b}, F = {q₀} และ นิยามดังนี้

(q₀,a)={q₀,q₂}, (q₀,b)={q₁, q₂}, (q₁,a)={q₂}, (q₁,b)={q₀}, (q₂,a)=Ø , (q₂,b)={q₁}

เขียนเป็นตารางได้ดังนี้

	a	b
q0	{ q0, q2 }	{ q1, q2 }
q1	{q2}	{q0}
q2	Ø	{q1}

• จงเขียนแผนภาพการผ่านของ M
• จงตรวจสอบว่า M ยอมรับ aabba และ aab หรือไม่
• จงแจงสมาชิกของ L(M) โดยเรียงจากสายอักขระที่มีขนาดเล็กไปขนาดใหญ่มาอย่างน้อย 10 ตัว

จากการทดสอบสมาชิก โดยการเขียนโครงแบบทำให้เราทราบว่า เราสามารถกำหนดฟังก์ชัน อีกลักษณะหนึ่งซึ่งเกิดจากฟังก์ชัน ได้โดยที่ฟังก์ชันนี้จะให้ค่าเดียวกับฟังก์ชัน ถ้าเราพิจารณาตัวอักขระทีละตัว แต่ถ้าเราสนใจสายอักขระที่มากกว่าหนึ่งตัว เราจะได้ฟังก์ชันใหม่ที่นิยามดังนี้
นิยาม การขยาย ไปสู่ ที่มีโดเมนเป็น Q × ^*
ให้ M = (Q, , , q₀, F) เป็น NFA เรานิยาม : Q × ^* 2^Q ดังนี้

1. สำหรับแต่ละ q Q ให้ (q, ) = {q} (นิยามที่ 1 ของ )
2. สำหรับแต่ละ q Q แต่ละ w ^* แต่ละ a
   ถ้า (q, w) = {p₁, p₂, . . ., p_n} แล้ว (นิยามที่ 2 ของ )

   (q, wa) = (p₁, a) (p₂, a) ... (p_n, a) = (p_i, a)

ข้อสังเกต (q, ) = {q}, (q, a) = (q, a) และ ถ้า S Q เรานิยาม (S, w) = (q, w)
เราสามารถทดสอบการยอมรับสายอักขระได้อีกวิธีคือ M ยอมรับ w ก็ต่อเมื่อ (q₀, w) F Ø
ทฤษฎีบท สำหรับทุก w ^*, q (q₀, w) ก็ต่อเมื่อ (q₀, w) (q, )
พิสูจน์

ให้ P(n) แทนข้อความ w ^* ซึ่ง |w| = n, q (q₀, w) ก็ต่อเมื่อ (q₀, w) (q, )

เราจะแสดงโดยใช้อุปนัยเข้มบนความยาวของ w ว่า P(n) เป็นจริงทุก n = |w| ที่เป็นจำนวนนับรวมศูนย์

มูลฐานของการอุปนัย ให้ w ^* โดยที่ |w| = 0 ดังนั้น w =

q (q0, ) = {q0}	ได้ว่า	q = q0
		(q0, w) = (q0, ) = (q, ) ดังนั้น (q0, w) (q, )

(q0, w) (q, )	ได้ว่า	q = q0 เพราะ w =
		(q0, ) = {q0}
		q = q0 (q0, )

ดังนั้น P(0) เป็นจริง
ขั้นอุปนัย เราเริ่มจากสมมติฐานของการอุปนัย
สมมติว่า P(k) เป็นจริง ดังนั้นทุก w ^* โดยที่ |w|=k, q (q₀, w) ก็ต่อเมื่อ (q₀,w) (q,)
เราต้องการแสดงว่า P(k + 1) เป็นจริงนั่นคือทุก wa ^* โดยที่ | wa | = k+1, q (q₀, wa) ก็ต่อเมื่อ (q₀, wa) (q, )

q(q0, wa)	จากนิยามที่ 2 ได้ว่า	มี p Q ซึ่ง q (p, a) และ p (q0, w)
		p Q และ q (p, a) และ (q0, w) (p, ) โดยสมมติฐานการอุปนัย
		(q0,wa) (p,a)(p,a) (q,) โดยนิยาม และ q(p,a)

(q0, wa) (q, )	จะได้ว่า	(q0, wa) (p, a) (q, ) สำหรับบาง p Q
		(q0, w) (p, ) และ (p, a) = q
		p (q0, w) และ (p, a) = q
		q (q0, wa)

ดังนั้น P(k + 1) เป็นจริง

จบการพิสูจน์

จากทฤษฎีดังกล่าวทำให้เราได้ว่า M ยอมรับ w ก็ต่อเมื่อ มี q F ซึ่ง (q₀, w) (q, ) ก็ต่อเมื่อ มี q F และ q (q₀, w) ก็ต่อเมื่อ (q₀, w) F Ø
ตัวอย่าง 6 กำหนดออโตมาตาจำกัดเชิงไม่กำหนด M ให้ดังรูป

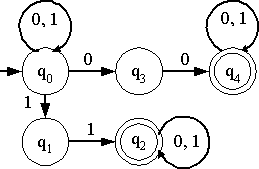
• จงตรวจสอบว่า M ยอมรับ 01001 และ 01010 หรือไม่
• จงแจงสมาชิกของ L(M) โดยเรียงจากสายอักขระที่มีขนาดเล็กไปขนาดใหญ่มาอย่างน้อย 10 ตัว
• จงอธิบายภาษา L ที่ได้ในรูปแบบเซตที่ใช้คำอธิบาย
• จงพิสูจน์ว่า L(M) = L

ตัวอย่าง 7 วิศวกรผู้หนึ่งสร้างหุ่นยนต์ที่มีสองมือไว้สำหรับจัดชุดถ้วยกาแฟในโรงอาหาร โดยหุ่นยนต์จะหยิบถ้วยหรือจานรอง ซึ่งส่งผ่านมาทางสายพานเรียงแถวทีละหนึ่งชิ้น โดยมีหลักการทำงานดังนี้

1. ถ้ามือของหุ่นยนต์ว่างทั้งสองมือ หุ่นยนต์จะเริ่มหยิบภาชนะด้วยมือซ้าย (ภาชนะนั้นอาจจะเป็นถ้วยหรือจานรองก็ได้)
2. ถ้ามือซ้ายถือภาชนะชิ้นหนึ่งอยู่ มือขวาจะหยิบภาชนะคนละชนิดกับที่ถืออยู่ในมือซ้าย
3. หุ่นยนต์จะต้องเอาถ้วยวางบนจานรอง และส่งออกทางสายพานอีกอันหนึ่ง
4. เมื่อหมดแถวของภาชนะที่ส่งผ่านมาให้จัดชุดแล้ว มือทั้งสองของหุ่นยนต์ต้องไม่ถือภาชนะใดเลย

จงเขียนแผนภาพแสดงการผ่านของออโตมาตาจำกัดเชิงไม่กำหนด M ที่เป็นตัวแบบของหุ่นยนต์ตัวนี้ โดยระบุให้ชัดเจนว่า สถานะเริ่มต้น และสถานะอื่นๆ ที่เกี่ยวข้องกับหุ่นยนต์ตัวนี้คืออะไร กำหนดว่าสถานะยอมรับคือสถานะที่มือทั้งสองของหุ่นยนต์ต้องไม่ถือภาชนะใดเลย
ตัวอย่าง 8 จงสร้างออโตมาตาจำกัดเชิงไม่กำหนด M ที่ยอมรับภาษา {x {0,1}^* | x ไม่มีเลข 0 เขียนเรียงติดกัน 3 ตัว }
นอกจากนี้ เราอาจต้องการเขียนออโตมาตาจำกัดที่สามารถเปลี่ยนสถานะได้โดยไม่จำเป็นต้องอ่านตัวอักขระในแถบบันทึกรับเข้า วิธีการคือเรากำหนดสัญลักษณ์พิเศษเรียกว่าอักขระว่าง ()
นิยาม NFA w/-moves
NFA w/-moves ประกอบด้วย Q, , F, q₀ เหมือนของออโตมาตาจำกัดเชิงไม่กำหนด แต่ฟังก์ชันการผ่าน จะรวมการพิจารณาตัวอักขระว่างด้วย กล่าวคือ 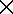: Q ( {}) 2^Q
นิยาม แผนภาพการผ่านของออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้ายโดย-
ให้ M = (Q, , , q₀, F) เป็นออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้ายโดย- แผนภาพการผ่านของออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้ายโดย- คือกราฟเทียมที่

1. มี Q เป็นเซตของจุดยอดทั้งหมด และมีลูกศรชี้เข้าที่ q₀
2. มีวงกลม 2 วงล้อมรอบจุดยอดทุกจุดใน F และ
3. จะมีอาร์กเชื่อมจาก p ไป q โดยมี a {} เขียนกำกับ ก็ต่อเมื่อ q (p, a)

ตัวอย่าง 9 ของเด็กเล่นชิ้นหนึ่งประกอบด้วยจอภาพและแป้นพิมพ์ ซึ่งมีสัญลักษณ์ + - × = ? 0 1 2 3 4 5 6 7 8 9 ปรากฎแป้นละหนึ่งตัว ของเด็กเล่นชิ้นนี้สอนรูปแบบที่ถูกต้องของการบวก ลบ คูณ จำนวนเต็มที่ไม่เป็นลบดังนี้

1. จำนวนเต็มตั้งแต่สองหลักขึ้นไป ไม่เริ่มต้นด้วย 0
2. + - × เขียนติดกันไม่ได้
3. สายอักขระต้องเริ่มด้วยจำนวนเต็มเท่านั้น
4. = ต้องอยู่ระหว่าง จำนวนเต็มกับ ? เท่านั้น
5. ถ้ามี + - × ปรากฎอย่างน้อย 1 ครั้ง สายอักขระนั้นต้องลงท้ายด้วย =? และ =? ปรากฎเพียงครั้งเดียว
6. ถ้าไม่มี + - × ปรากฎต้องไม่มี =? ปรากฎด้วย

บนจอภาพมี ปุ่มเฉลย ซึ่งเมื่อพิมพ์เสร็จให้กดปุ่มนี้ ถ้าสายอักขระที่เด็กพิมพ์อยู่ในรูปที่ถูกต้องของเด็กเล่นชิ้นนี้จะส่งเสียงว่าถูกต้อง มิฉะนั้นของเล่นชิ้นนี้จะส่งเสียงว่าไม่ถูกต้อง

จงเขียนแผนภาพการผ่านของออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้ายโดย- ที่เป็นตัวแบบของเด็กเล่นชิ้นนี้

เราจะทำการขยายฟังก์ชัน ไปยัง โดยใช้หลักการเดียวกัน แต่เราต้องนิยามสมบัติบางอย่างเพื่อนำไปใช้ก่อน
นิยาม (Epsilon closure) : สำหรับแต่ละสถานะ q Q ใด ๆ เรากำหนด

-CL(q) = {q} { p Q | มีวิถีจาก q ไปยัง p โดยที่ทุกอาร์กในวิถีนั้นมี เขียนกำกับ }

และสำหรับ S Q ใด ๆ

-CL(S) = -CL(q)

นิยาม การขยายฟังก์ชัน ไปสู่
ให้ M = (Q, , , q₀, F) เป็นออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้ายโดย- กำหนด : Q ^* 2^Q โดยที่

1. สำหรับแต่ละ q Q ให้ (q, ) = -CL(q)
2. สำหรับแต่ละ q Q, w ^*, a , ถ้า (q, w) = {p₁, p₂, p₃, . . . , p_n} แล้ว (q, wa) = -CL(S) เมื่อ S = (p, a)

เราสามารถทดสอบการยอมรับของสายอักขระได้คล้ายกับเครื่องออโตมาตาจำกัดเชิงไม่กำหนด กล่าวคือ M ยอมรับ w ก็ต่อเมื่อ (q₀, w) F
ภาษาที่ M ยอมรับ เขียนแทนด้วย L(M) = { w ^* | M ยอมรับ w }
ทฤษฎีบท สำหรับทุก w ^*, q (q₀, w) ก็ต่อเมื่อ (q₀, w) (q, )
การพิสูจน์ใช้หลักการเดียวกับการพิสูจน์ของเครื่องออโตมาตาจำกัดเชิงไม่กำหนด แต่จะมีรายละเอียดที่ต้องพิจารณามากกว่า
ตัวอย่าง 10

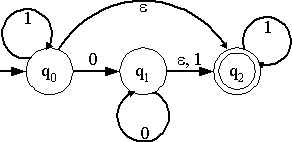
• จงหา -CL(q₀)
• (q₀, 10) และ (q₀, 01)
• จงตรวจสอบว่า M ยอมรับ 10 และ 01 หรือไม่
• จงแจงสมาชิกของ L(M) โดยเรียงจากสายอักขระที่มีขนาดเล็กไปขนาดใหญ่มาอย่างน้อย 10 ตัว
• จงอธิบายภาษา L ที่ได้ในรูปแบบเซตที่ใช้คำอธิบาย
• จงพิสูจน์ว่า L(M) = L

ตัวอย่าง 11 จงสร้างออโตมาตาจำกัดเชิงไม่กำหนด M ที่มีการย้ายโดย- โดย L(M) = { x {0, 1}^* | มี n ₀, x = (01)ⁿ0 }