ปัญหาที่ตัดสินได้และตัดสินไม่ได้ (Decidable and undecidable problems)
จากการสร้างเครื่องออโตมาตาและเครื่องทัวริงที่ผ่านมา เราพบว่าเครื่องทัวริงมีความสามารถในการจดจำเซต รูปแบบ
คำนวณค่าฟังก์ชัน และจำลองการทำงานหรือขั้นตอนวิธีของการคำนวณต่าง ๆ ได้ เราจึงเลือกสถาปัตยกรรมเครื่องทัวริงในการใช้ในการตอบคำถามที่ว่า
"มีขั้นตอนวิธีที่จะตรวจสอบข้อความที่กำหนดให้หรือไม่" ตัวอย่างของคำถามเช่น
- "มีขั้นตอนวิธีที่ใช้ตรวจสอบว่าโปรแกรมใด ๆ หยุดการทำงานเสมอสำหรับทุกสายอักขระ หรือไม่"
- "มีขั้นตอนวิธีที่ใช้ตรวจสอบว่ากราฟที่มีทิศทางใด ๆ มีวงแฮมิลตัน หรือไม่"
- "มีขั้นตอนวิธีที่ใช้ตรวจสอบว่าภาษาที่ได้จากโปรแกรมที่พิจารณา เป็นภาษาซึ่งไม่มีสมาชิกอยู่เลย หรือไม่"
บทนิยาม : ปัญหาที่อยู่ในรูปแบบคำถามว่า "มีหรือไม่มี ขั้นตอนวิธีที่จะใช้ตรวจสอบข้อความที่กำหนดให้" เป็น
ปัญหาที่ตัดสินได้ (decidable problem) ก็ต่อเมื่อ ภาษาที่มีความหมายตรงกับข้อความในปัญหานั้นเป็นเซตรีเคอร์ซีฟ
และเรากล่าวว่า ปัญหานั้นเป็น ปัญหาที่ตัดสินไม่ได้ (undecidable problem) ก็ต่อเมื่อ ภาษาที่มีความหมายตรงกับข้อความในปัญหานั้น
ไม่เป็นเซตรีเคอร์ซีฟ
ตัวอย่างที่ 1: ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่ใช้ตรวจสอบว่า สำหรับเครื่องทัวริง M ใด ๆ และสายอักขระ w, M ยอมรับ w หรือไม่"
เป็นปัญหาที่ตัดสินไม่ได้ เพราะภาษาที่ได้มีความหมายเดียวกับ Lu ซึ่งไม่เป็นเซตรีเคอร์ซีฟ
ตัวอย่างที่ 2: ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่ใช้ตรวจสอบว่า สำหรับไวยากรณ์ไม่พึ่งบริบท G ใด ๆ L(G) = Ø หรือไม่"
เป็นปัญหาที่ตัดสินได้ เพราะเราสามารถเขียนขั้นตอนวิธีในการตรวจสอบว่า ไวยากรณ์ไม่พึ่งบริบทผลิตสายอักขระใด ๆ หรือไม่
การพิสูจน์ว่าปัญหาที่ตัดสินได้สามารถทำได้โดยอธิบายการสร้างเครื่องทัวริงก็เพียงพอ แต่สำหรับการแสดงว่า
ปัญหาที่พิจารณาเป็นปัญหาที่ตัดสินไม่ได้จะมีความยุ่งยากกว่า เราจึงเสนอวิธีการที่ง่ายขึ้นโดยใช้ทฤษฎีบทของไรซ์
ทฤษฎีบทของไรซ์ : (Rice's Theorem) ให้ 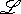
 {L | L เป็นเซตอาร์อี} จะได้ว่า {<M> | M เป็นเครื่องทัวริง และ L(M) {L | L เป็นเซตอาร์อี} จะได้ว่า {<M> | M เป็นเครื่องทัวริง และ L(M)
 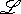 } เป็นเซตรีเคอร์ซีฟ ก็ต่อเมื่อ } เป็นเซตรีเคอร์ซีฟ ก็ต่อเมื่อ
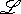 = Ø หรือ = Ø หรือ 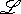 = {L |
L เป็นเซตอาร์อี} = {L |
L เป็นเซตอาร์อี}
สังเกตว่า 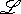 เป็นเซตซึ่งประกอบด้วยภาษา ดังนั้นการใช้ทฤษฎีบทของไรซ์ เราเริ่มจากการนิยาม เป็นเซตซึ่งประกอบด้วยภาษา ดังนั้นการใช้ทฤษฎีบทของไรซ์ เราเริ่มจากการนิยาม
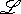 ที่เป็นเซตของภาษา ถ้าเราต้องการแสดงว่า
{<M> | M เป็นเครื่องทัวริง และ L(M) ที่เป็นเซตของภาษา ถ้าเราต้องการแสดงว่า
{<M> | M เป็นเครื่องทัวริง และ L(M)  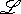 }
ไม่เป็นเซตรีเคอร์ซีฟ เราเพียงหา L1 }
ไม่เป็นเซตรีเคอร์ซีฟ เราเพียงหา L1 
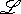 และ L1 และ L1  {L | L เป็นเซตอาร์อี}
{L | L เป็นเซตอาร์อี}  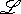 C C
ตัวอย่างที่ 3: ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่ใช้ตรวจสอบว่า สำหรับเครื่องทัวริง M ใด ๆ M หยุดการทำงานเสมอ
เมื่ออ่านสายอักขระรับเข้าใด ๆ หรือไม่" เป็นปัญหาที่ตัดสินได้หรือไม่ได้
ตัวอย่างที่ 4: ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่ใช้ตรวจสอบว่า สำหรับเครื่องทัวริง M ใด ๆ L(M) = Ø หรือไม่"
เป็นปัญหาที่ตัดสินได้หรือไม่ได้
ตัวอย่างที่ 5: ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่ใช้ตรวจสอบว่า สำหรับเครื่องทัวริง M ใด ๆ L(M) เป็นเซตจำกัด หรือไม่"
เป็นปัญหาที่ตัดสินได้หรือไม่ได้
ตัวอย่างที่ 6: ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่ใช้ตรวจสอบว่า สำหรับเครื่องทัวริง M ใด ๆ L(M) เป็นเซตรีเคอร์ซีฟ หรือไม่"
เป็นปัญหาที่ตัดสินได้หรือไม่ได้
ตัวอย่างที่ 7: ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่ใช้ตรวจสอบว่า สำหรับเครื่องทัวริง M ใด ๆ M หยุดการทำงานเสมอ
เมื่ออ่านสายอักขระรับเข้าใด ๆ หรือไม่" เป็นปัญหาที่ตัดสินได้หรือไม่ได้
จากปัญหาที่กล่าวข้างต้น เราสนใจเฉพาะปัญหาที่เกี่ยวข้องกับเครื่องทัวริงทั้งสิ้น แต่ปัญหาที่ตัดสินไม่ได้บางปัญหาอาจไม่เกี่ยวข้องกับ
การสร้างเครื่องทัวริงเลยก็ได้ เช่น ปัญหาการสมนัยของโพสต์ (Post's correspondence problem) ซึ่งสามารถนำไปใช้พิสูจน์ ว่าปัญหาอื่น ๆ
เป็นปัญหาที่ตัดสินไม่ได้
บทนิยาม : ให้ A และ B เป็นรายการ (list) ของสายอักขระใน
 + ที่มีจำนวนสายอักขระเท่ากัน
เราจะนิยาม คู่กรณีของพีซีพี (A, B) ว่าเป็น คู่กรณีของปัญหาการสมนัยของโพสต์ (instance of Post's correspondence problem) ดังนี้ + ที่มีจำนวนสายอักขระเท่ากัน
เราจะนิยาม คู่กรณีของพีซีพี (A, B) ว่าเป็น คู่กรณีของปัญหาการสมนัยของโพสต์ (instance of Post's correspondence problem) ดังนี้
สมมติว่า (A, B) เป็นคู่กรณีของพีซีพี โดยที่
- A เป็นรายการของสายอักขระ w1, w2, ..., wk
- B เป็นรายการของสายอักขระ x1, x2, ..., xk
เรากล่าวว่าคู่กรณีของพีซีพี (A, B) มีผลเฉลย (solution) ก็ต่อเมื่อ เราสามารถหาลำดับของจำนวนเต็ม i1, i2, ..., im ได้ โดยที่
wi1wi2...wim = xi1xi2...xim
เราเรียก i1, i2, ..., im ว่าเป็นผลเฉลยของคู่กรณีของพีซีพี (A, B) และเรากล่าวว่า wi1wi2...wim =
xi1xi2...xim เป็น รูปแบบที่เข้าชุดกัน (match) ของคู่กรณีของพีซีพี (A, B)
บทนิยาม : ปัญหาการสมนัยของโพสต์ (Post's correspondence problem) เขียนสั้น ๆ ว่า พีซีพี
(PCP) คือปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่ใช้ตรวจสอบว่า คู่กรณีของพีซีพี (A, B) คู่ใด ๆ มีผลเฉลยหรือไม่"
ตัวอย่างที่ 8: ให้  = {0, 1} และ A, B เป็นรายการของสายอักขระ
w1, w2, w3 และ x1, x2, x3 ตามลำดับ โดยที่
w1 = 1, w2 = 10111, w3 = 10 และ x1 = 111, x2 = 10, x3 = 0
จงหาผลเฉลยของ (A, B) ถ้ามี = {0, 1} และ A, B เป็นรายการของสายอักขระ
w1, w2, w3 และ x1, x2, x3 ตามลำดับ โดยที่
w1 = 1, w2 = 10111, w3 = 10 และ x1 = 111, x2 = 10, x3 = 0
จงหาผลเฉลยของ (A, B) ถ้ามี
ตัวอย่างที่ 9: ให้  = {0, 1} และ A, B เป็นรายการของสายอักขระ
w1, w2, w3 และ x1, x2, x3 ตามลำดับ โดยที่
w1 = 10, w2 = 011, w3 = 101 และ x1 = 101, x2 = 11, x3 = 011
จงหาผลเฉลยของ (A, B) ถ้ามี = {0, 1} และ A, B เป็นรายการของสายอักขระ
w1, w2, w3 และ x1, x2, x3 ตามลำดับ โดยที่
w1 = 10, w2 = 011, w3 = 101 และ x1 = 101, x2 = 11, x3 = 011
จงหาผลเฉลยของ (A, B) ถ้ามี
บทนิยาม : ปัญหาการสมนัยของโพสต์ปรับปรุง (Modified Post's correspondence problem) หรือ
เขียนสั้น ๆ ว่า เอ็มพีซีพี (MPCP) คือปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่จะตรวจสอบว่าคู่กรณีของพีซีพี (A, B) คู่ใด ๆ มีผลเฉลย
i1, i2, ..., im หรือไม่ โดยที่ i1 = 1"
ทฤษฎีบท : ถ้า พีซีพี เป็นปัญหาที่ตัดสินได้แล้ว เอ็มพีซีพี จะเป็นปัญหาที่ตัดสินได้ด้วย
พิสูจน์
สมมติว่า พีซีพี เป็นปัญหาที่ตัดสินได้ ดังนั้นจะมีขั้นตอนวิธีที่จะตรวจสอบว่า คู่กรณีของพีซีพี (A, B) คู่ใด ๆ มีผลเฉลยหรือไม่ เรียกขั้นตอนวิธีดังกล่าวว่า S
(เราจะแสดงการสร้างขั้นตอนวิธีสำหรับ เอ็มพีซีพี โดยการเพิ่มสัญลักษณ์ ฿ และ $)
ให้ (A, B) เป็นคู่กรณีของเอ็มพีซีพีคู่ใด ๆ A ประกอบด้วย w1, ..., wk และ B ประกอบด้วย x1, ..., xk
เราสร้างคู่กรณีของพีซีพี (A', B') จากชุดของ (A, B) ซึ่ง (A, B) มีผลเฉลย i1, i2, ..., im โดยที่ i1 = 1 ก็ต่อเมื่อ (A', B') มีผลเฉลย ดังนี้
ให้ ฿ และ $ เป็นสัญลักษณ์ที่ไม่ปรากฎใน  สำหรับแต่ละ i สำหรับแต่ละ i
- ให้ yi เป็นสายอักขระที่ได้จาก wi โดยการเติม ฿ ต่อท้ายสัญลักษณ์ทุกตัวที่ปรากฎใน wi
- ให้ zi เป็นสายอักขระที่ได้จาก xi โดยการเติม ฿ นำหน้าสัญลักษณ์ทุกตัวที่ปรากฎใน xi
ตัวอย่างเช่น ถ้า w1 = 0111 จะได้ y1 = 0฿1฿1฿1฿ และถ้า x1 = 110 จะได้ z1 = ฿1฿1฿0
และ y0 = ฿y1, z0 = z1, yk+1 = $ และ zk+1 = ฿$
ให้ลำดับของ y0, ..., yk+1 เป็นรายการของสายอักขระใน A' และ ลำดับของ
z0, ..., zk+1 เป็นรายการของสายอักขระใน B' ตามลำดับ
เราได้ว่า ถ้า i1, i2, ..., im เป็นผลเฉลยของคู่กรณีของเอ็มพีซีพี (A, B) โดยที่ i1 = 1 แล้วจะได้ว่า 0, i2, ..., im, k+1 เป็นผลเฉลยของคู่กรณี พีซีพี (A', B')
ทฤษฎีบท : เอ็มพีซีพี เป็นปัญหาที่ตัดสินไม่ได้
พิสูจน์ โดยใช้วิธีขัดแย้ง สมมติว่า เอ็มพีซีพีเป็นปัญหาที่ตัดสินได้ ดังนั้นจะมีขั้นตอนวิธีที่จะตรวจสอบว่า คู่กรณีของพีซีพี คู่ใด ๆ มีผลเฉลย
i1, i2, ..., im หรือไม่โดยที่ i1 = 1 เรียกขั้นตอนวิธีนี้ว่า S
(เราสามารถแสดงว่า มีขั้นตอนวิธีที่ตรวจสอบว่า สำหรับเครื่องทัวริง M ใด ๆ และสำหรับ w
  * ใด ๆ M ยอมรับ w หรือไม่) * ใด ๆ M ยอมรับ w หรือไม่)
ให้ M เป็นเครื่องทัวริงและ w   *
เราสร้างคู่กรณีของพีซีพี (A, B) จาก < M, w > โดยมีสมบัติว่า M ยอมรับ w ก็ต่อเมื่อ (A, B) มีผลเฉลย i1, i2, ..., im ที่ i1 = 1 ดังนี้ *
เราสร้างคู่กรณีของพีซีพี (A, B) จาก < M, w > โดยมีสมบัติว่า M ยอมรับ w ก็ต่อเมื่อ (A, B) มีผลเฉลย i1, i2, ..., im ที่ i1 = 1 ดังนี้
เราสมมติโดยไม่เสียนัยได้ว่า q1 เป็นสถานะเริ่มต้นของเครื่อง M และหัวอ่านเคลื่อนซ้ายหรือขวาเท่านั้น
สมาชิกของรายการ A และรายการ B เขียนแจกแจงเป็นกลุ่ม ๆ ดังนี้
| รายการ A |
รายการ B |
|
|---|
| คู่แรก | # |
#q1Z0w# |
|
| กลุ่ม I |
X |
Y |
X in {0, 1,  , Z0} , Z0} |
| กลุ่ม II |
qX |
Yp |
ถ้า  (q, X) = (p, Y, R) (q, X) = (p, Y, R) |
| กลุ่ม II |
ZqX |
pZY |
ถ้า  (q, X) = (p, Y, L) (q, X) = (p, Y, L) |
| กลุ่ม II |
q# |
Yp# |
ถ้า  (q, (q,  ) = (p, Y, R) ) = (p, Y, R) |
| กลุ่ม II |
Zq# |
pZY# |
ถ้า  (q, (q,  ) = (p, Y, L) ) = (p, Y, L) |
| กลุ่ม III |
XqY |
q |
สำหรับ q  F F |
| กลุ่ม III |
Xq |
q |
สำหรับ q  F F |
| กลุ่ม III |
qY |
q |
สำหรับ q  F F |
| กลุ่ม IV |
q#Z0# |
# |
ทุก q  F F |
เราสามารถแสดงได้ว่า คู่กรณี (A, B) ที่สร้างขึ้นมาจาก < M, w > มีผลเฉลย i1, i2, ..., im โดยที่ i1 = 1 ก็ต่อเมื่อ M ยอมรับ w
ปัญหาที่ถามว่า "มีหรือไม่มี ขั้นตอนวิธีที่จะตรวจสอบว่า สำหรับเครื่องทัวริง M ใด ๆ และสำหรับ
w   *
M ยอมรับ w หรือไม่" สามารถตรวจสอบได้ดังนี้ *
M ยอมรับ w หรือไม่" สามารถตรวจสอบได้ดังนี้
- สร้างคู่กรณี (A, B) ข้างต้น
- เนื่องจากเอ็มพีซีพี เป็นปัญหาที่ตัดสินได้ โดยมีขั้นตอนวิธี S เราใช้ขั้นตอนวิธี S ในการหาผลเฉลย
- จากผลเฉลยที่ได้ นำไปตอบปัญหาว่า M ยอมรับ w ได้
สรุปได้ว่า "มีหรือไม่มีขั้นตอนวิธีที่จะตรวจสอบว่า สำหรับเครื่องทัวริง M ใด ๆ และสำหรับ w 
 * M ยอมรับ w หรือไม่" เป็นปัญหาที่ตัดสินได้ ซึ่งขัดแย้ง * M ยอมรับ w หรือไม่" เป็นปัญหาที่ตัดสินได้ ซึ่งขัดแย้ง
ดังนั้น เอ็มพีซีพี เป็นปัญหาที่ตัดสินไม่ได้
บทแทรก : พีซีพี เป็นปัญหาที่ตัดสินไม่ได้
ตัวอย่างที่ 10: ให้ M = ({q1, q2, q3, q4}, {0,1}, {0, 1,
 , Z0}, , Z0},  , q1,
Z0, {q2}) เป็นเครื่องทัวริงแถบเดียวปลายเปิดทางเดียวที่มีนิยาม , q1,
Z0, {q2}) เป็นเครื่องทัวริงแถบเดียวปลายเปิดทางเดียวที่มีนิยาม
 ดังนี้ ดังนี้
-
 (q1, Z0) = (q1, Z0, R), (q1, Z0) = (q1, Z0, R),
 (q1, 1) = (q1, 1, R), (q1, 1) = (q1, 1, R),
 (q1, 0) = (q3, 0, R), (q1, 0) = (q3, 0, R),
 (q1, (q1,  ) = (q2, ) = (q2,
 , R), , R),  (q3, 1) = (q3,
1, R), (q3, 1) = (q3,
1, R),  (q3, 0) = (q4, 0, L), (q3, 0) = (q4, 0, L),
 (q4, 1) = (q4, 1, L), (q4, 1) = (q4, 1, L),
 (q4, 0) = (q2, 1, R) (q4, 0) = (q2, 1, R)
จงสร้างคู่กรณีของพีซีพี (A, B) จาก <M, 010> ตามขั้นตอนวิธีการพิสูจน์ข้างต้น และหาผลเฉลยของคู่กรณีที่ได้ ถ้ามี
ทฤษฎีบท : ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่จะตรวจสอบว่า ไวยากรณ์ไม่พึ่งบริบท G กำกวมหรือไม่"
เป็นปัญหาที่ตัดสินไม่ได้
พิสูจน์ โดยใช้วิธีขัดแย้ง สมมติว่า ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่จะตรวจสอบว่า ไวยากรณ์ไม่พึ่งบริบท G กำกวมหรือไม่"
เป็นปัญหาที่ตัดสินได้ ดังนั้นจะมีขั้นตอนวิธีที่จะตรวจสอบว่า ไวยากรณ์ไม่พึ่งบริบท G กำกวมหรือไม่ เรียกขั้นตอนวิธีนี้ว่า K
(เราสามารถแสดงว่า มีขั้นตอนวิธีที่ตรวจสอบว่า คู่กรณีของพีซีพี (A, B) คู่ใด ๆ มีผลเฉลยหรือไม่)
ให้ (A, B) เป็นคู่กรณีของพีซีพีคู่ใด ๆ เราสร้าง ไวยากรณ์ไม่พึ่งบริบทจาก (A, B) โดยให้มีสมบัติว่า G กำกวม ก็ต่อเมื่อ (A, B) มีผลเฉลย ดังนี้
กำหนดให้รายการ A ประกอบด้วย w1, ..., wk และ รายการ B ประกอบด้วย x1, ..., xk
โดยที่ wi, xi   +
ทุก i = 1, 2, ..., k +
ทุก i = 1, 2, ..., k
เลือก a1, ..., ak ที่ไม่ปรากฎใน  และสร้างเซต LA และ LB ดังนี้ และสร้างเซต LA และ LB ดังนี้
- LA = { wi1...wimaim...ai1 | m

 , i1, i2, ..., im , i1, i2, ..., im  {1, 2, ..., n} } {1, 2, ..., n} }
- LB = { xi1...ximaim...ai1 | m

 , i1, i2, ..., im , i1, i2, ..., im  {1, 2, ..., n} } {1, 2, ..., n} }
สร้างไวยากรณ์ G = < {S, SA, SB},   {a1, ..., ak}, P, S > ที่มีเซตของการผลิต P = {
{a1, ..., ak}, P, S > ที่มีเซตของการผลิต P = {
- S
 SA | SB SA | SB
- SA
 wiSAai | wiai ทุก i = 1, 2, ..., n wiSAai | wiai ทุก i = 1, 2, ..., n
- SB
 xiSBai | xiai ทุก i = 1, 2, ..., n xiSBai | xiai ทุก i = 1, 2, ..., n
}
เราพบว่า G กำกวม โดยที่ L(G) = LA  LB ก็ต่อเมื่อ คู่กรณี (A, B) มีผลเฉลย LB ก็ต่อเมื่อ คู่กรณี (A, B) มีผลเฉลย
เราสามารถแสดงได้ว่าปัญหาพีซีพี เป็นปัญหาที่ตัดสินได้ดังนี้
- จากคู่กรณี (A, B) ข้างต้น เราสร้างไวยากรณ์ G
- เนื่องจากปัญหาการทดสอบว่าไวยากรณ์กำกวมหรือไม่เป็นปัญหาที่ตัดสินได้ โดยมีขั้นตอนวิธี K เราใช้ขั้นตอนวิธี K ในการหาคำที่ผลิตออกมาจากต้นไม้ที่ต่างกันสองต้น
ซึ่งต้องได้มาจาก LA และ LB
- จากคำตอบที่ได้ทำให้เราสามารถหาผลเฉลยของคู่กรณี (A, B) โดยดูจาก ai1, ..., aim ที่ได้
สรุปได้ว่า ปัญหาพีซีพีเป็นปัญหาที่ตัดสินได้ ซึ่งขัดแย้ง
ดังนั้น ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่จะตรวจสอบว่า ไวยากรณ์ไม่พึ่งบริบท G กำกวมหรือไม่"
เป็นปัญหาที่ตัดสินไม่ได้
ทฤษฎีบท : ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่จะตรวจสอบว่า ไวยากรณ์ไม่พึ่งบริบท G1
และ G2 ใด ๆ L(G1)  L(G2) = Ø หรือไม่"
เป็นปัญหาที่ตัดสินไม่ได้ L(G2) = Ø หรือไม่"
เป็นปัญหาที่ตัดสินไม่ได้
ทฤษฎีบทของกรายบาค : (Greibach's theorem) ให้ 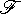 เป็นกลุ่มของภาษาที่มาจากชุดตัวอักษรโดยมีสมบัติว่า
เป็นกลุ่มของภาษาที่มาจากชุดตัวอักษรโดยมีสมบัติว่า
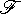 มีสมบัติปิดภายใต้การเขียนต่อกันกับเซตปกติ และมีสมมบัติปิดภายใต้การผนวก (union) และ มีสมบัติปิดภายใต้การเขียนต่อกันกับเซตปกติ และมีสมมบัติปิดภายใต้การผนวก (union) และ
- สำหรับแต่ละสายอักขระ w
  *
ปัญหาที่ถามว่า "มีหรือไม่มี ขั้นตอนวิธีที่จะตรวจสอบว่า สำหรับ L ใด ๆ ใน *
ปัญหาที่ถามว่า "มีหรือไม่มี ขั้นตอนวิธีที่จะตรวจสอบว่า สำหรับ L ใด ๆ ใน 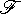 ที่ L ที่ L
  *, L = *, L =
 * หรือไม่" เป็นปัญหาที่ตัดสินไม่ได้ * หรือไม่" เป็นปัญหาที่ตัดสินไม่ได้
ถ้า 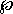 
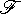 และ และ 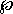
 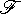 และ และ
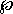 มีสมบัติว่า มีสมบัติว่า
- เซตปกติทุกเซตเป็นสมาชิกของ
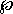 และ และ
- สำหรับทุกภาษา L และทุก a
 L ถ้า L L ถ้า L
 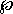 แล้ว L/a แล้ว L/a
 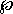 ด้วย ด้วย
จะได้ว่า ปัญหาที่ถามว่า "มีหรือไม่มี ขั้นตอนวิธีที่จะตรวจสอบว่า สำหรับ L ใด ๆ ใน 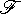 , L , L
 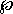 หรือไม่" เป็นปัญหาที่ตัดสินไม่ได้ หรือไม่" เป็นปัญหาที่ตัดสินไม่ได้
ทฤษฎีบท : ปัญหาที่ถามว่า "มีหรือไม่มีขั้นตอนวิธีที่จะตรวจสอบว่า ไวยากรณ์ไม่พึ่งบริบท G ใด ๆ
L(G) เป็นเซตปกติหรือไม่" เป็นปัญหาที่ตัดสินไม่ได้
|
|