ฟังก์ชันรีเคอร์ซีฟปฐมฐาน (Primitive recursive function)
จากความสามารถของเครื่องทัวริงที่ผ่านมา เราอยากทราบว่าภาษาที่เครื่องเหล่านี้ยอมรับคือภาษาประเภทใด
ในบทนี้เราจะสนใจฟังก์ชันแทนการอธิบายภาษา เราสามารถมองเครื่องทัวริงว่ามีความสามารถในการคำนวณฟังก์ชันโดยที่
สายอักขระบนแถบข้อมูลรับเข้าแทนสมาชิกในโดเมนของฟังก์ชัน และเมื่อจบการทำงาน สายอักขระที่ปรากฎบนแถบข้อมูลนั้น
แทนค่าของฟังก์ชันที่ได้ เราเรียกเครื่องทัวริงที่คำนวณค่าฟังก์ชันได้ว่า ฟังก์ชันทัวริง-คำนวณได้ (Turing computable function)
บทนิยาม : เรากล่าวว่า ฟังก์ชัน f เป็น ฟังก์ชันเริ่มต้น (initial function) ก็ต่อเมื่อ
- f :
 0 0 
 0 โดยที่ f(x) = x + 1 ทุก x 0 โดยที่ f(x) = x + 1 ทุก x
  0 เราเขียนแทน f
ด้วย S เรียกว่า ฟังก์ชันตัวตามหลัง (successor function) 0 เราเขียนแทน f
ด้วย S เรียกว่า ฟังก์ชันตัวตามหลัง (successor function)
- f:
 0 0 
 0 และมี c 0 และมี c 
 0 ที่ f(x) = c ทุก x 0 ที่ f(x) = c ทุก x 
 0 เราเรียกฟังก์ชันนี้ว่า ฟังก์ชันค่าคงตัว (constant function) 0 เราเรียกฟังก์ชันนี้ว่า ฟังก์ชันค่าคงตัว (constant function)
- f :
 0k 0k
  0 โดยที่ k 0 โดยที่ k
  และมี i และมี i
 {1, 2, 3, ..., k} ที่ f(x1, x2, ...,
xk) = xi ทุก (x1, x2, ..., xk) {1, 2, 3, ..., k} ที่ f(x1, x2, ...,
xk) = xi ทุก (x1, x2, ..., xk)
  0k
ในกรณีนี้เราเรียก f ว่า ฟังก์ชันภาพฉายตำแหน่งที่ i (i-th projection function) โดยมากนิยมเขียนแทนด้วย 0k
ในกรณีนี้เราเรียก f ว่า ฟังก์ชันภาพฉายตำแหน่งที่ i (i-th projection function) โดยมากนิยมเขียนแทนด้วย
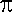 ik ik
เราสามารถสร้างฟังก์ชันที่คำนวณค่าต่างๆ ได้จากการแทนค่าฟังก์ชัน คือ
บทนิยาม : ให้ k, m 
 และ g : และ g :  0k 0k
  0, f : 0, f :
 0m 0m 
 0 และสำหรับแต่ละ i 0 และสำหรับแต่ละ i  {1, 2, ..., k},
hi : {1, 2, ..., k},
hi :  0m 0m 
 0 0
เราจะกล่าวว่า f ได้จาก g และ h1, h2, ..., hk
โดยการแทนค่า ก็ต่อเมื่อ f(x1, x2, ..., xm) =
g(h1(x1, x2, ..., xm),
h2(x1, x2, ..., xm) , ...,
hk(x1, x2, ..., xm)) ทุก
(x1, x2, ..., xm) 
 0m 0m
บทนิยาม : ให้ f, g, h เป็นฟังก์ชัน เรากล่าวว่า f ได้จาก g และ
h โดยรีเคอร์ชันปฐมฐาน (primitive recursion) ก็ต่อเมื่อ
- f:
 0 0 
 0, g เป็นฟังก์ชันค่าคงตัว, h : 0, g เป็นฟังก์ชันค่าคงตัว, h :
 02 02 
 0 โดยที่ 0 โดยที่
- f(0) = g(0)
- f(y + 1) = h(y, f(y)) ทุก y
  0 0
- หรือ f:
 0m+1 0m+1
  0, g : 0, g :
 0m 0m 
 0, h : 0, h :
 0m+2 0m+2 
 0 โดยที่ 0 โดยที่
- f(x1, x2, ..., xm, 0) = g(x1,
x2, ..., xm)
- f(x1, x2, ...,
xm, y + 1) = h(x1, x2, ..., xm, y,
f(x1, x2, ..., xm, y)) ทุก y
  0 0
บทนิยาม : ฟังก์ชันรีเคอร์ซีฟปฐมฐาน (primitive recursive function) เป็นฟังก์ชันที่นิยามโดยวิธีเรียกซ้ำดังนี้
- ฟังก์ชันเริ่มต้นทุกฟังก์ชันเป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน
- ถ้า g, h1, h2, ..., hk เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐานแล้ว ฟังก์ชันที่ได้จาก
g, h1, ..., hk โดยการแทนค่า จะเป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน
- ถ้า g, h เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐานแล้ว ฟังก์ชันที่ได้จาก g และ h โดยรีเคอร์ชันปฐมฐาน
จะเป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน
และฟังก์ชันรีเคอร์ซีฟปฐมฐานมีเพียงที่กล่าวข้างต้นเท่านั้น
ทฤษฎีบท : ถ้า f และ g เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน และพิสัยของ f เป็นสับเซตของโดเมนของ
g แล้ว g 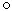 f จะเป็นฟังก์ชันรีเคอร์ซีฟปฐมฐานด้วย f จะเป็นฟังก์ชันรีเคอร์ซีฟปฐมฐานด้วย
ตัวอย่างที่ 1: ฟังก์ชันเอกลักษณ์, I :  0 0
  0 นิยามโดย I(x)
= x ทุก x 0 นิยามโดย I(x)
= x ทุก x   0
เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน 0
เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน
ตัวอย่างที่ 2: ฟังก์ชันการบวกจำนวนนับรวมศูนย์, h+ :
 02 02 
 0 นิยามโดย h+(x, y) = x + y ทุก x,
y 0 นิยามโดย h+(x, y) = x + y ทุก x,
y   0
เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน 0
เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน
ตัวอย่างที่ 3: ฟังก์ชันการคูณจำนวนนับรวมศูนย์, h* :
 02 02 
 0 นิยามโดย h*(x, y) = xy ทุก x, y 0 นิยามโดย h*(x, y) = xy ทุก x, y
  0
เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน 0
เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน
ตัวอย่างที่ 4: ฟังก์ชันตัวนำหน้า (predecessor function), D :
 0 0 
 0 นิยามโดย D(0) = 0 และ D(n+1) = n
ทุก n 0 นิยามโดย D(0) = 0 และ D(n+1) = n
ทุก n   0
เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน 0
เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน
ตัวอย่างที่ 5: ฟังก์ชัน f :
 02 02 
 0 นิยามโดย f(m, n) = m - n ถ้า m 0 นิยามโดย f(m, n) = m - n ถ้า m
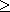 n และเท่ากับศูนย์ในกรณีอื่น ๆ เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน n และเท่ากับศูนย์ในกรณีอื่น ๆ เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน
จากฟังก์ชันที่นิยามทั้งหมด เราพบว่าโดเมนของฟังก์ชันเหล่านั้นจะเท่ากับ  0n
สำหรับฟังก์ชันบางประเภท เราอาจอยากให้คำนวณค่าของฟังก์ชันเฉพาะบางค่าใน 0n
สำหรับฟังก์ชันบางประเภท เราอาจอยากให้คำนวณค่าของฟังก์ชันเฉพาะบางค่าใน  0n
ตัวอย่างเช่นฟังก์ชันตัวนำหน้า เราอยากนิยามทุกค่าบน 0n
ตัวอย่างเช่นฟังก์ชันตัวนำหน้า เราอยากนิยามทุกค่าบน  ที่ไม่ใช่ 0 เราทำได้โดย ที่ไม่ใช่ 0 เราทำได้โดย
บทนิยาม : ให้ m 
 0, g : 0, g :
 0m+1 0m+1 
 0, f เป็นฟังก์ชัน เรากล่าวว่า f ได้จาก g โดยการหาค่าน้อยสุด
(minimalization) ก็ต่อเมื่อ สำหรับแต่ละ (x1, x2, ..., xm) 0, f เป็นฟังก์ชัน เรากล่าวว่า f ได้จาก g โดยการหาค่าน้อยสุด
(minimalization) ก็ต่อเมื่อ สำหรับแต่ละ (x1, x2, ..., xm)
  0m 0m
- f(x1, x2, ..., xm) = ค่าน้อยที่สุดของเซต { y
  0 | g(x1,
x2, ..., xm, y) = 0} 0 | g(x1,
x2, ..., xm, y) = 0}
บทนิยาม : ฟังก์ชันรีเคอร์ซีฟ (recursive function) เป็นฟังก์ชันที่นิยามโดยวิธีเรียกซ้ำดังนี้
- ฟังก์ชันรีเคอร์ซีฟปฐมฐานทุกฟังก์ชันเป็นฟังก์ชันรีเคอร์ซีฟ
- ถ้า g, h1, h2, ..., hk เป็นฟังก์ชันรีเคอร์ซีฟ แล้ว
ฟังก์ชันที่ได้จาก g, h1, h2, ..., hk โดยการแทนค่า จะเป็นฟังก์ชันรีเคอร์ซีฟ
- ถ้า g, h เป็นฟังก์ชันรีเคอร์ซีฟ แล้วฟังก์ชันที่ได้จาก g และ h โดยรีเคอร์ชันปฐมฐาน จะเป็นฟังก์ชันรีเคอร์ซีฟ
- ถ้า g เป็นฟังก์ชันรีเคอร์ซีฟ แล้วฟังก์ชันที่ได้จาก g โดยการหาค่าน้อยสุด จะเป็นฟังก์ชันรีเคอร์ซีฟ
และฟังก์ชันรีเคอร์ซีฟต้องได้จากกฎสี่ข้อนี้เท่านั้น
ตัวอย่างที่ 6 : จงแสดงว่า f0 = {0}  {0} เป็นฟังก์ชันรีเคอร์ซีฟ {0} เป็นฟังก์ชันรีเคอร์ซีฟ
ตัวอย่างที่ 7 : จงแสดงว่า f4 = 
  0 ที่นิยามโดย
f4(n) = n-1 ทุก n 0 ที่นิยามโดย
f4(n) = n-1 ทุก n 
 เป็นฟังก์ชันรีเคอร์ซีฟ เป็นฟังก์ชันรีเคอร์ซีฟ
ทฤษฎีบท :
- ถ้า f เป็นฟังก์ชันรีเคอร์ซีฟปฐมฐาน แล้ว จะมีเครื่องทัวริง M ที่คำนวณค่าของฟังก์ชัน f โดยเครื่องนี้หยุด (halt) การทำงานเสมอ
เมื่ออ่านสายอักขระรับเข้าใด ๆ
- f เป็นฟังก์ชันรีเคอร์ซีฟ ก็ต่อเมื่อ มีเครื่องทัวริง M ที่คำนวณค่าของฟังก์ชัน f โดยเครื่องนี้หยุด (halt) การทำงานเสมอ
เมื่ออ่านสายอักขระรับเข้า ภายในโดเมนของฟังก์ชัน และอาจไม่หยุดในกรณีอื่น ๆ
ข้อสังเกต ฟังก์ชันรีเคอร์ซีฟ แตกต่างกับฟังก์ชันรีเคอร์ซีฟปฐมฐานที่โดเมนของฟังก์ชันรีเคอร์ซีฟ อาจเป็นทั้ง
 0k หรือสับเซตของ 0k หรือสับเซตของ  0k 0k
บทกลับของทฤษฎีบทอาจไม่จริง นั่นคือ ถ้าเรามีเครื่องทัวริง M ที่คำนวณค่าของฟังก์ชัน f โดยที่เครื่องนี้หยุดเสมอ ฟังก์ชันที่ได้อาจไม่ใช่ฟังก์ชันรีเคอร์ซีฟปฐมฐาน
ตัวอย่างของฟังก์ชันที่ไม่ใช่ฟังก์ชันรีเคอร์ชีฟปฐมฐาน และมีเครื่องทัวริง M ที่หยุดเสมอที่คำนวณค่าฟังก์ชันนี้ได้ คือฟังก์ชันของแอคเคอร์มานน์
(Ackermann's function) A :  02 02
  0 ที่นิยามโดย 0 ที่นิยามโดย
- A(0, y) = 1 ทุก y

 0 0
- A(1, 0) = 2
- A(x, 0) = x + 2 ทุกจำนวนนับ x
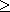 2 2
- A(x+1, y+1) = A(A(x, y+1), y) ทุก x, y

 0 0
เซตรีเคอร์ซีฟและเซตอาร์อี (Recursive sets and R.E. sets)
จากฟังก์ชันรีเคอร์ซีฟที่กล่าวมา เราจะสนใจเครื่องทัวริงที่มีสมบัติในการคำนวณฟังก์ชัน ในส่วนนี้เราจะกลับมาสนใจเครื่องทัวริงที่สามารถ
ตัดสินว่าสมาชิกใดอยู่หรือไม่อยู่ในเซต
บทนิยาม : ให้ L 
 * เรากล่าวว่า L เป็น เซตที่แจงนับได้แบบรีเคอร์ซีฟ (recursively enumerable
set) หรือเรียกสั้น ๆ ว่า เซตอาร์อี (R.E. set) ก็ต่อเมื่อ มีเครื่องทัวริง M อย่างน้อยหนึ่งเครื่องที่ยอมรับ L * เรากล่าวว่า L เป็น เซตที่แจงนับได้แบบรีเคอร์ซีฟ (recursively enumerable
set) หรือเรียกสั้น ๆ ว่า เซตอาร์อี (R.E. set) ก็ต่อเมื่อ มีเครื่องทัวริง M อย่างน้อยหนึ่งเครื่องที่ยอมรับ L
และ L เป็นเซตรีเคอร์ซีฟ (recursive set) ก็ต่อเมื่อ ทั้ง L และ 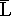 เป็นเซตอาร์อี เป็นเซตอาร์อี
ทฤษฎีบท : L เป็นเซตรีเคอร์ซีฟ ก็ต่อเมื่อ มีเครื่องทัวริง M อย่างน้อยหนึ่งเครื่องที่ยอมรับ L และ M หยุดการทำงานเสมอ
เมื่ออ่านสายอักขระรับเข้าใด ๆ
ข้อสังเกต
- L เป็นเซตรีเคอร์ซีฟ ก็ต่อเมื่อ
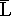 เป็นเซตรีเคอร์ซีฟ เป็นเซตรีเคอร์ซีฟ
- เซตรีเคอร์ซีฟทุกเซต เป็นเซตอาร์อี
ตัวอย่างที่ 8 : จงแสดงว่า L = {0n1n | n 
 0} เป็นเซตรีเคอร์ซีฟ 0} เป็นเซตรีเคอร์ซีฟ
ตัวอย่างที่ 9: จงแสดงว่า L = Ø เป็นเซตรีเคอร์ซีฟ
ตัวอย่างที่ 10: จงแสดงว่า  * เป็นเซตรีเคอร์ซีฟ * เป็นเซตรีเคอร์ซีฟ
ตัวอย่างที่ 11: จงแสดงว่า 0+ เป็นเซตรีเคอร์ซีฟ
ตัวอย่างที่กล่าวมาทั้งหมดเป็นเซตรีเคอร์ซีฟ คำถามที่มีต่อมาคือ มีเซตใดหรือไม่ที่ไม่ใช่เซตรีเคอร์ซีฟ เราจะสร้างเซต Ld
โดยใช้หลักตรรกศาสตร์และแสดงว่า เซตนี้ไม่เป็นเซตอาร์อี จากนั้นเราจะได้ว่า เซต Lu ไม่เป็นเซตรีเคอร์ซีฟ แต่เป็นเซตอาร์อี
ทฤษฎีบทประกอบ : สำหรับแต่ละ  ที่กำหนดให้ และแต่ละ
k ที่กำหนดให้ และแต่ละ
k   , ,
- TM = {M | M เป็นเครื่องทัวริง และ M มีสถานะทั้งหมด k สถานะ}
มีจำนวนสมาชิกทั้งหมดไม่เกิน (1 + 3k | |)^(k
| |)^(k
| |) |)
ทฤษฎีบท : สำหรับแต่ละ  ที่กำหนดให้ จะมีฟังก์ชัน ที่กำหนดให้ จะมีฟังก์ชัน
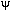 ซึ่งเป็นฟังก์ชัน 1-1 จาก ซึ่งเป็นฟังก์ชัน 1-1 จาก  ไปทั่วถึง TM
(TM เป็นเซตนับได้) ไปทั่วถึง TM
(TM เป็นเซตนับได้)
บทนิยาม : สำหรับแต่ละ  ที่กำหนดให้ และ ที่กำหนดให้ และ
 = {0, 1, = {0, 1,  , Z0}
เราสามารถจัดเรียงสมาชิกใน , Z0}
เราสามารถจัดเรียงสมาชิกใน  * โดยวิธีลำดับอักษรได้โดย * โดยวิธีลำดับอักษรได้โดย
 < 0 < 1 < 00 < 01 < 10 < 11 < 000 < 001
< ... < 0 < 1 < 00 < 01 < 10 < 11 < 000 < 001
< ...
ถ้าสำหรับแต่ละ i   ให้ wi
แทนสมาชิกตัวที่ i ของลำดับข้างต้น และสำหรับแต่ละ j ให้ wi
แทนสมาชิกตัวที่ i ของลำดับข้างต้น และสำหรับแต่ละ j 
 ให้ Mj เป็นเครื่องทัวริงที่ตรงกับ ให้ Mj เป็นเครื่องทัวริงที่ตรงกับ 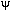 (j)
ในทฤษฎีบทที่แล้ว เราจะนิยาม ภาษาแนวทแยง (diagonal language) Ld ดังนี้ (j)
ในทฤษฎีบทที่แล้ว เราจะนิยาม ภาษาแนวทแยง (diagonal language) Ld ดังนี้
- Ld = {wi

 * | Mi ไม่ยอมรับ wi, i * | Mi ไม่ยอมรับ wi, i
  } }
ทฤษฎีบท : Ld ไม่เป็นเซตอาร์อี
ทฤษฎีบท : Lu = { <M,w> | M เป็นเครื่องทัวริง w
 {0,1}* และ M ยอมรับ w} เป็นเซตอาร์อี แต่ไม่เป็นเซตรีเคอร์ซีฟ {0,1}* และ M ยอมรับ w} เป็นเซตอาร์อี แต่ไม่เป็นเซตรีเคอร์ซีฟ
ทฤษฎีบท : ให้ L1 และ L2 
 * *
- ถ้า L1 และ L2 เป็นเซตอาร์อี แล้ว L1
 L2 และ L1
L2 และ L1  L2 เป็นเซตอาร์อี L2 เป็นเซตอาร์อี
- ถ้า L1 และ L2 เป็นเซตรีเคอร์ซีฟ แล้ว L1
 L2 และ L1
L2 และ L1  L2 เป็นเซตรีเคอร์ซีฟ L2 เป็นเซตรีเคอร์ซีฟ
ตัวอย่างที่ 12 : จงพิจารณาว่าข้อความต่อไปนี้จริงหรือเท็จ และแสดงการพิสูจน์
- ถ้า L1 และ L2 เป็นเซตอาร์อี แล้ว L1 - L2 เป็นเซตอาร์อี
- ถ้า L1 และ L2 เป็นเซตรีเคอร์ซีฟ แล้ว L1 - L2 เป็นเซตรีเคอร์ซีฟ
- ถ้า L1, L2, L3 เป็นเซตรีเคอร์ซีฟ แล้ว
 - (L2
- (L2  L3) เป็นเซตรีเคอร์ซีฟ L3) เป็นเซตรีเคอร์ซีฟ
|