Lecture 1:Introduction

Written byKrung Sinapiromsaran
July 2557



Box - Page - Convex - Zoom - Linear - Fade - None - Default

Outline

  • Course plan
  • Course definition for an algorithm
  • Different between instructions, algorithms, processes
  • Expressing algorithm
  • Problem specification
  • Algorithm Correctness
  • Loop invariant
  • Counter examples
  • Reason for the analysis of an algorithm

Objective

  • Understand terms and methodologies in Computer Science
  • Know the origin of the word “Algorithm” and its informal definition
  • Differentiate between step-by-step instructions / algorithms / processes
  • Identify the specification of a problem
  • Prove the correctness and give counter examples
  • Give reason for the analysis of an algorithm

Three main components of this course

  • Mathematical tools for analyzing algorithm
  • Study of common algorithms and data structures
  • Study of algorithm design strategies by examples

Course Philosophy

Aside from

  • Mathematical tools for analyzing algorithm
  • Study of common algorithms and data structures
  • Study of algorithm design strategies by examples

You will need to learn using

  • Neutral language for studying algorithms -- English/pseudocode
  • Standard algorithms (Learn by examples)
  • Group effort (Learn in team)

Course text book

Smiley face T.H. Cormen et al. Introduction to Algorithms. MIT Press, 2001.

  A lot of theorems and examples
  Contains a lot of good references
  Very useful for Computer Scientists
  Need to have one (paper back or electronics)

References

Smiley face K. Mehlhorn and P. Sanders. Algorithms and Data Structures: The Basic Toolbox. Springer, 2008.

  B.R. Preiss. Data Structures and Algorithms with Object-oriented Design Patterns in Java. Wiley, 1999. (+ other Java-specific texts)
  R. Sedgewick. Algorithms. Addison Wesley, 1988.
  S.S. Skiena. The Algorithm Design Manual. Springer, 2008.

References

Smiley face D.E. Knuth. The Art of Computer Programming. Addison Wesley, 1997. (In 3 volumes)
  “If you think you’re a really good programmer, read Knuth’s Art of Computer Programming. You should definitely send me a resume if you can read the whole thing.”
Bill Gates

What is an algorithm?

Smiley face Muhammad ibn Mūsā al-Khwārizmī
“algorism” referred to rules of performing arithmetic using Arabic numerals
Evolved into “algorithm” and came to mean a definite procedure for solving a problem or performing a task
“the idea behind any reasonable computer program”
Something like a recipe, process, method, technique, procedure, routine etc

What is an algorithm?

No formal definition has been accepted for all branches of Computer Science

  1. Finiteness: Must terminate after a finite number of steps.
  2. Definiteness: Each step must be precisely defined (rigourous, unambiguous). Programming languages are designed for specifying algorithms – every statement has a definite meaning.
  3. Input: Zero or more inputs.
    Q: Are there any useful algorithms with no inputs?
  4. Output: One or more outputs.
    Q: Are there any useful algorithms with no outputs?
  5. Effectiveness: Operations must be sufficiently basic that they can be done exactly and in a finite length of time, i.e. computable or do-able.

Valid algorithm?

According to our criteria, is the following statements valid algorithm?

Valid algorithm?

According to our criteria, is the following statements valid algorithm?

  • Not valid (definiteness): “pinch of salt” “beat lightly” “mix well” “even overnight”
  • All ambiguous
  • As cooks, we can interpret approximately what is meant, but not precise enough for a computer to understand

Valid algorithm?

According to our criteria, is the following statements valid algorithm?

Valid algorithm?

According to our criteria, is the following statements valid algorithm?

  • Not valid (Efficient): $10^{43}$ possible game states -- although finite, not realistic to evaluate all
  • If we can evaluate 1 million states per second, we will need $3.2 \times 10^{29}$ years!
  • Earth is about $4.5 \times 10^9$ years old

Valid algorithm?

According to our criteria, is the following statements valid algorithm?

Valid algorithm?

According to our criteria, is the following statements valid algorithm?

  • Valid
  • This is our first algorithm
  • One of the oldest known algorithms (300 BC) described by Euclid (in a slightly different form)

Implement using Python

Valid algorithm?

According to our criteria, is the following statements valid algorithm?

Valid algorithm?

According to our criteria, is the following statements valid algorithm?

  • Not valid (effectiveness)
  • No such function $f(n)$ is known
  • Until someone finds such a function, 1 is not an effective operation

Practical algorithm

In practice we want algorithms that are:

  • Correct
  • Efficient
  • Easy to implement
May not be simultaneously achievable.

Specification

  • An algorithm is an implementation of a solution to a problem
  • We need a way to specify a problem so we can design algorithms to solve it.
  • A computer program is a translation of an algorithm into a particular programming language (also an implementation)
  • Checking that an implementation correctly executes an algorithm is the realms of software engineering and formal methods
  • We are interested in the design and analysis of algorithms
  • We don’t care what language it is subsequently implemented in
  • But we do need a language to express algorithms

Q: Why don’t we always use English? Why don’t we program computers in English?

Expressing Algorithm

  1. English
  2. Pseudocode
  3. A programming language

Expressing Algorithm

We will use a mixture of English and pseudocode.

  • Pseudocode represents a good balance between precision and readability
  • Should be straightforward to translate to any programming language.
  • It’s intuitive - shouldn’t need to learn it.

Pseudocode of GCD

The algorithm for finding the greatest common divisor given above can be expressed in pseudocode as follows: Exercise: try it out – for different input values, trace the operation of the algorithm keeping track of current values of the variables

Python code of GCD

Specification and correctness

As algorists, we need tools to:

  • Specify a problem so we can design algorithms to solve it
  • Distinguish correct algorithms from incorrect ones
  • Compare algorithms and choose the “best” one

Problem Specification

A very common (and useful) informal way to specify a problem is to list its inputs and outputs:
Sorting:
Input:A sequence of $n$ numbers; $a_1, a_2, ..., a_n$
Output:A permutation, $i_1, i_2, ..., i_n$ of the input sequence such that \[ a_{i_1} \leq a_{i_2} \leq ... \leq a_{i_n} \]

Simple Specification

  • Definition: A simple specification is a pair of predicates, one describing the starting states, the precondition, and one describing the associated final state, the postcondition.
  • Factorial computational problem:
    Precondition: $n \in \mathbb{N}$; Postcondition: $r$ = $n!$
  • Sum from 1 to n computational problem:
    Precondition: $n \in \mathbb{N}$; Postcondition: $r$ = $\displaystyle\sum_{i = 1}^{n} i$.
  • Preconditions and postconditions are like a contract between the caller and the algorithm:
  • Algorithm: “If you ensure the precondition is satisfied, I’ll guarantee that the postcondition is satisfied upon termination”
  • Caller: “Ok, and if I don’t ensure the precondition is satisfied I’ll make no assumptions about what your behaviour will be”

GCD Specification

  • Let’s think up pre/postconditions for the greatest common divisor algorithm:
  • Precondition: $m, n \in \mathbb{N} \& (m > 0) \mbox{ and } (n > 0)$
    Postcondition: $(r|m)$ and $(r|n)$ amd $\forall i \in \mathbb{N}; (i|m) \mbox{ and } (i|n) \rightarrow i \leq r$.

Certifying GCD Algorithm

  • Sometimes preconditions and postconditions can be easily checked
  • Many programming languages support assertions – good practice to check pre/postconditions, example:

Certifying Algorithms

  • This might seem a bit circular – isn’t checking the postcondition as hard as running the algorithm in the first place?
  • In many situations checking assertions can be simplified by computing additional information – a certificate
  • A certifying algorithm computes a certificate for the postcondition
  • We will see examples of algorithms later where a certificate can be computed without affecting the efficiency of the algorithm

Loop invariant

  • A loop invariant is a statement which is true before and after each loop iteration
  • Used to help prove program correctness
  • Helps to clarify purpose of iterative structure
  • Loop variant ensures progress is made

Reasoning about correctness

  • We need to know whether our algorithm will always work, i.e. produce the correct/optimal answer.
  • Let’s look at an example:

    Robot Tour Optimization

    Robot arm must visit a set of contact points on a circuit board to solder each point Need to choose an order in which the contact points will be visited We want to minimise time taken, i.e. shortest path Shorter tour = faster production = cheaper to produce = more profit

Nearest neighbor heuristic

Down arrow

Input: A set $P$ of $n$ points
Output: The shortest cycle tour that visits each point

  • Simple idea: nearest neighbor tour
  • Use a heuristic – pick any starting point, then next move is always to nearest point

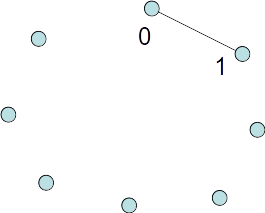
Tour with nearest neighbor heuristic

Tour example

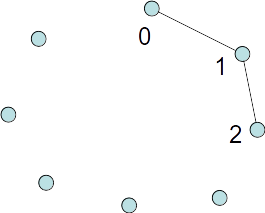
Down arrow

Tour example

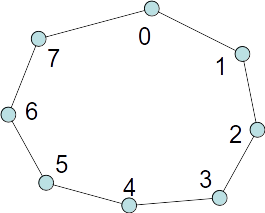
Down arrow

Tour example

Down arrow

Tour example

Down arrow

Look encouraging

Tour example

Down arrow

  • Look encouraging
  • Optimal for this instance!
  • Q:Always optimal?
  • Q:What is needed to prove incorrectness?

Counter tour example

An instance where nearest neighbor gives a suboptimal solution

Down arrow

Tour example

Down arrow

Counter tour example

Down arrow

Counter tour example

Down arrow

Counter tour example

Down arrow

Counter tour example

Down arrow

Counter tour example

A better (optimal) solution for the same instance:
Down arrow
Down arrow

  • It can be easy to prove that an algorithm is not correct – just find a counter example (the simpler, the better)
  • Counter example = instance of problem + optimal solution + demonstration that algorithm produces a less optimal solution
  • Lack of a counter example doesn’t prove it works
  • We will not study the formal methods to prove correctness of our algorithms
  • Instead, we will informally convince ourselves that they work

Specification and correctness

As algorists, we need tools to:

  • Specify a problem so we can design algorithms to solve it and strategies to design algorithms which satisfy specifications
  • Distinguish correct algorithms from incorrect ones
  • Check that the algorithm satisfies the problem specification
  • Compare algorithms and choose the “best” one
  • There may be many alternative algorithms that satisfy a specification
  • We want the one that is “best” for our purposes
  • Often, best = most efficient. Is this always the case?
  • The subject of much of this course!

Analysis of algorithms

The theoretical study of computer program performance and resource usages.

  • Is performance the most important measure of an algorithm?
  • What’s more important than performance? correctness; security; user-friendliness; maintainability; robustness/reliability; functionality/features; simplicity; programmer time; modularity; extensibility
  • Performance is the currency of computation
  • We can use it to buy other things: functionality, user-friendliness etc.

Why study analysis of algorithms?

  • Some algorithms experts are lousy programmers, but no good programmer can be bad at algorithms
  • Algorithm design and analysis is the essence of what we do as computer scientists
  • With more sophisticated software engineering systems, the demand for mundane programmers will diminish
  • Soon all known algorithms will be available in libraries

Why study analysis of algorithms?

  • Great thinkers will always be needed: “I can develop a new algorithm for you”
  • “To be a good programmer you can either study programming for 10 years or take an algorithms course and study programming for 2 years”
  • Making things faster is fun! Some people try to design faster cars, we try to design faster algorithms!

Conclusion

  • What an algorithm is
  • How to specify a problem
  • How to show algorithm incorrectness by counter example
  • Some justification for why algorithm analysis is important

Comments and Suggestions