Lecture 4:Data Structure
Written byKrung Sinapiromsaran
July 2557
Outline
- Relationship between algorithms and data structures
- Physical memory
- Concrete versus Abstract data structure
- Contiguous versus Linked
- Dynamic arrays – amortized analysis
- Abstract Data Type (ADT)
- Linear abstract data types: lists, stacks, queues, deques
- Dictionaries
- Linear implementations of dictionaries
Objective
- Explain the relationship between algorithm and data structures
- Distinguish between concrete data structure and abstract data structure
- Analyze and explain contiguous and linked structure to implement ADT such as Stack, Queue, Deque
- Analyze the dictionary operations based on different implementation
Relationship between algorithm and data structure
- Our algorithms will operate on data. We need a way to store this data.
- We want to be able to perform abstract operations on this data:
- adding a student to an enrollment database
- searching for a student with a certain name
- listing all students taking a certain module
- Data structures are like the building blocks of algorithms
- Using abstract structures such as sets, lists, dictionaries, trees, graphs etc. let us think algorithmically at a more abstract level
- But, using a poor choice of data structure or a poor choice of implementation of a data structure can make your algorithm asymptotically worse
Relationship between algorithm and data structure
- Implementations of abstract data structures are now included in standard libraries of almost every programming language
- So you may well think:
“I’m never going to have to implement any of these concepts, why should I care about data structures?”
Answer part 1: This is good. Reinventing the wheel is pointless, such libraries will save you time.
Answer part 2: If you don’t know how the data structure is implemented, you won’t know the efficiency of different operations – this can drastically affect the running time of your algorithms - Understanding the mechanics of data structures is crucial to understanding algorithm efficiency and becoming a good designer of new algorithms
Physical memory
Fact:Store data structures in the memory of a computer
What does the memory of our computer look like?

- Organised into banks, rows, columns etc. We supply a bank number, row number etc (= an address), memory returns us the contents Address → contents
Physical memory
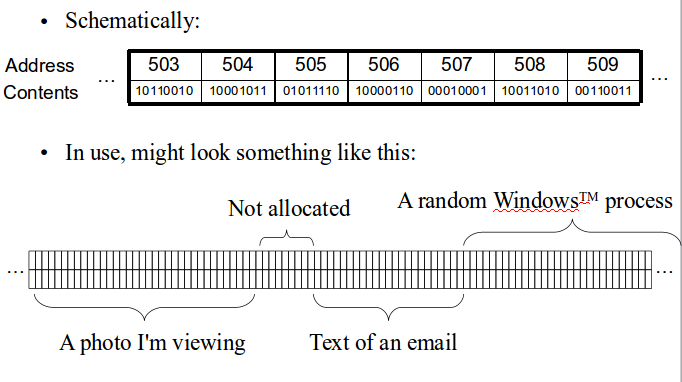
Concrete versus Abstract data structure
- We therefore have two levels of thinking about data structures:
Concrete: concerned with addresses in physical memory
Abstract: concerned only with abstract operations supported - Example:
Concrete: arrays, linked lists
Abstract: sets, lists, dictionaries, trees, graphs - But our implementations of abstractions must be in terms of the concrete structures with which our computer operates
Contiguous versus Linked
- We can subdivide concrete data structures into two classes:
- Contiguous: Composed of a single block of memory
- Linked: Composed of multiple distinct chunks of memory together by pointers
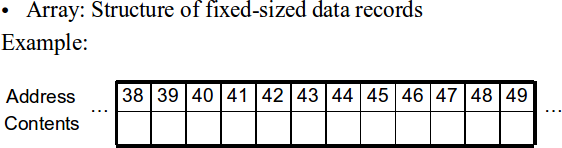
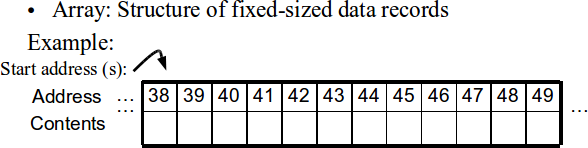
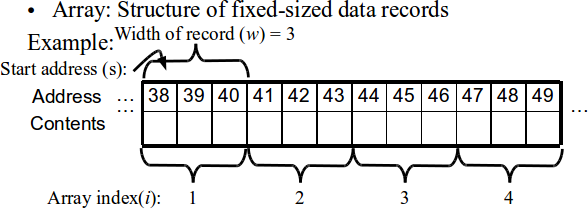
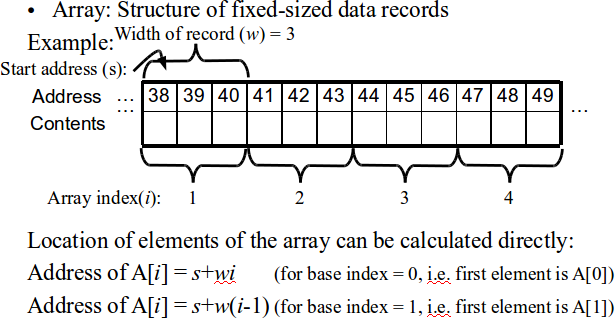
Contiguous data structures -- Arrays and Record
Contiguous data structures -- Arrays and Record
Contiguous data structures -- Arrays and Record
Contiguous data structures -- Arrays and Record
Benefits of using contiguous array structures
- We can retrieve an array element from its index in constant time, O(1), meaning it costs us asymptotically nothing to look up a record – this is a really big deal
- Consist solely of data, no space wasted on links
- Physical continuity/memory locality: if we look up element $i$, there is a high probability we will look up element $i+1$ next – this is exploited by cache memory in modern computer architectures
Drawbacks of using contiguous array structures
- Inflexible: we have to decide in advance how much space we want when the array is allocated
- Once the block of memory for the array has been allocated, that’s it – we’re stuck with the size we’ve got
- If we try to write past the end of the array (overflow), we’ll be intruding on memory allocated for something else causing a segmentation fault
- We can compensate by always allocating arrays larger than we think we’ll need, but this wastes a lot of space
- Inflexible: think about removing or inserting sequences of records in the middle of an array
Dynamic arrays
- A potential way around the problem of having to decide array size in advance is to use the dynamic arrays
- We could start with an array of size 1
- Each time we run out of space (i.e. want to write to index $m+1$ in an array of size $m$) we find a block of free memory, allocate a new array increasing the array size from $m$ to $2 m$ and copy all the contents across
- Q: If we currently have $n$ items in our dynamic array, how many doubling operations will we have executed so far?
- A: $⌈\log_2 n⌉$
- The expensive part is copying every element into the new larger array when we have to resize
- Q: How expensive is this?
- A: Linear: $O(n)$
Dynamic arrays
- The trickier question to answer is this
- Q: What is the worst case complexity of inserting into a dynamic array?
- A: It depends on whether we’ve filled up the array or not:
Not full: Just insert the element = O(1)
Full: Allocate new array, copy everything across, add new element = $O(n)$ - We can’t give a definitive answer on the worst case complexity – it depends!
Dynamic Arrays
Let's imagine we've just copied our data to a larger array:

- We can now make $n$ insertions at cost O(1) before we have to do anymore copying
- The $n+1^{th}$ insertion will cost us $2n$ = $O(n)$
- Total work for $n$ insertions is $3 n$.
- $n$ insertions into a dynamic array is complexity $O(n)$
- $n$ insertions into our standard array is also complexity $O(n)$ ...
Amortized analysis
- This sort of analysis is called amortized analysis
- Meaning: average cost of an operation over a sequence of operations
- Different to average-case analysis (which is averaging over probability distribution of possible inputs)
- Key idea of dynamic arrays: insertions will “usually” be fast, accessing elements will always be O(1)
- In Big Oh terms, a dynamic array is no more inefficient than a standard array
Linked Structures
- Alternative to contiguous structures are linked structures E.g. a linked list:

Linked Structures
- Alternative to contiguous structures are linked structures E.g. a linked list:

Linked Structures
- Alternative to contiguous structures are linked structures E.g. a linked list:
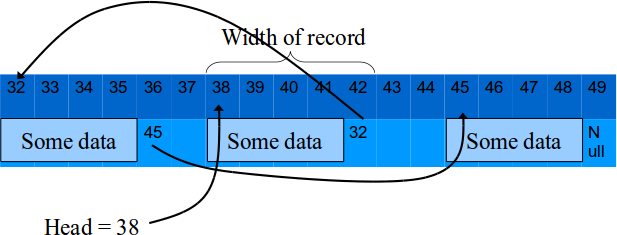
Linked Structures
- Alternative to contiguous structures are linked structures E.g. a linked list:
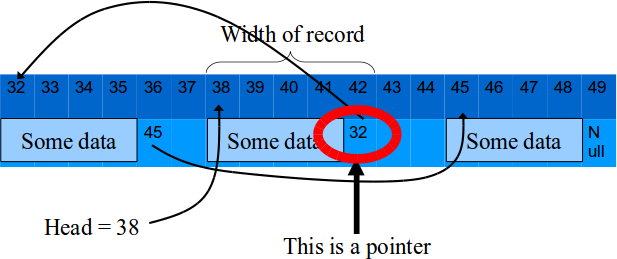
Schematic representation of linked structures

Schematic representation of linked structures

Alternative:Keep a pointer to the item before as well as after as Doubly linked list:

Benefits of using linked list structures
- We don’t need to worry about allocating space in advance, can use any free blocks of space in memory
- We only run out of space when the whole memory is actually full
- Very flexible: think about adding sublists or deleting items
- More efficient for moving large records (leave data in same place in memory, just change some pointers)
Drawbacks of using linked list structures
- Wasted space: we’re storing both pointers and data.
- To find the $p^{th}$ item, we must start at the beginning and follow pointers until we get there.
- In the worst case, if there are $n$ items in a list and we want the last one, we have to do $n$ lookups
- So retrieving an element from its position in the list is $O(n)$.
- This is a real problem.
Abstract Data Type
- We’ve seen concrete data structures which dealt with arranging data in memory
- Abstract Data Types offer a higher level view of our interactions with data
- Comprised of: (1) Data (2) Operations that allow us to interact with this data
- We describe the behaviour of our data structures in terms of abstract operations
- We can therefore use them without thinking:
“Add this item to this list, I don’t care how you do it or how you are storing the list”
Abstract Data Type
- However, the way these operations are implemented will affect efficiency.
- There are different implementations of the same abstract operations.
- We want the ones we will use most commonly to be the most efficient.
- We will look briefly at 3 ADTs today: stacks, queues and dictionaries
Stacks (Last-In First-Out:LIFO)
Queues (Last-in First-out
Queues (Last-in First-out)
- Operations:
- Queues crop up when we want to process items in the order they arrived.
- Later we will see that adding nodes of a tree to a stack or queue and then retrieving them results in different tree traversal strategies.
Deques
- Operations:
- More versatile variant of a queue
- Short for double-ended queue, pronounced “deck”
Stacks and Queues Implemented as Arrays
- Stacks as Arrays
- We only need to keep track of length
- Queues as Arrays
- We keep track of front and back index
- Exercise:think up similar instructions for list implementations
Stacks and Queues
- All operations on stacks and queues are O(1), implemented as either arrays or linked lists
- Poping an empty stack or dequeueing an empty queue is called underflow
- Trying to add an item when the memory limit of the chosen implementation has been reached is called overflow
Dictionary
- Perhaps the most important ADT is the dictionary
- An element in a dictionary contains two parts:
- A key – used to address an item
- A datum – associated with the key
- Keys are unique, the dictionary is a function from keys to data
- Think of our standard notion of a dictionary: key = word, datum = definition
- Dictionaries are of huge practical importance
- Google search is effectively a dictionary which pairs keywords with websites
Dictionary Operations
- Some common operations
- Others might include size(D), modify(D,k,v), IsEmpty(D) and so on
- Implementing dictionaries such that the above operations are efficient requires careful choice of ADT implementation
- Q: What will the complexity of there operations be if we implement them with an array or a linked list? Will the data being sorted make a difference?
Dictionary Operations
Complexity of dictionary operations implemented with an array for an $n$ entry dictionary:
| Dictionary Operations | Unsorted array | Sorted array |
|---|---|---|
| Lookup(D, k) | ||
| Insert(D, k) | ||
| Delete(D, k) | ||
| IsPresent(D, k) |
Dictionary Operations
Complexity of dictionary operations implemented with an array for an n entry dictionary:
| Dictionary Operations | Unsorted array | Sorted array |
|---|---|---|
| Lookup(D, k) | O($n$) | O($\log n$) |
| Insert(D, k) | O(1) | O($n$) |
| Delete(D, k) | O($n$) | O($n$) |
| IsPresent(D, k) | O($n$) | O($\log n$) |
- For a sorted array, we can use binary search to find an item
- Q: Can you explain the difference in cost for insert and delete?
- A: We have a higher cost maintaining the sorted list, when we insert or delete we have to shuffle up items above. In worst case this would be every entry
Dictionary Operations
Complexity of dictionary operations implemented with a linked list for an n entry dictionary:
| Dictionary Operations | Unsorted array | Sorted array |
|---|---|---|
| Lookup(D, k) | ||
| Insert(D, k) | ||
| Delete(D, k) | ||
| IsPresent(D, k) |
Dictionary Operations
Complexity of dictionary operations implemented with a linked list for an n entry dictionary:
| Dictionary Operations | Unsorted array | Sorted array |
|---|---|---|
| Lookup(D, k) | O($n$) | O($n$) |
| Insert(D, k) | O(1) | O($n$) |
| Delete(D, k) | O($n$) | O($n$) |
| IsPresent(D, k) | O($n$) | O($n$) |
- We can no longer use binary search to locate an item in the sorted case
- So we trade off the flexibility of a linked structure against reduced efficiency for lookup operations
Conclusion
- We’ve seen the difference between concrete and abstract, linked and contiguous
- We’ve seen some important examples of ADTs
- Linear implementations of dictionaries aren’t very efficient
- Using a sorted array makes dictionary lookups fast
Comments and Suggestions
- Assistant Professor Krung Sinapiromsaran
- Web: http://pioneer.netserv.chula.ac.th/~skrung
- Email: Krung.S@chula.ac.th