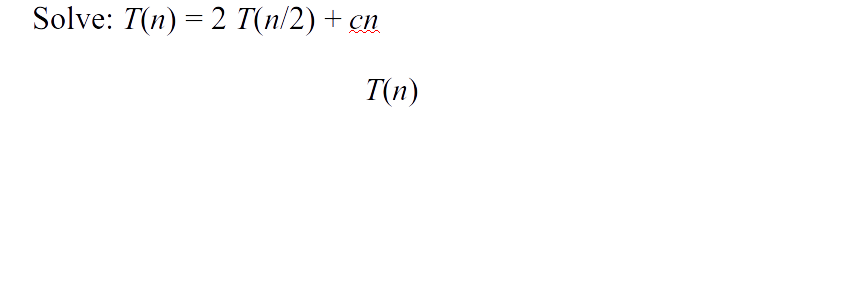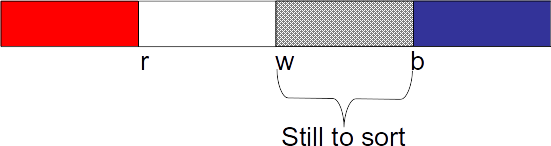Lecture 5:Sorting
Written byKrung Sinapiromsaran
July 2557
Outline
- What is sorting and why is it important?
- Simple quadratic sorts (selection and insertion sort)
- An O($n \log n$) sort using divide-and-conquer (merge sort)
- Limits of sorting – comparison-based algorithms
- Doing even better – non-comparison-based
Objective
- Be able to explain the usage of sorting in various problem
- Track the algorithm performance
- Analyze various sorting algorithms
- Compare sorting algorithms with respect to asymptotic notation
- Explain the limitation of comparison-based sorting algorithms
- Explain why some sorting algorithms can achieve a better running time
The problem of sorting
Input: A sequence $s$ = <$e_1, ..., e_n$> of $n$ elements
We make the following assumptions:
- Each element has an associated key: $k_i$ = key($e_i$)
- There is a linear order defined on the keys: $\leq$
- For ease of notation we write: \[e \leq e' \leftrightarrow key(e) \leq key(e')\]
Output:A sequence $s'$ = $\langle e'_1, ..., e'_n \rangle$ where $s'$ is a permutation of $s$
and $e'_1 \leq ... \leq e'_n$.
Sorting as a formal postcondition:
\[\forall i, j; 0 < i < j \leq n \rightarrow s'[i] < s'[j] \mbox{ and } bag(s) = bag(s')\]
Aside:Bags or Multisets
Two informal definitions of a bag or multiset:
- A bag is like a set, but a member of a bag can have more than one member.
- A bag is like a sequence with the order thrown away
Intuitive analogy: think of coins in your pocket - An element is either in a set or it isn’t.
- An element belongs to a bag zero or more times.
- The number of times an element belongs to a bag is its multiplicity.
- The total number of elements in a bag, including repeated memberships, is its cardinality.
Motivation
- Sorting is standard fodder for an introduction to algorithm course
- Good for teaching algorithm analysis, lots of alternative algorithms to compare, different algorithmic concepts (divide-and-conquer, randomised algorithms)
- However, is sorting still important in the real world problem?
Answer: yes, definitely! - According to Skiena, computers spend approx. 25% of their time sorting, so doing this efficiently is hugely important.
- New developments are still being made in this area (library sort in 2004, Ratio Based Stable In-Place Merging in 2008, Adjacent Pivot quicksort in 2010)
- There are a huge number of applications of sorting – it makes lots of other tasks possible or easier or more efficient.
Applications of Sorting
- Search preprocessing: we saw last time that sorting an array reduces searching from $O(n)$ to $O(\log n)$
- Selection: what is the $k^{th}$ largest element in a sequence? If it’s sorted, just pick element $k$.
- Convex hulls: what is the smallest polygon that encloses a set of points? (useful in geometric algorithms). To solve, sort points by x-coordinate, add from left to right, delete points when enclosed by polygon including new point.
- Closest pair: given a set of numbers, find the pair with the smallest difference between them. To solve: sort, then just do a linear scan through the sequence, keeping track of smallest distance so far.
- Interesting note: IBM was formed principally on being able to sort US census data
Relationship between algorithm and data structure
- Our algorithms will operate on data. So we need a way to store this data.
- Able to perform abstract operations:
- adding a student to an enrollment database
- searching for a student with a certain name
- listing all students taking a certain module
- Data structures are like the building blocks of algorithms.
- Using abstract structures such as sets, lists, dictionaries, trees, etc. let us think algorithmically at a more abstract level.
- But, using a poor choice of data structure or a poor choice of implementation of a data structure can make your algorithm asymptotically worse.
Relationship between algorithm and data structure
- Implementations of abstract data structures are now included in standard libraries of almost every programming language.
- “I’m never going to have to implement any of these concepts, why should I care about data structures?”
Answer part 1: This is good. Reinventing the wheel is pointless, such libraries will save you time.
Answer part 2: If you don’t know how the data structure is implemented, you won’t know the efficiency of different operations – affect the running time of your algorithms - Understanding the mechanics of data structures is crucial to understanding algorithm efficiency and becoming a good designer of new algorithms.
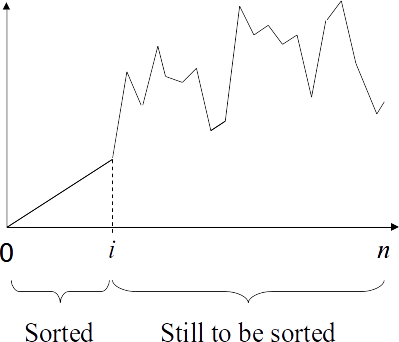
Hedgehog Diagram
A useful visualization of data:
Hedgehog Diagram
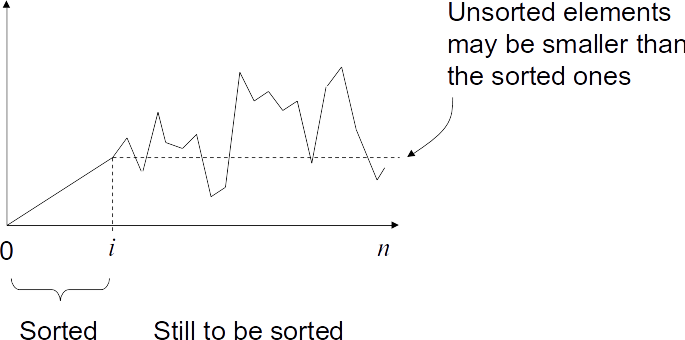
We can visualise the precondition and postcondition of the sorting problem in terms of these diagrams:
It can also be helpful to visualise the intermediate states of sorting algorithms using these diagrams – visualise the invariant preserved
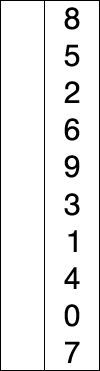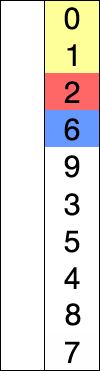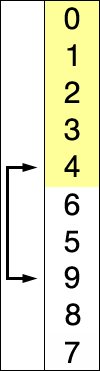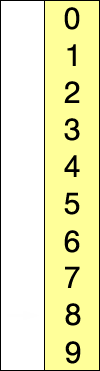
Selection sort concept
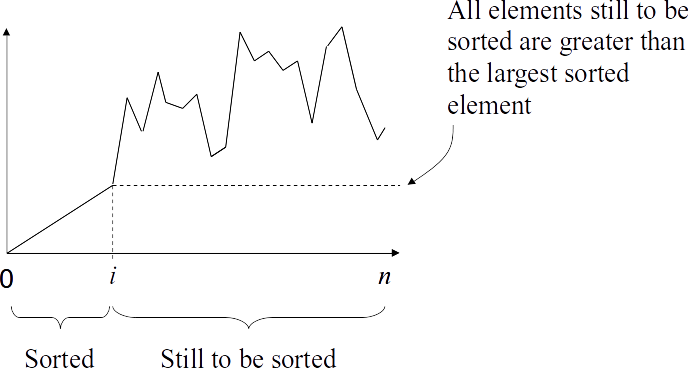
Our first sorting algorithm is selection sort. The idea is to maintain the following invariant:
- The partially sorted sequence consists of two parts:
The first part, which is already sorted.
The second part, which is unsorted. - Moreover, all elements in the second part are larger than all those in the first part
Selection sort concept
Selection sort concept
- Selection sort works by repeatedly selecting the smallest element from the unsorted part and adding it to the top of the sorted part.
Selection sort algorithm
Selection sort algorithm
Asymptotic analysis of the selection sort
- What is the complexity of selection sort?
- The main body consists of two nested loops
- We know how to analyze nested loops
O($n^2$) Selection sort
- Inside the inner loop we do O(1) work
- Line 3 - 7 covers $$\sum_{j = i+1}^{n} 1 = n - (i + 1)$$
- Line 1 - 9 covers $$\sum_{i = 1}^{n-1} n -(i+1) = n(n-1) - \frac{n(n-1)}{2} - n$$
- So selection sort is an O($n^2$) algorithm
- We know such algorithms are usable for up to about a million items
Insertion sort concept

The insertion sort algorithm also maintains the invariant that the first part of the sequence is sorted.
But this time we insert the next unsorted element rather than the smallest unsorted element.
Insertion sort concept
Insertion sort algorithm
Insertion sort example

O($n^2$) Inserion sort
- Inside the inner loop line 5 - 6, we do O(1) work
- The worst step for line 4 - 7 is $i - 1$
- The worst for line 1 - 9 is $$\sum_{i = 2}^{n} i - 1 = \frac{n(n-1)}{2}$$
- So the insertion sort is an O($n^2$) algorithm
- Q:When does the worst case occur?
- Q:When does the best case occur? What is the complexity in that case?
- Q:What happens in general?
Asymptotic analysis of the insertion sort
- We don't know in advance how many times this loop will iterate:4 - 7?
- A:The worst case occurs when the element to be inserted is smaller than all elements sorted so far. In this case, the loop will executed $i-1$ times: $$\sum_{i = 2}^{n} i-1 = \frac{n(n-1)}{2}$$
- A:So the worst case occurs when the list is in a reverse order.
- In this case, each iteration requires shuffling all elements down the sorted part.
Asymptotic analysis of the insertion sort
- A:The best case occurs when the list is already sorted.
- In this case, the inner loop just take O(1). So the insertion sort takes O($n$)
- It is also good on a partially sorted sequence.
- In practice, it is more efficient than other simple quadratic sort algorithms.
Divide-and-conquer sorting
- Q:Try to think about sorting in terms of divide-and-conquer. Express sorting as a divide-and-conquer algorithm in the way that seems most natural to you.
- A:Here's one answer which seems natural:
Split the input sequence into two halves. Recursively sort each of those halves and then merge the two sorted halves into one. - This is merge sort.
- An elegant idea which is easy to express, but is it efficient?
Merge sort algorithm
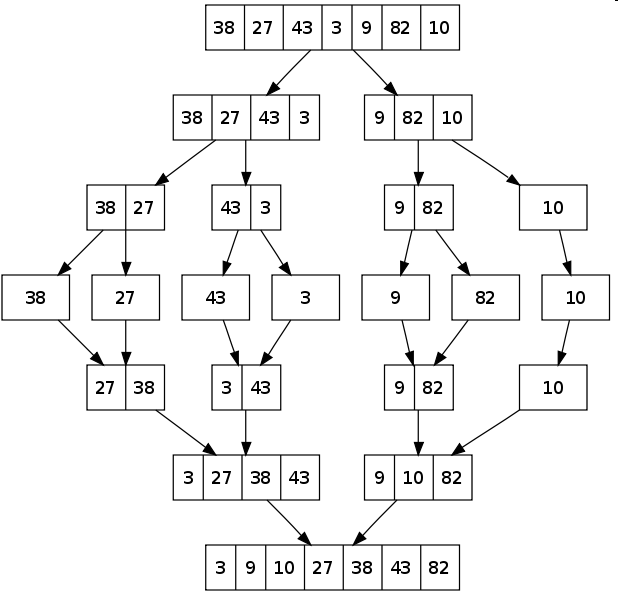
Merge sort example
Merge sort analysis
- To calculate the complexity of merge sort, we need to answer two questions:
1. What is the complexity of the merge subroutine?
2. What is the solution to the recurrence relation resulting from the recursive call?
Merge two sorted lists
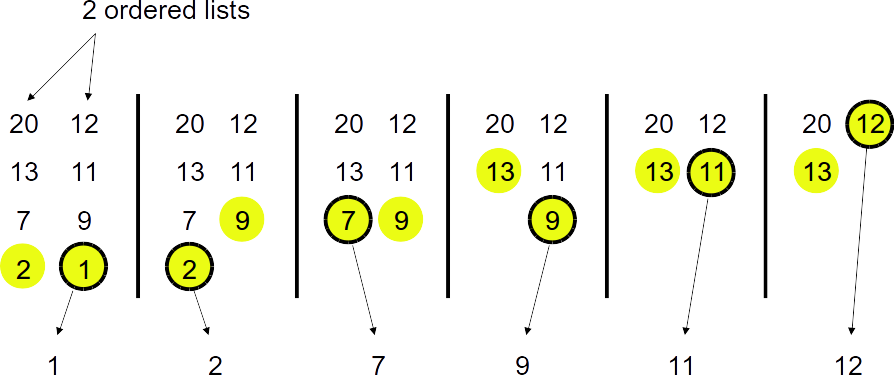
Strategy: examine front of both lists, repeatedly remove smallest.
Q: How many comparisons? Complexity of merging?
$n$ steps for total of $n$ elements
Merge sort analysis
- Line 1 - 3 covers O(1)
- Line 6 merges two sorted lists take $\theta(n)$
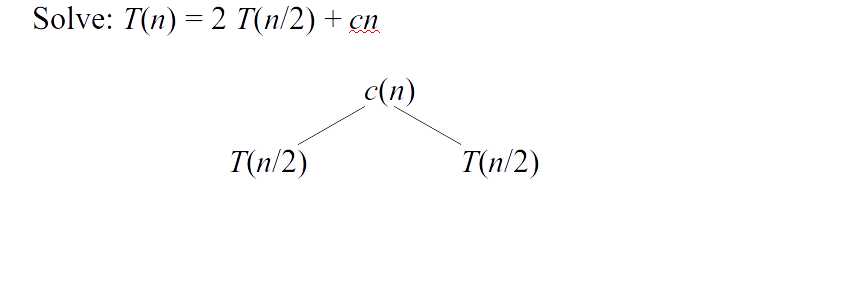
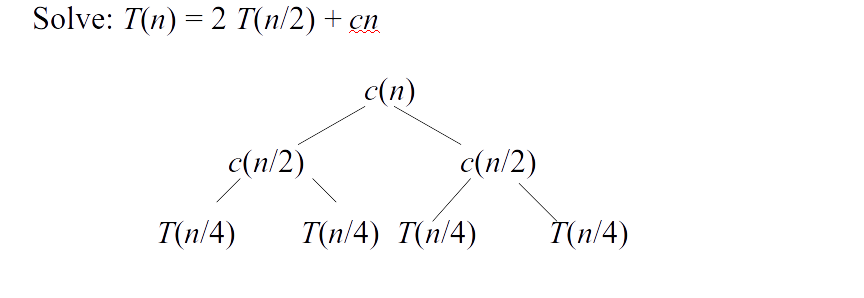
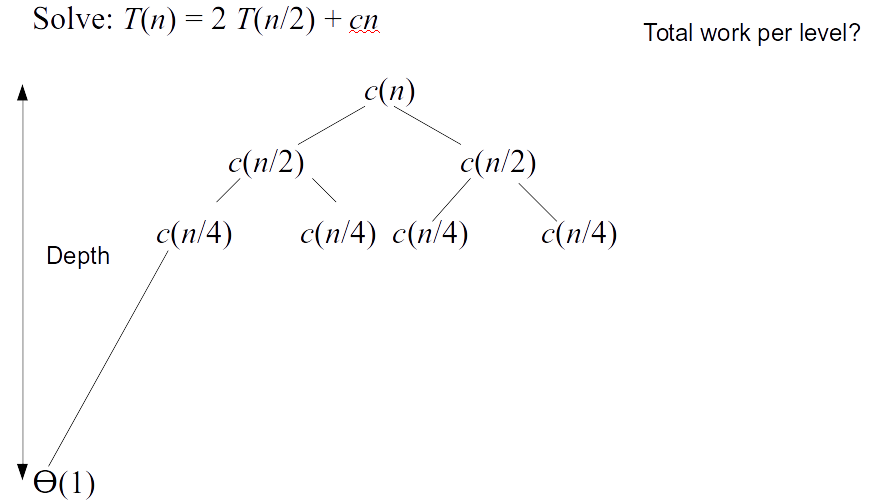
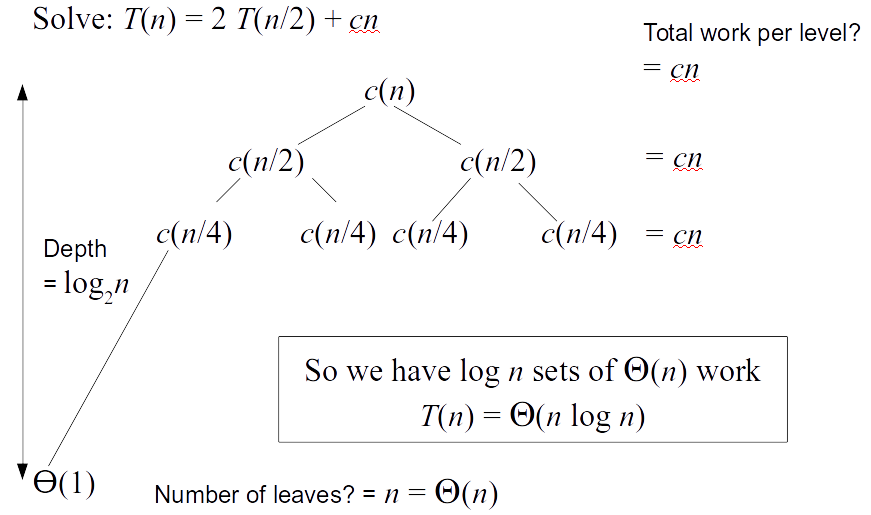
- Suppose $T(n)$ is the worst running time for $n$ elements \[T(n) = \left\{\begin{array}{ll} \theta(1) & \mbox{ if } n = 1 \\ 2 T(n/2) + \theta(n) & \mbox{ if } n > 1 \end{array}\right.\]
Merge sort analysis
Merge sort analysis
Merge sort analysis
Merge sort analysis
Merge sort analysis
Merge sort vs Quadratic sort
- Conclusion:Merge sort is o($n \log n$)
- Merge sort asymptotically beats insertion sort or selection sort
- In practice, merge sort is more efficient than insertion sort approx. when $n > 30$
- Obvious question:can we do any better?
- Is there a sorting algorithm that is o($n \log n$)?
Limits of Comparison-based sorting
- Think about the algorithms so far. The only way they learn anything about the sequence is by comparing elements.
- The number of comparisons required to put a set of elements in order is:
\[\Omega(n \log n)\]
So if our algorithm performs comparisons we can do no better - Q: Do we have to perform comparisons?
Dutch National Flag
Dutch National Flag
- The algorithm to solve this maintains the following invariant
- Algorithm sketch for $n$ element sequence:
1. Initialize r=1, w=1, b=n+1
2. Repeatedly perform the following until w=b:
If A[w] = red, swap(A[r], A[w]) and increment r and w
If A[w] = white, increment w
If A[w] = blue, swap(A[w], A[b-1]), decrement b
Dutch National Flag
- Q: Do you believe this algorithm sorts the flag?
- Q:What is the complexity?
- For each iteration of the loop, we either increment w or decrement b, bringing us one step closer to our termination criteria: w=b
- The algorithm is therefore linear in $n$
- We appear to have just seen a $\theta(n)$ sorting algorithm!
Dutch National Flag
- We appear to have just seen a $\theta(n)$ sorting algorithm!
- Q: Any explanation?
- A:If we know where to put elements by just looking at them, we can sort them in linear time.
- Similar idea can be used to any number of potential elements, putting them into “buckets” according to their value
- We must know the potential values beforehand
Conclusion
- We’ve seen some important sorting algorithms:
- Selection sort and insertion sort (asymptotically quadratic – with insertion sort being better in practice)
- Merge sort – an elegant application of divide and conquer giving us an O($n \log n$) sorting algorithm
- But we've seen when we know in advance what values we might get, we can have linear performance
Comments and Suggestions
- Assistant Professor Krung Sinapiromsaran
- Web: http://pioneer.netserv.chula.ac.th/~skrung
- Email: Krung.S@chula.ac.th