ขั้นตอนวิธีประเภทแบ่งเพื่อเอาชนะ (Divide-and-conquer algorithm)
เป็นขั้นตอนวิธีการแก้ปัญหาที่ใช้หลักการแบ่งปัญหาออกเป็นส่วนเล็ก ๆ แล้วทำการแก้ปัญหาในส่วนเล็ก ๆ นั้น
โดยไม่ขึ้นต่อกัน หลังจากนั้นจึงนำคำตอบที่ได้จากปัญหาย่อยเหล่านั้นมารวมกัน โดยปกติขนาดของข้อมูลที่ถูกแบ่งจะมีขนาดเล็กลง จนถึงระดับหนึ่ง
แล้วเราจึงทำการแก้ปัญหาขนาดเล็กนั้น โดยไม่ใช้การเรียกซ้ำ
ตัวอย่างของปัญหาที่สามารถใช้ขั้นตอนวิธีนี้คือ
- การคูณจำนวนขนาดใหญ่
- การค้นหาแบบทวิภาค
- การจัดเรียงข้อมูลแบบ Merge sort และ Quick sort
- การคูณกันของเมทริกซ์จัตุรัส สองเมทริกซ์
ปัญหาการคูณจำนวนขนาดใหญ่
กำหนดจำนวนสองจำนวนที่มีขนาดใหญ่ โดยปกติแล้วเราสามารถคูณตัวเลขหนึ่งหลักกับตัวเลขหลายหลักได้โดยง่าย
และเราทราบว่าการบวกกันของตัวเลขหลายจำนวนใช้เวลาที่น้อยมาก เราควรสร้างขั้นตอนวิธีในการคูณจำนวนเต็มบวกสองจำนวน 981 กับ 1234
อย่างไรถึงจะใช้จำนวนในการคูณของตัวเลขหนึ่งหลักที่น้อยที่สุด
วิธีการคูณแบบปกติ
หลักการคือ เลือกจำนวนที่มีค่ามากกว่าเป็นตัวตั้ง แล้วทำการหยิบเลขทีละตัวจากอีกจำนวนหนึ่งคูณจำนวนตั้งนั้น แล้วจึงทำการบวกกัน
ตัวอย่างจงหาผลคูณของ 981 กับ 1234
LONG_MULTI(m, n)
ข้อมูลเข้า m, n เป็นจำนวนที่ต้องการคูณกัน
ข้อมูลออก result เป็นผลคูณที่ได้
1. If m < n
2. then swap m and n
3. endif
4. set A[1,..,k] be the number for each digit of n where A[1] is the rightmost digit and A[k] is the leftmost digit
5. result = 0;
6. for i = 1 to k
7. result = result*10;
8. result = result + A[i]*m
9. endfor
10. return result
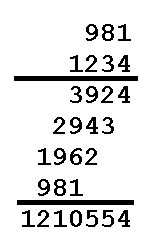
วิธีการคูณโดยการหารสองและคูณสอง
หลักการคือ กำหนดจำนวนหนึ่งเป็นตัวตั้ง เพื่อทำการคูณสองในแต่ละขั้น และตัวคูณซึ่งจะถูกหารสองในแต่ละขั้นจนเป็นศูนย์
แล้วจึงทำการบวกกันเฉพาะแถวของตัวตั้งที่หารแล้วเหลือเศษจากตัวคูณ ตัวอย่างจงหาผลคูณของ 981 กับ 1234
Russe(m, n)
ข้อมูลเข้า m, n เป็นจำนวนที่ต้องการคูณกัน
ข้อมูลออก result เป็นผลคูณที่ได้
1. result = 0
2. repeat
3. if m is odd
4. then result = result + n
5. m = m ÷ 2
6. n = n + n
7. until m < 1
8. return result
เมื่อ m ÷ 2 หมายถึง จำนวนเต็มที่ได้หลังจากนำ 2 ไปหาร m

วิธีการคูณโดย Divide-and-Conquer
หลักการคือการลดจำนวนของตัวเลขที่จะคูณโดยคูณเพียงครึ่งหนึ่งของจำนวนตัวเลขเดิม
MULTI_DC(m, n)
ข้อมูลเข้า m, n เป็นจำนวนที่ต้องการคูณกัน
ข้อมูลออก result เป็นผลคูณที่ได้
1. Make sure that m and n contains the number of digits in the power of two.
2. result = 0
3. if m or n has one digit
4. then result = m * n
5. return result
6. endif
7. Get the first half and the second half of m, m = m1 | m2 and mr = total number of digits in m2
8. Get the first half and the second half of n, n = n1 | n2 and nr = total number of digits in n2
9. result = result + DC(m1, n1) * 10mr + nr
10. result = result + DC(m1, n2) * 10mr
11. result = result + DC(m2, n1) * 10nr
12. result = result + DC(m2, n2)
13. return result
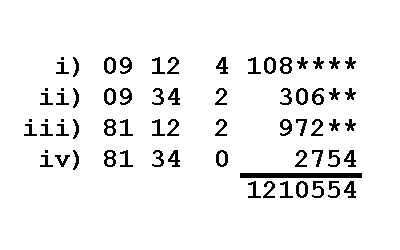
แบบฝึกหัด จงหาผลคูณต่อไปนี้โดยใช้ทั้งสามวิธี
- 9834 * 985
- 51823 * 3475
- 82837 * 87364
รูปทั่วไปของ Divide-and-conquer คือ
DIVIDE-AND-CONQUER(x)
ข้อมูลเข้า x เป็นข้อมูลเข้า
ข้อมูลออก y เป็นผลลัพธ์ที่ต้องการ
1. If x is sufficiently small or simple then
2. then return adhoc(x)
3. endif
4. For i = 1 to L do
5. yi = DC(xi)
6. recombine the yi's to obtain a solution y for x
7. endfor
8. return y
ปัญหาการค้นหาแบบทวิภาค (Binary search)
การค้นหาแบบนี้มักถูกใช้กับการค้นหาคำในพจนานุกรม เพราะว่า คำที่เก็บอยู่ในพจนานุกรมนั้นเรียงตามลำดับ
วิธีการหลักคือ การทดสอบกับคำที่อยู่กึ่งกลางของข้อมูล แล้วเทียบว่าเจอคำนั้นหรือไม่ ถ้าเจอให้หยุดมิฉะนั้น เราจะตัดสินใจในการเลือกข้างของ
ข้อมูลที่คำที่ต้องการค้นนั้นอยู่ โดยทิ้งข้อมูลอีกข้างที่คำนั้นไม่อยู่แน่นอน
เราอาจพิจารณาการค้นเชิงเส้นแบบง่าย ๆ คือ
SEQUENTIAL(T, x)
ข้อมูลเข้า T เป็นข้อมูลแบบแถวลำดับที่จะถูกค้น และ x คือคำที่ต้องการค้นใน T
ข้อมูลออก t เป็นดรรชนีใน T ที่บ่งบอกค่า x ถ้า x ไม่อยู่ใน T เราจะให้ t = -1
1. For t = 1 to length(T)
2. if( T[t] == x ) then return t
3. endfor
4. return t = -1;
BINSEARCH(T, x)
ข้อมูลเข้า T เป็นข้อมูลแบบแถวลำดับที่จะถูกค้นโดยข้อมูลมีการเรียงตามลำดับ และ x คือคำที่ต้องการค้นใน T
ข้อมูลออก t เป็นดรรชนีใน T ที่บ่งบอกค่า x ถ้า x ไม่อยู่ใน T เราจะให้ t = -1
1. n = length(T)
2. If n = 0 or x > T[n]
3. then return -1
4. else return BINREC(T, 1, n, x)
5. endif
BINREC(T, i, j, x)
ข้อมูลเข้า T เป็นข้อมูลแบบแถวลำดับที่จะถูกค้น, i และ j คือดรรชนีของ T และ x คือคำที่ต้องการค้นใน T โดยที่
T[i-1] < x  T[j] T[j]
ข้อมูลออก t เป็นดรรชนีใน T ที่บ่งบอกค่า x ถ้า x ไม่อยู่ใน T เราจะให้ t = -1
1. If i = j
2. then if(x = T[i]) then return i
3. else return -1
4. endif
5. endif
6. k = (i+j)÷ 2
7. if x  T[k]
8. then BINREC(T, i, k, x)
9. else BINREC(T, k+1, j, x)
10. endif T[k]
8. then BINREC(T, i, k, x)
9. else BINREC(T, k+1, j, x)
10. endif
หรือเราสามารถเขียน การค้นหาแบบทวิภาค โดยใช้การวนซ้ำดังนี้
BINITER(T, x)
ข้อมูลเข้า T เป็นข้อมูลแบบแถวลำดับที่จะถูกค้น และ x คือคำที่ต้องการค้นใน T
ข้อมูลออก t เป็นดรรชนีใน T ที่บ่งบอกค่า x ถ้า x ไม่อยู่ใน T เราจะให้ t = -1
1. n = length(T)
2. if (x > T[n]) then return -1
3. i = 1; j = n
4. while i < j do {
5. k = (i + j) ÷ 2
6. if (x  T[k]) then
7. then j = k;
8. else i = k+1
9. endwhile
10. if (x != T[i]) then return -1
11. return i T[k]) then
7. then j = k;
8. else i = k+1
9. endwhile
10. if (x != T[i]) then return -1
11. return i
การจัดลำดับข้อมูลแบบ Merge sort และ Quick sort
การจัดลำดับข้อมูลทั้งสองแบบใช้หลักการของการแบ่งเพื่อเอาชนะ เพราะว่า เราจะแบ่งรายการของสมาชิกออกเป็นสองส่วน
หลังจากจัดลำดับเรียบร้อยแล้ว เราอาจนำมารวมกัน เพื่อให้ได้คำตอบของการจัดเรียงทุกข้อมูล
ปัญหาการคูณเมทริกซ์ (Matrix multiplication)
กำหนดให้ A และ B เป็นเมทริกซ์ขนาด n × n และ C เป็นเมทริกซ์ของผลคูณซึ่งนิยามว่า
- Ci j =
 Ai k Bk j. Ai k Bk j.
เราได้ว่าแต่ละค่าของ Ci j จะใช้เวลา O(n) ถ้าเราสมมติว่าการคูณและการบวกตัวเลขเป็น elementary operations แต่เรามีค่าของ Ci j
อยู่ n2 ดังนั้นโดยการใช้นิยาม เราสามารถคำนวณเมทริกซ์ C โดย O(n3)
ปลายปี 1960s Strassen พบว่า เราสามารถลดจำนวนการคูณกันของตัวเลขในการคำนวณเมทริกซ์ผลคูณได้โดยใช้หลักการ divide-and-conquer
โดยเริ่มต้นเราจะแสดงว่า การคูณกันของเมทริกซ์ขนาด 2 × 2 ใช้จำนวนการคูณน้อยกว่า 8 คือ
- A =
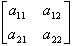 และ B = และ B = 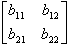
พิจารณาการคำนวณของตัวเลขเจ็ดตัวนี้
- m1 = (a2 1 + a2 2 - a1 1) (b2 2 - b1 2 + b1 1)
- m2 = a1 1 b1 1
- m3 = a1 2 b2 1
- m4 = (a1 1 - a2 1) (b2 2 - b1 2)
- m5 = (a2 1 + a2 2) (b1 2 - b1 1)
- m6 = (a1 2 - a2 1 + a1 1 - a2 2) b2 2
- m7 = a2 2 (b1 1 + b2 2 - b1 2 - b2 1)
เราพบว่าเราเพียงใช้การคูณเพียงเจ็ดครั้ง ซึ่งคำนวณ C ได้ดังนี้
- C =
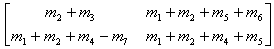
|