หลักการกำหนดการพลวัต Dynamic Programming
ปกติเราใช้หลักการพลวัต (Dynamic programming) ในการแก้ปัญหา Optimization โดยมีลักษณะคล้ายกับ Divide-and-conquer
ที่แบ่งปัญหาออกเป็นส่วนย่อย ๆ แล้วนำผลลัพธ์ของปัญหาย่อยเหล่านั้นมาแก้ปัญหาใหญ่ แต่สำหรับปัญหาย่อยที่การคำนวณนั้นไม่ขึ้นแก่กัน เราจะใช้
หลักการแบ่งเพื่อเอาชนะช่วยได้ แต่ถ้าการแก้ปัญหาย่อยเหล่านั้นขึ้นต่อกัน เรามักใช้หลักการพลวัตในการแก้ปัญหา
ถ้าเราพิจารณาต้นไม้ของการแก้ปัญหา เราจะพบว่าการแก้ปัญหาแบบแบ่งเพื่อเอาชนะเป็นการแก้ปัญหาจากบนลงล่าง (Top-down approach)
นั่นคือเราแก้ปัญหาขนาดใหญ่โดยการแบ่งย่อยเป็นปัญหาขนาดเล็ก ในขณะที่วิธีการพลวัตจะแก้ปัญหาจากล่างขึ้นบน (Bottom-up approach)
ซึ่งโดยทั่วไปเราจะเริ่มแก้ปัญหาขนาดเล็กก่อนแล้วจึงมารวมกันจนกระทั่งได้คำตอบของปัญหาจริง
การเขียนขั้นตอนวิธีการแก้ปัญหาแบบกำหนดการพลวัต ส่วนใหญ่ใช้หลักการดังนี้
- กำหนดลักษณะของโครงสร้างของผลเฉลยที่เหมาะที่สุด
- นิยามความสัมพันธ์เวียนเกิดของผลเฉลยที่เหมาะที่สุด
- คำนวณค่าโดยใช้วิธีการจากล่างขึ้นบน (Bottom-up approach)
- สร้างคำตอบจากค่าที่คำนวณได้
การคำนวณค่า Binomial coefficient
เราทราบว่า เราสามารถคำนวณค่าสัมประสิทธิของการกระจายได้จากสูตร
 = 1 ถ้า k = 0 หรือ k = n = 1 ถ้า k = 0 หรือ k = n = = 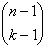 + +
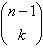 ถ้า 0 < k < n ถ้า 0 < k < n
ในกรณีที่เราทราบว่า 0  k k  n เราคำนวณค่า n เราคำนวณค่า
 ได้โดยใช้ขั้นตอนวิธีนี้ ได้โดยใช้ขั้นตอนวิธีนี้
C(n, k)
ข้อมูลเข้า n เป็นจำนวนเต็มบวก และ k แทนจำนวนเต็มที่ไม่น้อยกว่าศูนย์และไม่มากกว่า n
ข้อมูลออก ผลลัพธ์ที่ได้จาก 
1. if k == 0 or k == n then return 1
2. return C(n-1, k-1) + C(n-1, k)
เราพบว่าขั้นตอนวิธีที่เสนอมาข้างต้นจะมีการคำนวณค่าของ C(i, j) เมื่อ i < n, j < k ซ้ำๆ กันหลายครั้ง เช่น
- ในการคำนวณ C(5, 3) = C(4, 2) + C(4, 3) ซึ่งจะต้องมีการคำนวณ C(3, 2) ทั้งสองกรณี และในทำนองเดียวกับค่า C(2, 2)
ซึ่งเราจะใช้เวลาในการคำนวณอย่างน้อยคือ
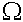 ( ( ) )
แต่ถ้าเราใช้วิธีการคิดแบบ Pascal's triangle เราสามารถคำนวณค่า C(n, k) ได้มีประสิทธิภาพดังตาราง
| | 0 | 1 |
2 | 3 | ... |
k - 1 | k |
|---|
| 0 | 1 | | | | | | |
|---|
| 1 | 1 | 1 | | | | | |
|---|
| 2 | 1 | 2 | 1 | | | | |
|---|
| 3 | 1 | 3 | 3 | 1 | | | |
|---|
| : | | | | | | | |
|---|
| n-1 | | | | | | C(n-1,k-1) |
C(n-1,k) |
|---|
| n | | | | | | | C(n,k) |
|---|
เราสามารถคำนวณ  แบบวนซ้ำได้ดังนี้ แบบวนซ้ำได้ดังนี้
IterativeC(n, k)
ข้อมูลเข้า n เป็นจำนวนเต็มบวก และ k แทนจำนวนเต็มที่ไม่น้อยกว่าศูนย์และไม่มากกว่า n
ข้อมูลออก ผลลัพธ์ที่ได้จาก 
1. Allocate table C of size n+1 by k+1 and set the default to be zero
2. for j = 0 to n
3. C(0, j) = 1;
4. endfor
5. for i = 1 to n
6. m = min{i, k}
6. for j = 1 to m
7. C(i, j) = C(i-1, j-1) + C(i-1, j);
8. endfor
9. endfor
10. return C(n, k)
การหาผู้ชนะในการแข่งทั้งรายการ World Series
พิจารณาการแข่งขันระหว่างสองทีม A และ B ซึ่งแข่งกันไม่เกิน 2n - 1 เกม โดยที่ผู้ชนะในการแข่งทั้งรายการคือทีมแรกที่ชนะ n
เกมก่อน สมมติว่าเราไม่มีการเล่นเสมอ และผลการเล่นในแต่ละครั้งไม่ขึ้นกับครั้งใด ๆ และ สำหรับการแข่งในแต่ละครั้งมีความน่าจะเป็นที่ A จะชนะคงที่
คือ p ดังนั้นความน่าจะเป็นที่ B จะชนะ q = 1 - p
กำหนดให้ P(i, j) แทนความน่าจะเป็นที่ทีม A จะชนะในการแข่งทั้งรายการเมื่อทีม A ต้องการชัยชนะอีก i ครั้ง ในขณะที่ทีม B ต้องการอีก j ครั้ง
ตัวอย่างเช่น ก่อนการแข่งขันเราได้ความน่าจะเป็นที่ทีม A จะชนะการแข่งทั้งรายการเท่ากับ P(n, n) หรือกล่าวอีกนัยหนึ่งคือทั้งสองทีมต้องการอีก n
เกมเพื่อชัยชนะทั้งรายการ
- ในกรณีที่ทีม A ไม่ต้องการชนะอีกแล้วคือ P(0, i) เราได้ว่าทีม A ชนะทั้งรายการเรียบร้อยแล้ว นั่นคือ P(0, i) = 1
- ในทำนองเดียวกัน ถ้าทีม B ไม่ต้องการชนะอีกแล้วคือ P(i, 0) เราถือว่าทีม A แพ้ในการแข่งทั้งรายการ นั่นคือ P(i, 0) = 0
และเราทราบว่าทีม A จะชนะในการแข่งด้วยความน่าจะเป็น p และแพ้ด้วยความน่าจะเป็น q ดังนั้น
- P(i, j) = p P(i-1, j) + q P(i, j-1), i
 1, j 1, j  1,
1,
เราสามารถเขียนขั้นตอนวิธีในการคำนวณค่า P(i, j) ได้ดังนี้
P(i, j)
ข้อมูลเข้า i เป็นจำนวนครั้งที่ทีม A ต้องการเอาชนะ และ j แทนจำนวนครั้งที่ทีม B ต้องการเอาชนะ เพื่อให้ชนะการแข่งทั้งรายการ
ข้อมูลออก ค่าของ P(i, j)
1. if i == 0 then return 1
2. if j == 0 then return 0
3. return P(i-1, j) + P(i, j-1)
กำหนดให้ T(k) แทนเวลาที่แย่ที่สุดในการคำนวณ P(i, j) เมื่อ k = i + j เราได้ว่า
- T(1) = c
- T(k)
 2 T(k - 1) + d, k > 1 2 T(k - 1) + d, k > 1
เราได้ว่า T(k)  2k(c/2 + d/2) - d 2k(c/2 + d/2) - d
ปัญหาลักษณะนี้จะคล้ายกับการคำนวณค่า  ในการคำนวณให้เร็วขึ้น
เราสามารถใช้หลักการเดียวกับ Binomial coefficient ในการคำนวณให้เร็วขึ้น
เราสามารถใช้หลักการเดียวกับ Binomial coefficient
series(n , p)
ข้อมูลเข้า n เป็นจำนวนครั้งที่แต่ละทีมต้องเอาชนะเพื่อชัยชนะของการแข่งขัน และ p แทนความน่าจะเป็นที่ทีม A จะชนะ
ข้อมูลออก ค่าของ P(n, n)
1. q = 1 - p
2. for s = 1 to n do
3. P(0, s) = 1; P(s, 0) = 0
4. for k = 1 to s - 1 do
5. p(k, s-k) = pP(k-1, s-k) + q P(k, s-k-1)
6. endfor
7. endfor
8. for s = 1 to n do
9. for k = 0 to n-s do
10. P(s+k, n-k) = p*P(s+k-1, n-k) + q*P(s+k, n-k-1)
11. endfor
12. endfor
13. return P(n, n)
ปัญหาการทอนเหรียญ Making Change (2)
จากปัญหาการทอนเหรียญที่น้อยที่สุดซึ่ง เราได้พิจารณาการแก้มาแล้วโดยใช้ Greedy algorithm เราพบว่าถ้าเรามีขนาดเหรียญ
บางประเภท เราไม่สามารถแก้ปัญหานี้โดยใช้ Greedy algorithm ได้ ตัวอย่างเช่น ถ้าเรามีเหรียญ 1, 4 และ 6 หน่วย การทอนเหรียญให้ผลรวมเป็น 8 หน่วย
โดยใช้ Greedy algorithm เราจะได้ว่าเราใช้ 3 เหรียญคือ 1 × 6 + 2 × 1 แต่ถ้าเราทอนเหรียญ 2 × 4 เราพบว่าเราใช้เพียงสองเหรียญเท่านั้น
เราแก้ปัญหานี้โดยใช้ Dynamic programming โดยทำการสร้างตารางการทอนของค่าที่ เพิ่มขึ้นเรื่อย ๆ จากค่าในตารางที่ได้คำนวณมาแล้ว
- กำหนดให้ i แทนค่าของเหรียญ 1 แบบที่สามารถใช้ทอนได้ (แทนแถวที่ i) เรียก di ซึ่งมากกว่า 0
และ
กำหนดให้ N แทนค่าที่ต้องทอน
เราจะสร้างตารางของ c(1..n, 0..N) โดยที่ c(i, j) หมายถึง จำนวนเหรียญที่ทอนที่น้อยที่สุดสำหรับค่า j, 1
 j j  N โดยใช้จำนวนเหรียญ 1, 2, ..., i
คำตอบที่ต้องการคือค่าของ c(n, N) N โดยใช้จำนวนเหรียญ 1, 2, ..., i
คำตอบที่ต้องการคือค่าของ c(n, N)
ในการเติมค่าในตาราง เราเริ่มจาก c(i, 0) = 0 ทุก i = 1, 2, ..., n เพราะเราไม่มีความจำเป็นต้องทอนเหรียญใด ๆ
ในการทอนเหรียญ เราอาจไม่จำเป็นต้องทอนเหรียญที่มีค่า di เลย นั่นคือ c(i, j) = c(i-1, j)
หรือ เราอาจเลือกทอนหนึ่งเหรียญของ di ทำให้ได้ว่า c(i, j) = 1 + c(i, j - di) เนื่องจากเราต้องการหาจำนวนเหรียญที่น้อยที่สุด
- c(i, j) = min{c(i-1, j), 1 + c(i, j - di)}
สำหรับในกรณีที่ i < 1 หรือ j < di เราพบว่าค่าหนึ่งในที่เลือกจะออกนอกตาราง เราจะกำหนดให้ค่านั้นเป็น
+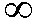 เพื่อไม่ให้เกิดการเลือกใช้ เพื่อไม่ให้เกิดการเลือกใช้
ในตารางที่ให้เป็นการแก้ปัญหาการทอนเหรียญ สามประเภทคือ 1, 4, 6 โดยจำนวนที่ต้องทอนคือ 8
| เหรียญ\ค่าที่ต้องทอน | 0 |
1 | 2 |
3 | 4 | 5 |
6 | 7 | 8
|
|---|
| d1 = 1 | 0 | 1 | 2 |
3 | 4 | 5 | 6 |
7 | 8 |
|---|
| d2 = 4 | 0 | 1 | 2 |
3 | 1 | 2 | 3 |
4 | 2 |
|---|
| d3 = 6 | 0 | 1 | 2 |
3 | 1 | 2 | 1 |
2 | 2 |
|---|
โดยใช้ขั้นตอนวิธีดังนี้
coins(N)
ข้อมูลเข้า N เป็นจำนวนเต็มบวกหรือศูนย์
ข้อมูลออก จำนวนเหรียญที่ต้องทอนที่น้อยที่สุด
1. d(1, 2, 3) = (1, 4, 6);
2. for i = 1 to n do
3. c(i, 0) = 0
4. endfor
5. for i = 1 to n do
6. for j = 1 to N do
7. if i == 1 and j < d(i) then
8. c(i, j) = +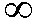 ;
9. else if i == 1 then
10. c(i, j) = 1 + c(1, j - d(1));
11. else if j < d(i) then
12. c(i, j) = c(i-1, j)
13. else
14. c(i, j) = min{c(i-1, j), 1+c(i, j-d(i))}
15. endif
16. endfor
17. endfor
18. return c(n, N) ;
9. else if i == 1 then
10. c(i, j) = 1 + c(1, j - d(1));
11. else if j < d(i) then
12. c(i, j) = c(i-1, j)
13. else
14. c(i, j) = min{c(i-1, j), 1+c(i, j-d(i))}
15. endif
16. endfor
17. endfor
18. return c(n, N)
การคูณต่อกันของเมทริกซ์ Matrix-chain multiplication
กำหนดชุดของเมทริกซ์ < A1, A2, A3, ..., An >
ซึ่งต้องการหาคำตอบ A1 × A2 × ... × An
เรากล่าวว่า ชุดของเมทริกซ์มีผลคูณของเมทริกซ์ซึ่ง fully parenthesized ถ้า ชุดของเมทริกซ์นั้นมีหนึ่งเมทริกซ์ หรือ
ชุดของเมทริกซ์นั้นประกอบด้วยผลคูณของ fully parenthesized เมทริกซ์ชุดย่อย ๆ โดยมีวงเล็บคล่อมไว้
ตัวอย่างเช่น ชุดของเมทริกซ์ < A1, A2, A3, A4 > จะมีผลคูณซึ่ง fully parenthesized
อยู่ 5 แบบคือ
- (A1 × (A2 × (A3 × A4))), (A1
× ((A2 × A3) × A4)), ((A1 × A2) ×
(A3 × A4)), ((A1 × (A2 × A3)) ×
A4), (((A1 × A2) × A3) × A4)
ในการคูณกันของเมทริกซ์เราจะพบว่าผลคูณของจำนวน scalar ในเมทริกซ์ และขนาดของเมทริกซ์มีผลต่อการวิเคราะห์ running time
MATRIX-MULTIPLY(A, B)
ข้อมูลเข้า A, B เป็นเมทริกซ์ขนาด p × q และ q × r ตามลำดับ
ข้อมูลออก C เป็นเมทริกซ์ผลคูณของ A × B ซึ่งมีขนาด p × r
1. if columns[A] != rows[B] then return error "incompatible multiplication"
2. for i = 1 to rows[A]
3. for j = 1 to columns[B] do
4. C[i, j] = 0
5. for k = 1 to columns[A]
6. C[i, j] = C[i, j] + A[i, k] * B[k, j]
7. endfor
8. endfor
9. endfor
10. return C
จำนวนการคูณกันของจำนวนตัวเลขสองจำนวน จะเป็นตัวกำหนด running time analysis ของการคูณเมทริกซ์
พิจารณาตัวอย่าง A1, A2, A3 มีขนาด 10 × 100, 100 × 5 และ 5 × 50 ตามลำดับ
ถ้าเราให้การคูณคือ ((A1 × A2) × A3) เราพบว่าเราต้องคูณกัน 10 × 100 × 5 = 5000
ในการคำนวณ A1 × A2 และอีก 10 × 5 × 50 = 2500 ในการคูณต่อด้วย A3
ผลคูณสุดท้ายรวมทั้งหมดเป็น 7500
แต่ถ้าเราคำนวณผลคูณดังนี้ (A1 × (A2 × A3)) เราจะได้ผลรวมของการคูณคือ 100 × 5
× 50 + 10 × 100 × 50 = 25000 + 50000 = 75000 ซึ่งสูงกว่าการคูณแบบแรกถึง 10 เท่า
ปัญหาการคูณต่อกันของเมทริกซ์ Matrix-chain multiplication problem
กำหนดชุดของเมทริกซ์ < A1, A2, A3, ..., An > ซึ่งมีมิติ
Ai = p[i-1] × p[i] เราต้องการหาการจัดชุดของเมทริกซ์แบบ fully parenthesized ที่มีจำนวนการคูณของ scalar ที่น้อยที่สุด
ถ้าเราคำนวณหาความเป็นไปได้ทั้งหมดในการใส่วงเล็บ เราจะได้ขั้นตอนวิธีที่มี running time เป็น O(2n)
กำหนดให้ T(n) เป็นจำนวนการใส่วงเล็บทั้งหมดที่เป็นไปได้ (โดยแต่ละแบบเกิดการคำนวณที่ต่างกัน)
เราสามารถเขียนสมการเวียนเกิดของปัญหานี้ได้ดังนี้
T(1) = 1, T(2) = 1, T(n) = 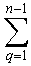 T(q) T(n - q) สำหรับ n > 1 T(q) T(n - q) สำหรับ n > 1
คำตอบของปัญหานี้คือลำดับที่เรียกว่า Catalan numbers ซึ่งมีคำตอบคือ T(n) = 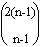 / n / n
การแก้ปัญหา Matrix-chain multiplication problem
เราแบ่งเป็นขั้น ๆ ได้ดังนี้
- กำหนด A(i..j) หมายถึงการคูณของ Ai × Ai+1 × ... × Aj ดังนั้น A(1..n)
สามารถคำนวณได้จากปัญหาย่อย ๆ คือ A(1..k) กับ A(k..n) ซึ่งเราพบว่าผลเฉลยที่เหมาะที่สุดจะเกิดจากการแก้ปัญหาย่อยเหล่านี้
โดยให้มีการคูณกันที่น้อยที่สุดด้วย
- เรานิยามความสัมพันธ์เวียนเกิดโดยให้ m[i,j] เป็นจำนวนผลคูณของ scalar product ที่น้อยที่สุดสำหรับการคำนวณ A(i..j)
จะได้
- m[i, i] = 0 และ m[i, j] = min{m[i, k] + m[k+1, j] + p(i-1) p(k) p(j) สำหรับ i < j }
เรากำหนด s[i, j] คือดัชนีที่ใช้ในการแยกผลคูณ A(i...k) × A(k+1...j) เพื่อใช้ในการกำหนดตำแหน่งการใส่วงเล็บ
- การแก้สมการเวียนเกิดนี้สามารถใช้หลักการหรือสูตรซึ่งได้ศึกษามาแล้ว
ในทางปฏิบัติแล้วเราสามารถเขียนขั้นตอนวิธีซึ่งสามารถหาคำตอบได้ในลักษณะของ polynomial ดังนี้
MATRIX-CHAIN-ORDER(p)
ข้อมูลเข้า p เป็นเวกเตอร์ของขนาดของเมทริกซ์
ข้อมูลออก m เป็นเมทริกซ์คำตอบของการคำนวณที่ใช้ผลคูณของ scalar ที่น้อยที่สุด
และ s เป็นเมทริกซ์ของคำตอบในการคูณ
1. n = length[p] - 1
2. for i = 1 to n
3. m[i, i] = 0
4. endfor
5. for a = 2 to n do
6. for i = 1 to n-a + 1
7. j = i+a - 1
8. m[i, j] = Infinity
9. for k = i to j - 1
10. q = m[i, k] + m[k+1, j] + p[i-1] p[k] p[j]
11. if q < m[i, j] then
12. (m[i, j], s[i, j]) = (q, k)
13. endif
14. endfor
15. endfor
16. endfor
17. return m and s
ตัวอย่างเช่นกำหนด
| Matrix | Dimension |
|---|
| A1 | 30 × 35 |
| A2 | 35 × 15 |
| A3 | 15 × 5 |
| A4 | 5 × 10 |
| A5 | 10 × 20 |
| A6 | 20 × 25 |
เราสามารถสร้างตารางคำตอบได้ดังนี้
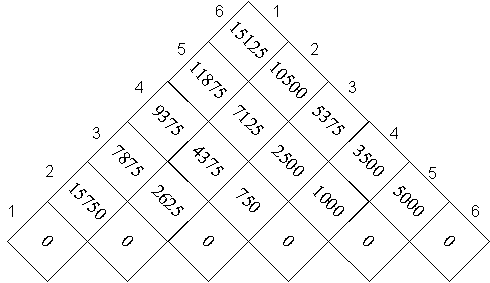
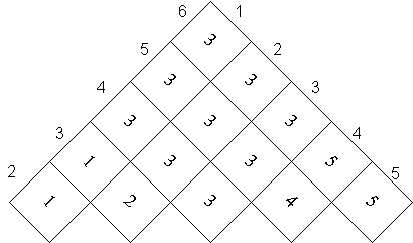
นั่นคือคำตอบของ m[1, 6] คือ 15125 และคำตอบของ m[2,5] คือค่าต่ำสุดของชุดตัวเลขดังต่อไปนี้
- m[2, 2] + m[3, 5] + p[1]p[2]p[5] = 13000
- m[2, 3] + m[4, 5] + p[1]p[3]p[5] = 7125
- m[2, 4] + m[5, 5] + p[1]p[4]p[5] = 11375
- เราจะพบว่าคำตอบที่ได้ เพียงกำหนดลำดับการคูณกันของเมทริกซ์ ซึ่งถ้าเราต้องการคำนวณการคูณเราสามารถเขียนขั้นตอนวิธีดังนี้
MATRIX-CHAIN-MULTIPLY(A, s, i, j)
ข้อมูลเข้า A ชุดของเมทริกซ์ A1, ..., An, s เป็นเมทริกซ์คำตอบของ
MATRIX-CHAIN-ORDER(p), i เป็นดัชนีเริ่มต้นและ j เป็นดัชนีสุดท้าย
ข้อมูลออก B เป็นเมทริกซ์คำตอบของการคูณ Ai × ... × Aj
1. if j > i then
2. X = MATRIX-CHAIN-MULTIPLY(A, s, i, s[i, j])
3. Y = MATRIX-CHAIN-MULTIPLY(A, s, s[i, j]+1, j)
4. return MATRIX-MULTIPLY(X, Y)
5. endif
6. return Ai
|