Heuristic
ในบางครั้งการทราบว่าปัญหาที่เราเผชิญอยู่นั้นยากในการแก้ เราอาจต้องการหาเพียงวิธีการที่สามารถหาผลเฉลยหรือคำตอบ
ที่ยอมรับได้ โดยอาจไม่ใช่วิธีที่ดีที่สุดจริง หรือแม้แต่คำตอบอาจไม่ตอบคำถามที่ต้องการอย่างแท้จริง
คำว่า Heuristic algorithm หรือ Heuristic ในที่นี้เราหมายถึง วิธีการหรือขั้นตอนวิธีที่สามารถหาคำตอบที่ดี หรืออาจได้
คำตอบที่เหมาะสมที่สุดในกรณีที่เราโชคดี หรือในบางครั้งอาจไม่ได้คำตอบที่ดี หรือเหมาะที่สุด ในกรณีที่โชคร้าย Heuristic อาจมีทั้งแบบ
deterministic หรือ probabilistic
การระบายสีของกราฟ
กำหนดกราฟไม่มีทิศทาง G = (V, E) เราต้องการระบายสีจุดยอดของ V โดยบังคับว่าสำหรับจุดยอดที่ติดกัน (adjacent)
ต้องไม่มีสีที่เหมือนกัน ปัญหาคือเราต้องการทราบจำนวนสีน้อยที่สุดที่ต้องการใช้ ค่าต่ำสุดนี้เราเรียกว่า chromatic number ของกราฟ
ตัวอย่างเช่นกราฟข้างล่าง G เราสามารถใช้สองสีในการระบายได้ แต่ H เราต้องใช้สามสี
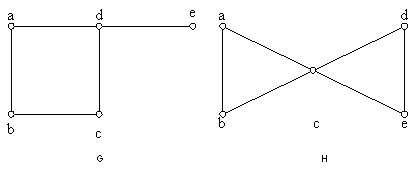
เราพบว่าปัญหาในการหาจำนวนสีในการระบายที่น้อยที่สุดเป็นปัญหา NP-hard
วิธีหนึ่งที่เรานำมาใช้ในการแก้ปัญหานี้คือ การใช้ greedy heuristic
Color_greedy(G)
ข้อมูลเข้า G แทนกราฟไม่มีทิศทาง
ข้อมูลออก การระบายสีและจำนวนสีที่ใช้
1. Set k = 0
2. while all vertices in G have not been colored
3. Choose the new color k+1
4 For each v in G
5 If v is not a neighbours of last painted k-1
6 then painted v using k
7 endif
8 endfor
9 endwhile
นั่นคือ เราเริ่มจากเลือกสีแรก แล้วทำการระบายให้กับจุดยอดให้มากที่สุด เท่าที่จะมากได้ แล้วเราค่อยทำการเลือกสีใหม่ แล้วทำซ้ำอย่างนี้ไปเรื่อย ๆ
เราจะได้ว่าวิธีการนี้บางครั้งให้คำตอบที่ดีที่สุด บางครั้งไม่ใช่ ตัวอย่างเช่น
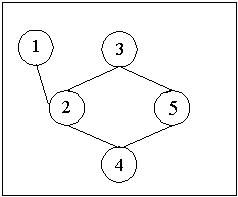ถ้าเราระบายสีโดยใช้ Color_greedy(G) ตามลำดับของจุดยอด 1, 2, 3, 4, 5 เราจะได้คำตอบที่ดีที่สุดคือ 2 สี
แต่ถ้าเราระบายสีตามลำดับของจุดยอด 1, 5, 2, 3, 4 เราจะได้คำตอบที่ต่างออกไปและไม่เป็นคำตอบที่ดีที่สุด
เราสามารถแสดงได้ว่า สำหรับกราฟ G ใด ๆ จะมีลำดับของจุดยอดที่ทำให้ขั้นตอนวิธี Color_greedy หาคำตอบที่ดีที่สุดได้
ดังนั้น เราอาจหวังได้ว่าสำหรับกราฟรูปใด ๆ เราอาจโชคดีสามารถหาคำตอบที่ดีที่สุดตามที่ต้องการได้
- การพิสูจน์ เราสมมติว่า G เป็นกราฟซึ่งต้องการจำนวนสีที่น้อยที่สุดคือ k
- สมมติว่าเรามีผู้วิเศษคนหนึ่งบอกว่า วิธีการระบายสีโดยใช้ k สีให้เราทราบ
- เราสามารถทราบลำดับของจุดยอดที่จะทำให้ขั้นตอนวิธี Color_greedy ได้คำตอบที่ดีที่สุด
- เราทำการเลือกสีแรก แล้วนำจุดยอดทั้งหมดที่ใช้สีแรก มากำหนดเป็นลำดับแรก เลือกสีที่สองและกำหนดจุดยอดให้เรียงต่อไป
อย่างนี้เรื่อย ๆ เราจะได้ลำดับของจุดยอดที่ต้องการ
- ถ้าเราใช้ขั้นตอนวิธี Color_greedy กับลำดับนี้เราจะพบว่า Color_greedy จะให้จำนวนสีเท่ากับ k ตามที่ต้องการ
แต่เราก็พบว่า เราสามารถสร้างกราฟ ที่ทำให้ขั้นตอนวิธีนี้แย่ที่สุดเท่าที่เราต้องการ นั่นคือ เราสามารถสร้างกราฟที่ใช้สีเพียง k สี แต่ถ้าเราใช้ขั้นตอนวิธี
Color_greedy จะใช้ c สี โดยที่ c/k จะมีขนาดใหญ่เท่าไหร่ก็ได้
- วิธีการพิสูจน์นี้คือ เราสามารถสร้างกราฟ G ที่มีจุดยอด 2 n โดยที่เราให้จุดยอดเหล่านั้นเรียงลำดับ 1, 2, 3, ..., 2 n
- เราจะสร้างด้านเชื่อมระหว่าง จุดยอดที่เป็นเลขคี่กับทุกจุดยอดที่เป็นเลขคู่ และทำลักษณะนี้ในทำนองเดียวกับจุดยอดที่เป็นเลขคู่
เราจะได้ bipartite กราฟ ซึ่งจุดยอดสามารถแบ่งออกเป็นสองเซต N1 กับ N2
- กราฟนี้สามารถระบาย โดยใช้เพียงสองสีเท่านั้น
- สำหรับขั้นตอนวิธี Color_greedy เมื่อใช้กับลำดับ 1, 2, 3, ..., 2 n เราพบว่า เราต้องใช้ สีทั้งหมด n สี
- นั่นคือเราสามารถ สร้างกราฟที่ทำให้จำนวนสีที่ต้องใช้มีจำนวนมาก ตามที่ต้องการได้
การหาเส้นทางเดินของคนขายของ (Traveling Salesperson)
กำหนดเมือง 1, 2, ..., n เมืองที่เราทราบระยะทางระหว่างสองเมืองใด ๆ คนขายของต้องการเดินทางจากเมืองหนึ่งไปอีก
เมืองหนึ่งจนครบทุกเมือง เพียงครั้งเดียว แล้วย้อนกลับมาเมืองเริ่มต้น โดยให้มีระยะทางในการเดินทั้งหมดสั้นที่สุด กำหนดว่าระยะทางทั้งหมดไม่เป็น
จำนวนลบ
เราพบว่าปัญหานี้เป็นปัญหา NP-hard และขั้นตอนวิธีที่หาผลเฉลยนั้นยังไม่สามารถใช้ได้กับปัญหาที่มี n ขนาดใหญ่
ถ้าเรากำหนดให้แต่ละเมืองเขียนแทนด้วยจุดยอด และระยะทางระหว่างเมืองคือน้ำหนักของด้านระหว่างจุดยอดนั้น เราพบว่าปัญหา TSP คือการหา
Hamiltonian cycle ที่มีผลรวมของน้ำหนักต่ำที่สุด
ตัวอย่างเช่น เรามีเมืองหกเมืองที่มีระยะดังนี้
| From |
To | 2 | 3
| 4 | 5
| 6 |
|---|
| 1 |
| 3 | 10
| 11 | 7
| 25 |
|---|
| 2 |
| | 8
| 12 | 9
| 26 |
|---|
| 3 |
| |
| 9 | 4
| 20 |
|---|
| 4 |
| |
| | 5
| 15 |
|---|
| 5 |
| |
| |
| 18 |
|---|
เราได้เส้นทางเดินที่ต่ำที่สุดคือ 58 โดยเดินทางจาก 1 ไป 2 ไป 3 ไป 6 ไป 4 ไป 5 ไป 1
วิธี Greedy heuristic เราอาจกำหนดโดยให้เริ่มจากจุดยอดใด ๆ โดยในการเลือกเมืองถัดไป เราเลือกระยะทางที่สั้นที่สุดในขณะนั้นไปยังเมือง
ที่ยังไม่เคยไปมาก่อน
ถ้าเราใช้วิธีนี้กับตัวอย่างข้างต้นโดยเริ่มที่ 1 เราจะได้ทัวร์คือ 1, 2, 3, 5, 4, 6, 1 ซึ่งใช้ระยะทางทั้งหมด 60 ไม่ใช่คำตอบที่ดีที่สุด
แต่ค่าที่ได้ก็ไม่ห่างจากค่าที่ดีที่สุดมากนัก
|
ขั้นตอนวิธีประเภทศึกษาสำนึก Heuristic
