ขนาดของข้อมูลเข้าและค่าใช้จ่ายในการคำนวณ
สำหรับทฤษฎีทางตัวเลข เราจะจัดการกับตัวเลขเพียงหนึ่งหรือสองตัวซึ่งมีขนาดใหญ่ แทนที่จะมีจำนวนของตัวเลขหลายตัว
ดังนั้นขนาดของข้อมูลเข้ามีขนาดใหญ่ เราจะหมายถึงตัวเลขที่มีค่าใหญ่มาก นั่นคือเราจะวัดขนาดของตัวเลข โดยการนับจำนวนบิตในการแทนตัวเลขนั้น ๆ
เรากล่าวว่าขั้นตอนวิธีทางตัวเลขที่มี จำนวนเต็ม a1, ..., ak เป็น Polynomial time algorithm ถ้าขั้นตอนวิธีนั้นใช้เวลา
Polynomial time ในเทอมของ lg a1, ..., lg ak หรือ Polynomial time ที่ขึ้นกับความยาวของบิต
ที่แปลงเลขนั้นให้อยู่ในรูปเลขฐานสอง
ในที่นี้เราจะให้ elementary operation หรือ bit operation แทนด้วย การคำนวณทาง arithematic เช่น การคูณ การหารและการหาเศษของบิต
- ในการคิดวิธีนี้ เราได้ว่า การคูณของสองจำนวนเต็มที่มีขนาด m-bit โดยวิธีการตั้งคูณจะใช้ bit operation เท่ากับ
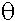 (m2) (m2)
- ในทำนองเดียวกัน การหารของสองจำนวนเต็มที่มีขนาด m-bit โดยวิธีปกติจะใช้ bit operation เท่ากับ
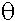 (m2) (m2)
- การหาเศษของสองจำนวนเต็มที่มีขนาด m-bit โดยวิธีปกติจะใช้ bit operation เท่ากับ
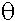 (m2) (m2)
- ปัจจุบันการคูณของสองจำนวนเต็มที่มีขนาด m-bit ที่เร็วที่สุดโดยใช้วิธีการ divide-and-conquer ใช้ bit operation เท่ากับ
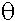 (mlg 3) (mlg 3)
พื้นฐานทางทฤษฎีตัวเลข
กำหนด 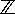 เป็นเซตของจำนวนเต็ม และ เป็นเซตของจำนวนเต็ม และ
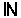 0 เป็นเซตของจำนวนเต็มบวกรวมศูนย์ 0 เป็นเซตของจำนวนเต็มบวกรวมศูนย์
นิยาม เรากล่าวว่า d หาร a (d divides a) เขียนแทนด้วย d | a หมายความว่า มีจำนวนเต็ม k บางตัวที่
a = d k
- จำนวนเต็มทุกตัวหารศูนย์
- ถ้า a > 0 และ d | a แล้ว | d |
 | a | | a |
- ถ้า d | a แล้วเรากล่าวว่า a เป็น multiple ของ d
- ถ้า d ไม่หาร a เราเขียนแทนด้วย d
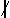 a a
- ถ้า d | a และ d
 0 เรากล่าวว่า d เป็นตัวหารของ a (d เป็น divisor ของ a) 0 เรากล่าวว่า d เป็นตัวหารของ a (d เป็น divisor ของ a)
- d | a ก็ต่อเมื่อ -d | a
จากความรู้สุดท้าย เราอาจละไม่สนใจจำนวนเต็มที่เป็นลบได้ ดังนั้นต่อไปนี้เราจะสนใจตัวหารที่เป็นบวกเท่านั้น
สำหรับจำนวนเต็ม a ใด ๆ เราจะมี trivial divisors คือ 1 และ a สำหรับตัวหารที่ไม่ใช่ trivial divisor เราจะเรียกว่าเป็น factor ของ a
เช่น factor ของ 20 คือ 2, 4, 5, 10
นิยาม สำหรับจำนวนเต็มบวก p ใด ๆ ที่มากกว่า 1 ซึ่งมีตัวหารเพียงแค่สองตัวคือ 1 กับ p เรากล่าวว่า p เป็นจำนวนเฉพาะ
(prime) จำนวนเฉพาะได้แก่
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, ...
เราสามารถแสดงได้ว่า จำนวนเฉพาะมีจำนวนไม่จำกัด สำหรับจำนวนเต็มที่มากกว่า 1 ที่ไม่ใช่จำนวนเฉพาะ เราจะเรียกว่า จำนวนประกอบ (composite)
เช่น 39 เป็นจำนวนประกอบ เพราะ 3 | 39
เราเรียก 1 ว่าเป็น unit ซึ่งไม่ใช่จำนวนเฉพาะและจำนวนประกอบ และเรากล่าวว่า 0 และจำนวนเต็มลบไม่ใช่จำนวนเฉพาะและจำนวนประกอบ
นิยาม กำหนดจำนวนเต็มบวก n เราสามารถจำนวนเต็มออกเป็นส่วน ๆ ที่แยกกัน โดยที่เซตแรกเป็นจำนวนที่เป็น
multiple ของ n และอีกเซตเป็นจำนวนที่ไม่ใช่ แต่ในเรื่องของทฤษฎีจำนวน เราจะสนใจเซตของเศษเหลือที่ได้จากการหาร n
ทฤษฎีการหาร (Division theorem) สำหรับจำนวนเต็ม a และจำนวนเต็มบวก n เราได้ว่ามีจำนวนเต็ม q และ r
เพียงชุดเดียวเท่านั้นที่ทำให้ 0  r < n และ a = q n + r r < n และ a = q n + r
เราเรียกค่า q = 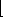 q/n q/n 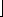 ว่า
ผลหาร (quotient) ของการหาร และค่า r = a mod n เป็นค่าเศษเหลือ (remainder) ของการหาร ว่า
ผลหาร (quotient) ของการหาร และค่า r = a mod n เป็นค่าเศษเหลือ (remainder) ของการหาร
- n | a ก็ต่อเมื่อ a mod n = 0
เรายังได้ว่า
- a =
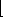 q/n q/n 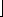 n + (a mod n) n + (a mod n)
- หรือ a mod n = a -
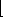 q/n q/n 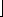 n n
เรานิยาม a  b (mod n) เมื่อ (a mod n) = (b mod n) หรือ a และ b มีเศษเหลือเท่ากันเมื่อหารด้วย n
เรากล่าวว่า a equivalent กับ b ใน modulo n b (mod n) เมื่อ (a mod n) = (b mod n) หรือ a และ b มีเศษเหลือเท่ากันเมื่อหารด้วย n
เรากล่าวว่า a equivalent กับ b ใน modulo n
- a
 b (mod n) ก็ต่อเมื่อ n | (b - a) b (mod n) ก็ต่อเมื่อ n | (b - a)
เช่น 61  6 (mod 11), -13 6 (mod 11), -13  22
(mod 5) 22
(mod 5)
เราจะได้ว่าเซตของจำนวนเต็มสามารถถูกแบ่งของเป็นเซตย่อย ๆ ที่ไม่มีสมาชิกร่วมกันได้ เรียกว่า equivalence class modulo n ซึ่งจะแบ่ง
ตามเศษเหลือที่ได้จากการหารตัวเลขนั้น ๆ ด้วย n
- [a]n = {a + kn | k
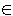 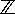 } }
เช่น [3]7 = {..., -11, -4, 3, 10, 17, ... }
กำหนด
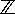 n = {[a]n | 0 n = {[a]n | 0  a
a  n-1} n-1}
เราได้ว่า 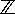 n = {0, 1, 2, ..., n-1} n = {0, 1, 2, ..., n-1}
นิยาม ถ้า d เป็นดัวหารของ a และ d เป็นตัวหารของ b เรากล่าวว่า d เป็นตัวหารร่วมของ a และ b เช่น
ตัวหารของ 30 คือ 1, 2, 3, 5, 6, 10, 15, 30 และตัวหารของ 24 คือ 1, 2, 3, 6, 12, 24 เราได้ว่าตัวหารร่วมของ 30 กับ 24 คือ 1, 2, 3, 6
สมบัติที่สำคัญอย่างหนึ่งของตัวหารร่วมคือ
- d | a และ d | b จะได้ว่า d | (a + b) และ d | (a - b)
หรือเขียนในรูปทั่วไปได้ว่า
- d | a และ d | b จะได้ว่า d | (ax + by) สำหรับทุกจำนวนเต็ม x, y
นอกจากนี้ เรายังพบว่า ถ้า a | b และ b | a แล้ว a = b หรือ a = -b
นิยาม เรากำหนด greatest common divisor ของจำนวนเต็มสองจำนวน a, b ซึ่งไม่เป็นศูนย์ว่า
เป็นตัวหารร่วมของ a, b ที่มีค่ามากที่สุด เขียนแทนด้วย gcd(a, b) เช่น gcd(24, 30) = 6
- เราสามารถนิยาม d = gcd(a, b) ได้ว่า d | a และ d | b และถ้า c | a และ c | b แล้ว c | d
- ถ้า a และ b ไม่เป็นศูนย์ แล้ว gcd(a, b) เป็นจำนวนเต็มที่อยู่ระหว่าง 1 กับ min{|a|, |b|}
นอกจากนี้เราสามารถแสดงได้ว่า
- gcd(a, b) = gcd(b, a)
- gcd(a, b) = gcd(-a, b)
- gcd(a, b) = gcd(|a|, |b|)
- gcd(a, 0) = |a|
- gcd(a, ka) = |a| สำหรับทุกจำนวนเต็ม k
ทฤษฎี ถ้า a และ b เป็นจำนวนเต็มที่ไม่เป็นศูนย์ แล้ว gcd(a, b) เป็นจำนวนเต็มบวกที่เล็กที่สุดในเซต {a x + b y | x, y
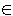 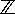 } }
Corollary สำหรับจำนวนเต็ม a และ b ใด ๆ ถ้า d | a และ d | b แล้ว d | gcd(a, b)
Corollary สำหรับจำนวนเต็ม a และ b และจำนวนเต็มที่ไม่เป็นลบ n ใด ๆ gcd(a n, b n) = n gcd(a, b)
Corollary สำหรับจำนวนเต็มบวก n, a และ b ถ้า n | a b และ gcd(a, n) = 1 แล้ว n | b
นิยาม เรากล่าวว่าจำนวนเต็ม a และ b เป็น relatively prime ถ้าตัวหารร่วมของ a และ b คือ 1
นั่นคือ gcd(a, b) = 1 เช่น 8 กับ 15 relatively prime
ทฤษฎี สำหรับจำนวนเต็ม a, b และ p ถ้า gcd(a, p) = 1 และ gcd(b, p) = 1 แล้ว gcd(a b, p) = 1
เรากล่าวว่าจำนวนเต็ม n1, n2, ..., nk เป็น pairwise relatively prime ถ้า
gcd(ni, nj) = 1 ทุก i 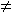 j j
ทฤษฎี สำหรับจำนวนเฉพาะ p และจำนวนเต็ม a, b ถ้า p | a b แล้ว p | a หรือ p | b
ทฤษฎี (Unique factorization) จำนวนประกอบ a สามารถเขียนในรูปผลคูณของจำนวนเฉพาะได้เพียงหนึ่งแบบเท่านั้นคือ
- a = p1e1p2e2...prer
เมื่อ pi เป็นจำนวนเฉพาะที่ p1 < p2 < ... < pr และ ei เป็นจำนวนเต็มบวก
เช่น 6000 = 24 × 3 × 53
การหาตัวหารร่วมมาก Greatest common divisor
ในส่วนนี้เราจะสนใจ เฉพาะจำนวนเต็มบวกเท่านั้น โดยทฤษฎี เราสามารถคำนวณ gcd(a, b) สำหรับจำนวนเต็มบวก a, b
ได้จาก factor ของ a และ b คือ
- a = p1e1p2e2...prer
- b = p1f1p2f2...prfr
- ได้คือ gcd(a,b) = p1min{e1, f1}p2min{e2, f2}...prmin{er, fr}
แต่วิธีการคำนวณดังกล่าวจะใช้เวลาในการคำนวณที่มากเกินไป เราจะใช้ Euclid's algorithm ในการหา gcd(a, b)
ทฤษฎี (GCD recursion theorem) สำหรับจำนวนเต็มที่ไม่เป็นลบ b และจำนวนเต็มบวก a,
- gcd(a, b) = gcd(b, a mod b)
Euclid's algorithm
Euclid(a, b)
ข้อมูลเข้า a แทนจำนวนเต็มบวก และ b แทนจำนวนเต็มที่ไม่เป็นลบ
ข้อมูลออก ตัวหารร่วมมากของ a, b
1. if b = 0
2. then return a
3. else
4. return Euclid(b, a mod b)
5. endif
ตัวอย่างของการทำงานของ Euclid เช่น การหา gcd(30, 21)
EUCLID(30, 21) = EUCLID(21, 9) = EUCLID(9, 3) = EUCLID(3, 0) = 3
ความถูกต้องของ Euclid's algorithm ได้จากทฤษฎี GCD recursion theorem และ ถ้า b = 0, gcd(a, b) = gcd(a, 0) = a
โดยที่ EUCLID algorithm หยุดทำงานเสมอ เนื่องจากค่า b ที่ลดลงทุกการเรียกใช้ recursive การวิเคราะห์เวลาในการทำงานของขั้นตอนวิธี Euclid
เราจะเปรียบเทียบกับลำดับ Fibonacci โดยที่ F1 = 0, F2 = 1, Fk+2 = Fk+1 + Fk
Lemma ถ้า a > b  0 และ EUCLID(a, b) มีการเรียก
อย่างน้อย k ครั้งแล้ว a 0 และ EUCLID(a, b) มีการเรียก
อย่างน้อย k ครั้งแล้ว a  Fk+1 และ b Fk+1 และ b  Fk
Fk
ทฤษฎี (Lame's theorem)
สำหรับจำนวนเต็ม k  1 ถ้า a > b 1 ถ้า a > b  0
และ b < Fk แล้ว EUCLID(a, b) จะถูกเรียกไม่เกิน k ครั้ง 0
และ b < Fk แล้ว EUCLID(a, b) จะถูกเรียกไม่เกิน k ครั้ง
เราสามารถแสดงขอบเขตบนของ Lame's theorem ได้ โดยพิจารณาลำดับ Fibonacci
EUCLID(F3, F2) จะได้จากการเรียกเพียงหนึ่งครั้ง และสำหรับ k  2
เราได้ว่า Fk+1 mod Fk = Fk-1 ดังนั้น 2
เราได้ว่า Fk+1 mod Fk = Fk-1 ดังนั้น
- gcd(Fk+1, Fk) = gcd(Fk, (Fk+1 mod Fk)) = gcd(Fk,
Fk-1)
ดังนั้น EUCLID(Fk+1, Fk) จะถูกเรียกเพียง k-1 ครั้ง
เพราะว่า Fk ประมาณได้ เป็น O(2k) ดังนั้นจำนวนครั้งในการเรียกคือ O(lg b)
Extended form of Euclid's algorithm
เราต้องการเขียนขั้นตอนวิธีในการคำนวณค่าของ gcd และค่าของ x, y ที่ทำให้
- d = gcd(a, b) = a x + b y
EXTEND-EUCLID(a, b)
ข้อมูลเข้า a แทนจำนวนเต็มที่ไม่เป็นลบ และ b แทนจำนวนเต็มบวก
ข้อมูลออก d ตัวหารร่วมมากของ a, b และค่า x, y ที่ทำให้ d = a x + b y
1. if b = 0
2. then return (a, 1, 0)
3. endif
4. (d', x', y') = EXTEND-EUCLID(b, a mod b)
5. (d, x, y) = (d', y', x' - 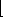 a/ b a/ b 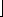 y')
6. return (d, x, y) y')
6. return (d, x, y)
ขั้นตอนวิธีนี้ใช้จำนวนรอบเท่ากับขั้นตอนวิธีของ EUCLID แต่ต่างกันที่เราได้ค่า x และ y ในตอนท้าย เราสามารถแสดงได้ว่าค่า x, y ที่ได้ใช่คำตอบจริง
โดยใช้อุปนัยในการพิสูจน์
กำหนดให้ P(n) แทนข้อความ EXTEND-EUCLID(a, b) ที่ถูกเรียกใช้ n ครั้งแล้วหยุด (ไม่มีการเรียกใช้ Recursive ต่อ) จะให้คำตอบ d = a x + b y = gcd(a, b)
- พื้นฐานของการอุปนัย ในกรณีที่ EXTEND-EUCLID(a, b) ที่ถูกเรียกใช้ 1 ครั้งแล้วหยุด เราได้ว่า b = 0, ดังนั้น gcd(a, b) = gcd(a, 0) = a =
a × 1 + b × 0 ดังนั้นคำตอบที่ส่งกลับคือ (a, 1, 0) เป็นคำตอบที่ถูกต้อง สรุปได้ว่า P(1) เป็นจริง
- ขั้นอุปนัย สมมติว่า P(k) เป็นจริง
พิจารณาในกรณี P(k+1) นั้นคือ EXTEND-EUCLID(a, b) ถูกเรียกใช้ k+1 ครั้ง เราจะผ่านมาบรรทัดที่ 4 ซึ่งมีการเรียกใช้
EXTEND-EUCLID เพียง k ครั้งแล้วหยุด โดยสมมติฐานของอุปนัยได้ว่า
- d' = gcd(b, a mod b) = b x' + (a mod b) y'
ในกรณีนี้เราพบว่า gcd(a, b) = gcd(b, a mod b) = d' นั้นคือ d = d' เป็นคำตอบที่ถูกต้อง และ
- d = d' = b x' + (a mod b) y' = b x' + (a -
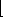 a/ b a/ b
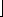 b) y' b) y'
= a y' + b (x' - 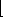 a/ b a/ b
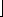 y' y'
การเลือก x = y' และ y = x' - 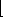 a/ b a/ b 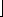 y'
จึงได้คำตอบตามที่ต้องการ y'
จึงได้คำตอบตามที่ต้องการ
สรุปว่าขั้นตอน EXTEND-EUCLID ได้คำตอบจริง
|