เลขคณิตมอดุลาร์
เราสามารถเปรียบเทียบการคำนวณเลขคณิตมอดุลาร์ เหมือนกับการคำนวณเลขคณิตปกติ x เพียงแต่ว่าค่าที่คำนวณได้จะตกอยู่
ในช่วง {0, 1, 2, ..., n-1} โดยที่ค่าของตัวเลขนั้นคือ x mod n โดยที่การคำนวณดังกล่าว สามารถอธิบายได้โดยใช้ ทฤษฎีกลุ่ม
Finite group
ให้ group (S,  ) ประกอบด้วยเซต S กับตัวกระทำการ ) ประกอบด้วยเซต S กับตัวกระทำการ
 ซึ่งนิยามบน S ดังนี้ ซึ่งนิยามบน S ดังนี้
- Closure: ทุก a, b
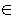 S, a S, a  b b
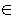 S S
- Identity: มีสมาชิกตัวหนึ่งเรียก e
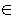 S ซึ่ง e S ซึ่ง e
 a = a a = a  e = a สำหรับทุกค่า a e = a สำหรับทุกค่า a
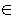 S S
- Associativity: ทุก a, b, c
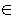 S, เราได้ว่า (a S, เราได้ว่า (a
 b) b)  c = a c = a
 (b (b  c) c)
- Inverses: ทุก a
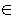 S, เราจะมีสมาชิก b เพียงหนึ่งตัวใน S ซึ่ง
a S, เราจะมีสมาชิก b เพียงหนึ่งตัวใน S ซึ่ง
a  b = b b = b  a = e a = e
ตัวอย่างของ group คือ ( , +) ของจำนวนเต็มภายใต้การบวก โดยที่ 0 คือเอกลักษณ์การบวก
และตัวผกผัน (inverse) ของ a คือ -a , +) ของจำนวนเต็มภายใต้การบวก โดยที่ 0 คือเอกลักษณ์การบวก
และตัวผกผัน (inverse) ของ a คือ -a
ในกรณีที่ group (S,  ) สอดคล้องกับ commutative law นั่นคือ ทุก a, b ใน S ) สอดคล้องกับ commutative law นั่นคือ ทุก a, b ใน S
- a
 b = b b = b  a a
เราจะเรียก group นี้ว่า abelian group
ถ้า group (S,  ) โดยที่ |S| < ) โดยที่ |S| < 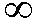 แล้ว เราเรียก (S,
แล้ว เราเรียก (S,  ) ว่า finite group ) ว่า finite group
นิยาม group โดยใช้การบวกมอดุลาร์ และการคูณมอดุลาร์
เราสามารถสร้างกลุ่มของ finite abelian groups ภายใต้การบวกและการคูณมอดุลาร์ n เมื่อ n เป็นจำนวนเต็มบวก ซึ่ง group
เหล่านี้จะมีการนิยามสมาชิกโดยใช้ equivalence class ของจำนวนเต็มมอดุลาร์ n กำหนดให้ a  a' (mod n) และ b
a' (mod n) และ b  b' (mod n) จะได้ว่า b' (mod n) จะได้ว่า
- a + b
 a' + b' (mod n) และ a' + b' (mod n) และ
- ab
 a'b' (mod n) a'b' (mod n)
โดยเราจะนิยามตัวแทนของสมาชิกคือ ค่าจำนวนเต็มที่ไม่เป็นลบที่เล็กที่สุด จากนิยามดังกล่าว เราสามารถนิยาม
( n, +n) โดยที่การคำนวณทั้งหมดจะให้ค่าตัวแทนใน n, +n) โดยที่การคำนวณทั้งหมดจะให้ค่าตัวแทนใน
 n ออกมา เราจะเรียกกลุ่มนี้ว่า additive group modulo n จากนิยามเราจะได้ว่า ขนาดของ
( n ออกมา เราจะเรียกกลุ่มนี้ว่า additive group modulo n จากนิยามเราจะได้ว่า ขนาดของ
( n, +n) เท่ากับ n n, +n) เท่ากับ n
ทฤษฎี ( n, +n) เป็น finite abelian group n, +n) เป็น finite abelian group
และเราจะนิยาม multiplicative group modulo n คือ ( *n, *n)
โดยที่สมาชิกใน group คือ สมาชิกของ *n, *n)
โดยที่สมาชิกใน group คือ สมาชิกของ  n ที่เป็นจำนวนเฉพาะสัมพัทธ์กับ n n ที่เป็นจำนวนเฉพาะสัมพัทธ์กับ n
- (
 *n, *n) = {[a]n *n, *n) = {[a]n
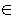  n : gcd(a, n) = 1 } n : gcd(a, n) = 1 }
ตัวอย่างเช่น  *15 = {1, 2, 4, 7, 8, 11, 13, 14} *15 = {1, 2, 4, 7, 8, 11, 13, 14}
ทฤษฎี ( *n, *n) เป็น finite abelian group *n, *n) เป็น finite abelian group
สังเกตว่า
- a x
 b (mod n) หมายถึง [a]n *n [x]n =
[b]n b (mod n) หมายถึง [a]n *n [x]n =
[b]n
เพื่อความสะดวกเราจะเขียน + และ * เหมือนปกติ แต่ให้นึกไว้ว่าเป็นการบวกและการคูณของจำนวนเต็มมอดุลาร์ n เรานิยาม (multiplicative) inverse ของ
a คือ a-1 mod n และการหาร a/b  a b-1 (mod n) เช่นใน a b-1 (mod n) เช่นใน
 *15, 7-1 *15, 7-1  13
(mod 15) เพราะ 7 * 13 13
(mod 15) เพราะ 7 * 13  91 91  1
(mod 15) ดังนั้น 4/7 1
(mod 15) ดังนั้น 4/7  4*13 4*13  7
(mod 15) 7
(mod 15)
เรากำหนดขนาดของ  *n ให้คือ ø(n) ฟังก์ชันดังกล่าวถูกเรียกว่า
Euler's phi function ซึ่งจะมีค่าสอดคล้องกับ *n ให้คือ ø(n) ฟังก์ชันดังกล่าวถูกเรียกว่า
Euler's phi function ซึ่งจะมีค่าสอดคล้องกับ
- ø(n) = n
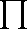 p | n(1 - 1/p) p | n(1 - 1/p)
เมื่อ p คือจำนวนเฉพาะที่หาร n ลงตัว (รวม n ด้วย ถ้า n เป็นจำนวนเฉพาะ)
เราได้ว่า ø(15) = 45(1 - 1/3)(1 - 1/5) = 24 ถ้าในกรณีที่ p เป็นจำนวนเฉพาะ เราได้ว่า
 *p = {1, 2, ..., p-1} และ ø(p) = p - 1 *p = {1, 2, ..., p-1} และ ø(p) = p - 1
ถ้า n เป็นจำนวนประกอบ เราได้ว่า ø(n) < n - 1
กำหนดให้ (S,  ) เป็น group และ S' ) เป็น group และ S' 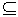 S
และ (S', S
และ (S',  ) เป็น group เราจะเรียก (S', ) เป็น group เราจะเรียก (S',  ) ว่า
subgroup ของ (S, ) ว่า
subgroup ของ (S,  ) )
ทฤษฎี (A closed subset of a finite group is a subgroup)
ถ้า (S,  ) เป็น finite group และ S' เป็นสับเซตของ S ที่มี e อยู่โดยที่ a ) เป็น finite group และ S' เป็นสับเซตของ S ที่มี e อยู่โดยที่ a
 b b 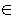 S' สำหรับทุกค่า a, b ซึ่งอยู่ใน S' และ
ถ้า a S' สำหรับทุกค่า a, b ซึ่งอยู่ใน S' และ
ถ้า a 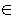 S' และ a S' และ a  b b
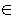 S' แล้ว b S' แล้ว b 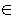 S'
เราได้ว่า S' เป็น subgroup S'
เราได้ว่า S' เป็น subgroup
เช่น {0, 2, 4, 6} เป็น subgroup ของ  8 8
ทฤษฎี (Lagrange's theorem)
ถ้า (S,  ) เป็น finite group และ (S', ) เป็น finite group และ (S',  ) เป็น
subgroup ของ S แล้ว | S' | จะเป็นค่าที่หาร | S | ลงตัว ) เป็น
subgroup ของ S แล้ว | S' | จะเป็นค่าที่หาร | S | ลงตัว
เรากล่าวว่า S' เป็น proper subgroup ของ S ถ้า S' 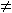 S S
บทแทรกถ้า S' เป็น proper subgroup ของ finite group S เราได้ว่า | S' | 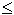 | S | / 2
| S | / 2
จากทฤษฎีที่กล่าวมา เราสามารถสร้าง subgroup จากสมาชิกตัวหนึ่งได้เสมอ เราจำนิยาม subgroup ที่ได้จาก a ว่า a(k) โดยที่
- a(k) =
 i = 1 a =
a i = 1 a =
a  a a  a a
 ... ...  a a
เช่นถ้าเราให้ a = 2 ใน group  6 เราได้ว่า a(1), a(2), ...
คือ 2, 4, 0, 2, 4, 0, ... 6 เราได้ว่า a(1), a(2), ...
คือ 2, 4, 0, 2, 4, 0, ...
ใน  n เราได้ว่า a(k) = ka mod n และใน n เราได้ว่า a(k) = ka mod n และใน
 *n เราได้ว่า a(k) = ak mod n เราเรียก subgroup generated
by a แทนด้วย <a> คือ *n เราได้ว่า a(k) = ak mod n เราเรียก subgroup generated
by a แทนด้วย <a> คือ
- <a> = {a(k): k
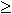 1} 1}
เรากล่าวว่า a generates subgroup <a> หรือ a คือ generator ของ <a> เพราะว่า S เป็น finite เราได้ว่า <a> เป็น finite
subset ของ S และเราพบว่า a(i)  a(j) = a(i+j) ดังนั้น
<a> มีสมบัติปิดภายใต้การบวก ตัวอย่างของ a(j) = a(i+j) ดังนั้น
<a> มีสมบัติปิดภายใต้การบวก ตัวอย่างของ  6 เราได้ว่า 6 เราได้ว่า
- <0> = {0}
- <1> = {0, 1, 2, 3, 4, 5}
- <2> = {0, 2, 4}
ในทำนองเดียวกัน  *7 เราได้ว่า *7 เราได้ว่า
- <1> = {1}
- <2> = {1, 2, 4}
- <3> = {1, 2, 3, 4, 5, 6}
เรากำหนดว่า order ของ a เขียนแทนด้วย ord(a) คือ จำนวนเต็มที่น้อยที่สุด t > 0 ซึ่ง a(t) = e
ทฤษฎี
สำหรับ finite group (S,  ) และ a ใน S, order ของสมาชิกจะเท่ากับ ขนาดของ subgroup
ที่ได้จาก a นั่นคือ ord(a) = |<a>| ) และ a ใน S, order ของสมาชิกจะเท่ากับ ขนาดของ subgroup
ที่ได้จาก a นั่นคือ ord(a) = |<a>|
บทแทรก ลำดับ a(1), a(2), ... เป็นคาบด้วยค่า t = ord(a) นั่นคือ
- a(i) = a(j) ก็ต่อเมื่อ i
 j (mod t) j (mod t)
เราสามารถนิยาม a(0) = e และ a(i) = a(i mod t) สำหรับทุกจำนวนเต็ม i
บทแทรก ให้ (S,  ) เป็น finite subgroup ด้วยเอกลักษณ์ e
จะได้ว่า ทุก a ใน S, a(|S|) = e ) เป็น finite subgroup ด้วยเอกลักษณ์ e
จะได้ว่า ทุก a ใน S, a(|S|) = e
การแก้สมการเชิงเส้นของเลขคณิตมอดุลาร์
เราสนใจผลเฉลยของสมการในรูป
- a x
 b (mod n) b (mod n)
เมื่อ n เป็นจำนวนเต็มที่มากกว่า 0 โดยเราทราบค่าของ a, b, n เราต้องการหาค่า x modulo n ที่ทำให้สมการข้างต้นจริง ซึ่งอาจไม่มีผลเฉลย
ผลเฉลยเพียงหนึ่ง หรือมากกว่า ก็ได้ ถ้าเรากำหนดให้ <a> แทน subgroup ของ
 n ที่ generated โดย a เราทราบว่า <a> = { a(x) : x > 0 }
= { a x mod n | x > 0 } นั่นคือผลเฉลย b เป็นคำตอบก็ต่อเมื่อ b n ที่ generated โดย a เราทราบว่า <a> = { a(x) : x > 0 }
= { a x mod n | x > 0 } นั่นคือผลเฉลย b เป็นคำตอบก็ต่อเมื่อ b 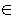 <a>
ทฤษฎีของ Lagrange บอกเราว่า | <a> | ต้องหาร n เราได้ว่า <a>
ทฤษฎีของ Lagrange บอกเราว่า | <a> | ต้องหาร n เราได้ว่า
ทฤษฎี สำหรับจำนวนเต็มบวก a และ n ใด ๆ ถ้า d = gcd(a, n) แล้ว
- <a> = <d> = {0, d, 2d, 3d, ..., ((n/d) - 1)d}
ดังนั้น |<a>| = n/d
บทแทรก a x  b (mod n) มีคำตอบ ก็ต่อเมื่อ gcd(a, n) | b b (mod n) มีคำตอบ ก็ต่อเมื่อ gcd(a, n) | b
บทแทรก a x  b (mod n) อาจมีคำตอบ d ค่าที่แตกต่างกัน
ใน modulo n เมื่อ d = gcd(a, n) หรือ อาจไม่มีคำตอบเลย b (mod n) อาจมีคำตอบ d ค่าที่แตกต่างกัน
ใน modulo n เมื่อ d = gcd(a, n) หรือ อาจไม่มีคำตอบเลย
ทฤษฎีบท ให้ d = gcd(a, n) และสมมติว่า d = a x' + n y' สำหรับบางค่าของ x', y' ถ้า d | b แล้ว สมการ
a x  b (mod n) มีหนึ่งผลเฉลยที่มีค่า x0 เมื่อ x0 = x'(b/d) mod n b (mod n) มีหนึ่งผลเฉลยที่มีค่า x0 เมื่อ x0 = x'(b/d) mod n
ทฤษฎีบท ให้ d = gcd(a, n) และสมมติว่า a x  b (mod n)
มีผลเฉลย หนึ่งคำตอบที่มีค่า x0 เมื่อ x0 = x'(b/d) mod n b (mod n)
มีผลเฉลย หนึ่งคำตอบที่มีค่า x0 เมื่อ x0 = x'(b/d) mod n
ทฤษฎีบท สมมติว่า a x  b (mod n) มีผลเฉลย โดย
d = gcd(a, n) (นั่นคือเราได้ว่า d | b ) และ x0 เป็นผลเฉลยตัวหนึ่ง แล้ว เราได้ว่าสมการนี้จะมีผลเฉลย d ตัวที่ต่างกัน modulo n โดยที่
xi = x0 + i (n/d) ทุก i = 1, 2, ..., d - 1 b (mod n) มีผลเฉลย โดย
d = gcd(a, n) (นั่นคือเราได้ว่า d | b ) และ x0 เป็นผลเฉลยตัวหนึ่ง แล้ว เราได้ว่าสมการนี้จะมีผลเฉลย d ตัวที่ต่างกัน modulo n โดยที่
xi = x0 + i (n/d) ทุก i = 1, 2, ..., d - 1
MODULAR-LINEAR-EQUATION-SOLVER(a, b, n)
ข้อมูลเข้า a, b แทนจำนวนเต็มที่ไม่เป็นลบ และ n แทนจำนวนเต็มบวก
ข้อมูลออก แสดงผลเฉลยทั้งหมดของ a x  b (mod n)
ถ้ามี b (mod n)
ถ้ามี
1. (d, x', y') = EXTENDED-EUCLID(a, n)
2. if d | b
3. then x0 = x'(b/d) mod n
4. for i = 0 to d-1
5. print (x0 + i(n/d)) mod n
6. endfor
7. else
8. print "no solution"
9. endif
บทแทรก สำหรับทุก n > 1 ถ้า gcd(a, n) = 1 และ a x  b (mod n)
มีผลเฉลย แล้วจะได้ว่า a x b (mod n)
มีผลเฉลย แล้วจะได้ว่า a x  b (mod n) มีผลเฉลยเพียงหนึ่งตัวเท่านั้น modulo n b (mod n) มีผลเฉลยเพียงหนึ่งตัวเท่านั้น modulo n
ในกรณีที่ b = 1 นั่นคือ x จะเป็น multiplicative inverse ของ a modulo n
บทแทรก สำหรับทุก n > 1 ถ้า gcd(a, n) = 1 แล้ว a x  1 (mod n)
จะมีผลเฉลยเพียงหนึ่ง modulo n หรือไม่มีผลเฉลย 1 (mod n)
จะมีผลเฉลยเพียงหนึ่ง modulo n หรือไม่มีผลเฉลย
|