1. for i = 1 to k;
2. C[i] = 0;
3. endfor
4. for j = 1 to length[A];
5. C[A[j]] = C[A[j]] + 1;
6. endfor
7. for i = 2 to k;
8. C[i] = C[i] + C[i-1];
9. endfor
10. for j = length[A] downto 1;
11. (B[C[A[j]]], C[A[j]]) = (A[j], C[A[j]]-1);
12. endfor
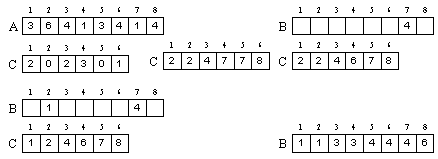
ตัวอย่างที่ 1 จงเรียงข้อมูลต่อไปนี้โดยใช้ Counting sort
3, 6, 4, 1, 3, 4, 1, 4
8, 2, 3, 1, 3, 2, 5, 6, 7
การจัดเรียงโดยใช้ฐาน Radix sort
การจัดเรียงประเภทนี้ใช้กับข้อมูลที่สามารถจัดได้เป็นกลุ่ม ๆ เช่น การจัดเรียงตัวเลขฐานสิบ
โดยเราแบ่งกลุ่มตามค่าของตัวเลขโดดในแต่ละตำแหน่ง หลังจากที่แต่ละกลุ่มถูกแบ่งแล้วเราจึงจัดเรียง อาจเริ่มจากหลักที่มากที่สุด แล้วลดหลั่นลงมาจนถึง
หลักหน่วย หรือ จัดเรียงโดยเริ่มจากหลักหน่วยไปหลักสิบไปหลักร้อย และต่อไปเรื่อย ๆ จนครบทุกหลัก สำหรับขั้นตอนวิธีที่เราเขียนจะใช้
หลักการแบบที่สอง คือเรียงตัวเลขโดยเริ่มจากกลุ่มเลขโดดในหลักหน่วย แล้วไล่ขึ้นไปจนถึงหลักสุดท้าย แต่เราต้องใช้วิธีการเรียงลำดับที่มีสมบัติ stable
ขั้นตอนวิธีการจัดลำดับที่มีสมบัติ stable หมายความว่า ถ้าข้อมูลสองจำนวนใด ๆ มีค่าเปรียบเทียบที่เหมือนกันแล้ว ลำดับของการจัดเรียงของ
ข้อมูลทั้งสองตัวนั้นจะอยู่ในลำดับเดียวกับข้อมูลก่อนถูกจัดเรียง เช่น
11, 32, 43, 34, 15 หลังจากผ่านขั้นตอนการจัดลำดับที่ stable จะได้
11, 15, 32, 34, 43 เมื่อเลขดรรชนีล่างบ่งบอกลำดับเริ่มต้นก่อนการจัดเรียง
ขั้นตอนวิธี RADIX-SORT(A, d) เมื่อ A เป็นข้อมูลเข้า n ที่แต่ละค่ามีจำนวนตัวเลขสูงสุด d ตัว และ d เป็นตำแหน่งสุดท้าย
(most-significant digit) ของตัวเลขใน A
ข้อมูลเข้า A[1..n], d
ข้อมูลออก A[1..n] โดยที่ A[1] < A[2] < A[3] < . . . < A[n]
RADIX-SORT(A, d)
1. for i = 1 to d
2. use a stable sort to sort array A on digit i
3. endfor
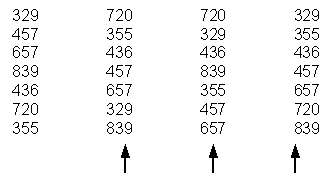
ตัวอย่างที่ 2 จงเรียงข้อมูลต่อไปนี้โดยใช้ Radix sort กับ Insertion sort แทน stable sort
- 329, 457, 657, 839, 436, 720, 355
- 80, 22, 13, 01, 56, 22, 51, 62, 43
- 87988, 82834, 23432, 26679, 58740, 15423, 33456
การจัดเรียงโดยใส่กล่อง Bucket sort
ถ้าเราพบว่าข้อมูลมีการกระจายแบบ uniform บนช่วง [0, 1) โดยเราจะแบ่งช่วง [0, 1) ออกเป็น n ช่วงย่อยเท่า ๆ กันใส่ในกล่อง
(buckets) แล้วเรียงข้อมูลในแต่ละกล่อง ข้อมูลทั้งหมดที่เรียงได้จากการนำข้อมูลที่ถูกจัดเรียงออกมาโดยการไล่ดึงออกจากแต่ละกล่อง
ขั้นตอนวิธี BUCKET-SORT(A) เมื่อ A เป็นข้อมูลเข้า n ที่แต่ละค่าเป็นจำนวนระหว่างช่วง [0, 1)
ข้อมูลเข้า A[1..n]
ข้อมูลออก A[1..n] โดยที่ A[1] < A[2] < A[3] < . . . < A[n]
BUCKET-SORT(A)
1. n = length[A]
2. for i = 1 to n
3. insert A[i] into list B[ 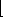 n A[i] n A[i] 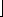 ]
4. endfor
5. for i = 0 to n-1
6. sort list B[i] with insertion sort
7. endfor
8. concatenate the list B[0], B[1], ..., B[n-1] in order ]
4. endfor
5. for i = 0 to n-1
6. sort list B[i] with insertion sort
7. endfor
8. concatenate the list B[0], B[1], ..., B[n-1] in order
จงเรียงข้อมูลต่อไปนี้โดยใช้ Bucket sort
- 0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.68
- 0.80, 0.22, 0.13, 0.01, 0.56, 0.32, 0.71, 0.62, 0.94
- 0.3487, 0.828, 0.44435, 0.234, 0.667, 0.970, 0.5874 0.032, 0.154, 0.489, 0.3345, 0.6987
|
|
Home |
Previous |
Next
|
|
© Copyright by กรุง สินอภิรมย์สราญ
|