ปัญหาการจับคู่สายอักขระ string matching problem
กำหนดให้ข้อความ (Text) T[1..n] เก็บเนื้อหาที่ต้องการค้น และแบบรูป (Pattern) ที่ต้องการคือ P[1..m] โดยที่ตัวอักขระใน T
และ P มาจากเซตของสัญลักษณ์ใน 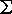
เรากล่าวว่า P ปรากฎด้วยการเลื่อน s (ปรากฎที่ตำแหน่ง s) ในข้อความ T ถ้า 0  s s
 n - m และ T[s+1, ..., s+m] = P[1,...,m] หรือเขียนได้เป็น T[s+j] = P[j] สำหรับ 1 n - m และ T[s+1, ..., s+m] = P[1,...,m] หรือเขียนได้เป็น T[s+j] = P[j] สำหรับ 1
 j j  m เราจะเรียกว่าแบบรูป P ที่ปรากฎที่ตำแหน่ง
s ของข้อความ T นี้ว่าเป็นการเลื่อนที่สมเหตุสมผล (valid shift) มิฉะนั้นเราจะเรียกว่าเป็นการเลื่อนที่ไม่สมเหตุสมผล (invalid shift) m เราจะเรียกว่าแบบรูป P ที่ปรากฎที่ตำแหน่ง
s ของข้อความ T นี้ว่าเป็นการเลื่อนที่สมเหตุสมผล (valid shift) มิฉะนั้นเราจะเรียกว่าเป็นการเลื่อนที่ไม่สมเหตุสมผล (invalid shift)
นิยามที่ควรรู้จัก
เราเขียน 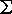 * แทนเซตของสายอักขระจำกัดทั้งหมดที่มาจาก * แทนเซตของสายอักขระจำกัดทั้งหมดที่มาจาก
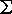 และเราใช้ และเราใช้ 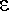 แทนสัญลักษณ์ว่าง
ขนาดของสายอักขระ x แทนด้วย |x| และ xy แทนการเชื่อมของสายอักขระ x และ y ตามลำดับ แทนสัญลักษณ์ว่าง
ขนาดของสายอักขระ x แทนด้วย |x| และ xy แทนการเชื่อมของสายอักขระ x และ y ตามลำดับ
เรากล่าวว่า w เป็นสายอักขระเติมหน้า (prefix) ของ x ถ้ามีสายอักขระ y ใน 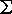 *
ซึ่ง x = wy และเรากล่าวว่า z เป็นสายอักขระเติมท้าย (suffix) ของ x ถ้ามีสายอักขระ y ใน *
ซึ่ง x = wy และเรากล่าวว่า z เป็นสายอักขระเติมท้าย (suffix) ของ x ถ้ามีสายอักขระ y ใน
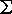 * ซึ่ง x = yz * ซึ่ง x = yz
ดังนั้น 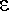 เป็นทั้งสายอักขระเติมหน้าและสายอักขระเติมท้ายของทุกสายอักขระ เป็นทั้งสายอักขระเติมหน้าและสายอักขระเติมท้ายของทุกสายอักขระ
Overlapping-suffix lemma
กำหนดให้ x, y, z เป็นสายอักขระซึ่ง x และ y เป็นสายอักขระเติมท้ายของ z ถ้า | x |  | y | แล้วจะได้ว่า x เป็นสายอักขระเติมท้ายของ y และถ้า | x |
| y | แล้วจะได้ว่า x เป็นสายอักขระเติมท้ายของ y และถ้า | x |  | y | จะได้ว่าสายอักขระ y
เป็นสายอักขระเติมท้ายของ x และในกรณีที่ | x | == | y | จะได้ว่าสายอักขระ x เหมือนกับสายอักขระ y | y | จะได้ว่าสายอักขระ y
เป็นสายอักขระเติมท้ายของ x และในกรณีที่ | x | == | y | จะได้ว่าสายอักขระ x เหมือนกับสายอักขระ y
เราสามารถเขียนขั้นตอนวิธีในการหาแบบรูปที่ต้องการแบบตรงไปตรงมาดังนี้ (naive string-matching algorithm)
NAIVE-STRING-MATCHER(T, P)
ข้อมูลเข้า T คือข้อความที่จะถูกค้น และ P คือแบบรูปที่จะหาใน T
ข้อมูลออก s คือตำแหน่งที่พบแบบรูป P ในข้อความ T และให้ค่า -1 ถ้าไม่พบ
1. (n, m) = (length(T), length(P))
2. for s = 0 to n - m
3. if P[1..m] == T[s+1, ..., s+m] then
4. return s
5. endif
6. endfor
7. return -1
เราจะพบว่าขั้นตอนวิธีนี้ไม่มีประสิทธิภาพ เนื่องจากเรามีการเปรียบเทียบซ้ำๆ กันของสายอักขระเติมหน้าของแบบรูป P โดยไม่จำเป็น
ขั้นตอนวิธีของ Rabin-Karp
พิจารณา 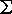 = {0, 1, 2, ..., 9} สายอักขระที่เราพิจารณาคือ
ชุดของตัวเลขฐานสิบ หมายความว่า สายอักขระขนาด k ที่เราสนใจคือจำนวนที่มีตัวเลขปรากฎอยู่ k ตัว สำหรับแบบรูป P[1..m] เรากำหนดให้ p
คือค่าที่ได้จากแบบรูป P[1..m] และในทำนองเดียวกันเรากำหนดให้ ts แทนค่าของตัวเลข m ตัวจากข้อความ T[s+1, ..., s+m] โดยที่ s =
0, 1, ..., n-m เราพบว่า = {0, 1, 2, ..., 9} สายอักขระที่เราพิจารณาคือ
ชุดของตัวเลขฐานสิบ หมายความว่า สายอักขระขนาด k ที่เราสนใจคือจำนวนที่มีตัวเลขปรากฎอยู่ k ตัว สำหรับแบบรูป P[1..m] เรากำหนดให้ p
คือค่าที่ได้จากแบบรูป P[1..m] และในทำนองเดียวกันเรากำหนดให้ ts แทนค่าของตัวเลข m ตัวจากข้อความ T[s+1, ..., s+m] โดยที่ s =
0, 1, ..., n-m เราพบว่า
- ts == p ก็ต่อเมื่อ T[s+1..s+m] = P[1...m]
เราสามารถคำนวณจำนวนเต็ม p ที่ใช้ Running time เท่ากับ O(m) และคำนวณค่าของ ti โดยใช้ Running time O(n)
จากขั้นตอนวิธีการคำนวณของ Horner's rule
- p = P[m] + 10(P[m-1] + 10(P[m-2] + ... + 10(P[2] + 10 P[1])...)
เราคำนวณค่าของ t0 โดยใช้หลักการเดียวกัน แต่สำหรับ t1, ..., tn
เราใช้วิธีการที่ง่ายขึ้นจาก recurrence relation ดังนี้
- ts+1 = 10(ts - 10m-1 T[s+1]) + T[s+m+1]
ปัญหาที่พบคือค่าของ p และ ts จะเป็นค่าที่ใหญ่มาก ซึ่งคอมพิวเตอร์โดยทั่วไปอาจไม่สามารถเก็บได้ เราจึงต้องการลดขนาดของตัวเลขนี้
โดยเก็บค่าของตัวเลข modulo q เมื่อ q เป็นจำนวนเฉพาะที่มีขนาดเหมาะสมกับเครื่องที่ใช้อยู่
สำหรับ 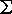 = {0, 1, .., d-1} เราจะเลือกจำนวนเต็ม q โดยที่ d q สามารถเก็บได้ในหนึ่ง
computer word ดังนั้นเราได้ recurrence relation ใหม่คือ = {0, 1, .., d-1} เราจะเลือกจำนวนเต็ม q โดยที่ d q สามารถเก็บได้ในหนึ่ง
computer word ดังนั้นเราได้ recurrence relation ใหม่คือ
- ts+1 = (d (ts - h T[s+1]) + T[s+m+1]) mod q
เมื่อ h = dm-1 mod q
จากการคำนวณนี้เราได้ว่า ts = p (mod q) ไม่สามารถสรุป ts = p ได้ แต่ถ้า ts
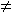 p (mod q) เราได้ว่า ts p (mod q) เราได้ว่า ts 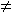 p เสมอ p เสมอ
ดังนั้นเราสามารถตรวจว่าแบบรูปใดไม่อยู่ในข้อความได้โดยง่าย และถ้าพบว่า ts = p (mod q) เราเพียงเพิ่มการทดสอบ
T[s+1, ..., s+m] = P[1..m] เพิ่มเติม
RABIN-KARP-MATCHER(T, P, d, q)
ข้อมูลเข้า T คือข้อความที่จะถูกค้น, P คือแบบรูปที่จะหาในข้อความ T, d คือฐานของตัวเลข และ q คือจำนวนเฉพาะ
ข้อมูลออก s คือตำแหน่งที่พบแบบรูป P ในข้อความ T และให้ค่า -1 ถ้าไม่พบ
1. (n, m) = (length(T), length(P))
2. h = d^(m-1) mod q
3. (p, t0) = (0, 0)
4. for i = 1 to m
5. (p, t0) = (d*p + P[i]) mod q, d*t0 + T[i]) mod q)
6. endfor
7. for s = 0 to n - m
8. If p == ts
9. if P[1..m] == T[s+1...s+m]
10. return s
11. endif
12. endif
13. if s < n - m
14. ts+1 = (d*(ts - T[s+1]*h + T[s+m+1]) mod q
15. endif
16. endfor
17. return -1
|