นิพจน์ปกติ (Regular expression)
จากบทที่แล้วเราสามารถใช้ออโตมาตาจำกัดในการแก้ปัญหาการจดจำรูปแบบของสายอักขระในเซตได้ แต่เราอาจสงสัยว่า ออโตมาตาจำกัดแต่ละแบบ
มีความสามารถต่างกันหรือไม่ อย่างไร ก่อนเราจะกล่าวถึงความสามารถของออโตมาตาจำกัดแบบต่างๆ เราจะนิยามภาษาประเภทหนึ่งที่เรียกว่า ภาษาปกติ ดังนี้
นิยาม กำหนดให้  เป็นชุดตัวอักษร
นิพจน์ปกติ (regular expression) เป็นสัญลักษณ์ที่ใช้แทนสับเซตของ เป็นชุดตัวอักษร
นิพจน์ปกติ (regular expression) เป็นสัญลักษณ์ที่ใช้แทนสับเซตของ  *
ซึ่งนิยามโดยวิธีเรียกซ้ำ (recursive) ดังนี้ *
ซึ่งนิยามโดยวิธีเรียกซ้ำ (recursive) ดังนี้
-
 เป็นนิพจน์ปกติ แทนเซตว่าง ( เป็นนิพจน์ปกติ แทนเซตว่าง ( ) )
-
 เป็นนิพจน์ปกติ แทน
{ เป็นนิพจน์ปกติ แทน
{ } }
- สำหรับแต่ละ a
  ,
a เป็นนิพจน์ปกติ แทน {a} ,
a เป็นนิพจน์ปกติ แทน {a}
- ถ้า r และ s เป็นนิพจน์ปกติ แทนเซต R และ S ตามลำดับแล้ว (r+s), (rs), (r*)
เป็นนิพจน์ปกติแทน R
 S, RS, R* ตามลำดับ S, RS, R* ตามลำดับ
และนิพจน์ปกติเขียนได้จากกฎ 4 ข้อนี้เท่านั้น
ข้อตกลง
- ri หมายถึง rr...r ต่อกัน i ครั้ง
- เราสามารถลดรูปการเขียนเช่น ((0(1*))+0) เขียนแทนด้วย 01*+0
โดยที่ความสำคัญของลำดับการใช้ตัวกระทำการ (operator) เป็นดังนี้ * มีความสำคัญสูงสุด ตามด้วยการต่อกันของภาษา และ + มีความสำคัญต่ำสุด
- L(r) คือเซตที่มี r เป็นนิพจน์ปกติที่แทนเซตนั้น
- a+ หมายถึง aa* เมื่อ a


- ถ้า r, s เป็นนิพจน์ปกติ แล้ว r = s หมายถึง L(r) = L(s)
ตัวอย่างของนิพจน์ปกติ เช่น 0, 1*, 01*, 00+1,
 , 1 + , 1 + 
นิยาม ภาษาปกติ
L เป็น ภาษาปกติ (regular language) หรือ เซตปกติ (regular set) ก็ต่อเมื่อ มีนิพจน์ปกติ r ที่ L = L(r)
ตัวอย่าง 1 กำหนด  = {0, 1} = {0, 1}
- 00 เป็นนิพจน์ปกติแทน {00} เพราะ L(00) = {00}
- (0+1)* เป็นนิพจน์ปกติแทน {0, 1}* ดังนั้น L((0+1)*)
= {
 , 0, 1, 00, 01, 10, 11, 000, ... } = , 0, 1, 00, 01, 10, 11, 000, ... } =  * *
- (0+1)*00(0+1)* เป็นนิพจน์ปกติแทน {x
 {0, 1}* | x ต้องมี 00 ปรากฎอย่างน้อย 1 ครั้ง } = {00, 000, 100, 000, 001, ...}
{0, 1}* | x ต้องมี 00 ปรากฎอย่างน้อย 1 ครั้ง } = {00, 000, 100, 000, 001, ...}
- (0+10)* เป็นนิพจน์ปกติแทน {0, 10}* = {
 ,
0, 10, 00, 010, 100, 000, ...} ,
0, 10, 00, 010, 100, 000, ...}
- (1+10)2 = (1+10)(1+10) เป็นนิพจน์ปกติแทน {x
 {0, 1}* | x = w1w2 เมื่อ w1, w2
{0, 1}* | x = w1w2 เมื่อ w1, w2  {1, 10} } = {11, 110, 101, 1010} ดังนั้น (1+10)(1+10) = 11+110+101+1010
{1, 10} } = {11, 110, 101, 1010} ดังนั้น (1+10)(1+10) = 11+110+101+1010
ทฤษฎีบท ถ้า r เป็นนิพจน์ปกติแล้วเราสามารถสร้างออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้ายโดย- ที่ยอมรับ L(r) ได้
ที่ยอมรับ L(r) ได้
พิสูจน์ ให้ r เป็นนิพจน์ปกติ
วิธีการพิสูจน์คือ เราจะสร้าง M ตามนิยามเวียนเกิดของนิพจน์ปกติ พร้อมรับประกันว่า L(M) = L(r) โดยใช้อุปนัยเข้มทางคณิตศาสตร์
การสร้าง M เราจะบังคับให้มีสถานะยอมรับเพียงสถานะเดียวเพื่อความง่ายต่อการพิสูจน์ (การทำเช่นนี้เป็นไปได้เสมอ เพราะถ้าเรามีสถานะยอมรับมากกว่าหนึ่งสถานะ เราเพียงสร้างสถานะใหม่แล้ว
เชื่อมฟังก์ชันการผ่านโดยใช้  จากสถานะยอมรับเดิมทั้งหมดไปสถานะนี้ แล้วกำหนดสถานะยอมรับใหม่ให้เป็นสถานะนี้เท่านั้น)
จากสถานะยอมรับเดิมทั้งหมดไปสถานะนี้ แล้วกำหนดสถานะยอมรับใหม่ให้เป็นสถานะนี้เท่านั้น)
เราใช้อุปนัยเข้มบน จำนวนการดำเนินการในนิพจน์ปกติ r
มูลฐานของการอุปนัย จำนวนการดำเนินการใน r เป็น 0
เราได้ว่า r =  , r = , r =  หรือ r = a เมื่อ a
หรือ r = a เมื่อ a  
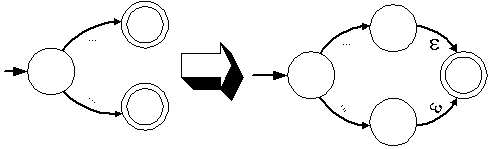
- รูปที่ 1, 2, 3 เป็นรูปของออโตมาตาจำกัดที่ยอมรับ L(M1) = L(
 ),
L(M2) = L( ),
L(M2) = L( ) และ L(M3) = L(a) ตามลำดับ ) และ L(M3) = L(a) ตามลำดับ
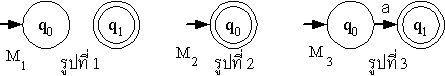
ขั้นตอนของการอุปนัย เราตั้งสมมติฐานของการอุปนัยว่า สำหรับนิพจน์ปกติใด ๆ ที่มีจำนวนดำเนินการ k โดยที่ k น้อยกว่า n และ
n > 0 เราสามารถสร้างออโตมาตาจำกัดเชิงไม่กำหนดที่ยอมรับภาษาของนิพจน์ปกตินั้นได้ โดยมีสถานะยอมรับเพียงสถานะเดียว
เราต้องการแสดงว่า สำหรับนิพจน์ปกติที่มีจำนวนดำเนินการเท่ากับ n เราจะสร้าง ออโตมาตาจำกัดเชิงไม่กำหนด แบ่งตามกรณีดังนี้
- กรณีที่ r = r1 + r2, จากสมมติฐานการอุปนัย เราจะมีเครื่องออโตมาตาจำกัดเชิงไม่กำหนด
สองเครื่อง M1, M2 ที่ยอมรับ L(r1), L(r2) ตามลำดับ
และมีสถานะยอมรับเพียงสถานะเดียว
เราสร้างออโตมาตาเครื่องใหม่ M โดยมีสถานะเริ่มต้นและสถานะยอมรับใหม่ ดังรูป
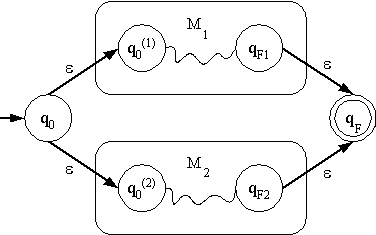
เราจะได้ว่า L(M) = L(M1)  L(M2) =
L(r1) L(M2) =
L(r1)  L(r2) = L(r1 +
r2) ตามที่ต้องการ L(r2) = L(r1 +
r2) ตามที่ต้องการ
ในเชิงคณิตศาสตร์ เราเขียนอธิบายเครื่องออโตมาตา M ได้ดังนี้
- M1 = (Q1,
 , ,
 1, q0(1), {qF1}) และ M2 =
(Q2, 1, q0(1), {qF1}) และ M2 =
(Q2,  , ,  2,
q0(2), {qF2}) โดยที่สถานะทั้งหมดในสองเครื่องต่างกันหมด 2,
q0(2), {qF2}) โดยที่สถานะทั้งหมดในสองเครื่องต่างกันหมด
- ให้ M = (Q1
 Q2 Q2
 {q0, qF}, {q0, qF},  , ,
 , q0, {qF}) เมื่อ q0 และ qF
เป็นสถานะใหม่ที่ไม่ปรากฎใน Q1 และ Q2 , q0, {qF}) เมื่อ q0 และ qF
เป็นสถานะใหม่ที่ไม่ปรากฎใน Q1 และ Q2
- และนิยาม
 ดังนี้ ดังนี้
 (q0, (q0,  )
= {q0(1), q0(2)} )
= {q0(1), q0(2)}
- สำหรับแต่ละ q
 Q1 Q1  Q2, a
Q2, a  
 { { } }
ให้  (q, a) = (q, a) =  1(q, a)
ถ้า q 1(q, a)
ถ้า q  Q1 และ a Q1 และ a 
  {
{ } }
และ  (q, a) = (q, a) =  2(q, a)
ถ้า q 2(q, a)
ถ้า q  Q2 และ a Q2 และ a 
  {
{ } }
 (qF1, (qF1,  ) = {qF}
และ ) = {qF}
และ  (qF2, (qF2,  ) = {qF} ) = {qF}
- กรณีที่ r = r1r2, จากสมมติฐานการอุปนัยเราจะมี เครื่องออโตมาตาจำกัดเชิงไม่กำหนดสองเครื่อง
M1, M2 ที่ยอมรับ L(r1), L(r2) ตามลำดับและมีสถานะยอมรับเพียงสถานะเดียว
เราสร้างออโตมาตาเครื่องใหม่ M โดยมีสถานะเริ่มต้นและสถานะยอมรับใหม่ ดังรูป
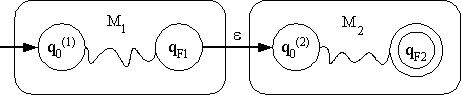
เราจะได้ว่า L(M) = L(M1)L(M2) = L(r1)L(r2) =
L(r1 r2) ตามที่ต้องการ
ในเชิงคณิตศาสตร์ เราเขียนอธิบายเครื่องออโตมาตา M ได้ดังนี้
- M1 = (Q1,
 , ,
 1, q0(1), {qF1}) และ M2 =
(Q2, 1, q0(1), {qF1}) และ M2 =
(Q2,  , ,  2,
q0(2), {qF2}) โดยที่สถานะทั้งสองเครื่องต่างกันทั้งหมด 2,
q0(2), {qF2}) โดยที่สถานะทั้งสองเครื่องต่างกันทั้งหมด
- ให้ M = (Q1
 Q2, Q2,
 , ,  , q0(1),
{qF2}) , q0(1),
{qF2})
- และนิยาม
 ดังนี้ ดังนี้
- สำหรับแต่ละ q
 Q1 Q1  Q2, a
Q2, a  
 { { }, },
ให้  (q, a) = (q, a) =  1(q, a)
ถ้า q 1(q, a)
ถ้า q  Q1 และ a Q1 และ a 
  {
{ } }
และ  (q, a) = (q, a) =
 2(q, a) ถ้า q 2(q, a) ถ้า q  Q2
และ a Q2
และ a  
 { { } }
-
 (qF1, (qF1,  ) =
{q0(2)} ) =
{q0(2)}
- กรณีที่ r = r1*, จากสมมติฐานการอุปนัยเราจะมี เครื่องออโตมาตาจำกัดเชิงไม่กำหนด
M1 ที่ยอมรับ L(r1) ซึ่งมีสถานะยอมรับเพียงสถานะเดียว
เราสร้างออโตมาตาเครื่องใหม่ M โดยมีสถานะเริ่มต้นและสถานะยอมรับใหม่ ดังรูป
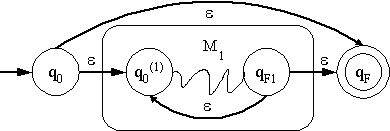
เราจะได้ว่า L(M) = L(M1)* = L(r1)* = L(r1*)
ตามที่ต้องการ
ในเชิงคณิตศาสตร์ เราเขียนอธิบายเครื่องออโตมาตา M ได้ดังนี้
- M1 = (Q1,
 , ,
 1, q0(1), {qF1}) 1, q0(1), {qF1})
- ให้ M = (Q1
 {q0, qF}, {q0, qF},
 , ,  , q0,
{qF}) โดยที่ q0 และ qF เป็นสถานะใหม่ที่ไม่ปรากฎใน Q1 , q0,
{qF}) โดยที่ q0 และ qF เป็นสถานะใหม่ที่ไม่ปรากฎใน Q1
- และนิยาม
 ดังนี้ ดังนี้
 (q0, (q0,  ) =
{q0(1), qF} และ ) =
{q0(1), qF} และ  (qF1, (qF1,
 ) = {q0(1), qF} ) = {q0(1), qF}
- สำหรับแต่ละ q
 Q1, a Q1, a 
  {
{ }, ให้ }, ให้  (q, a) = (q, a) =
 1(q, a) 1(q, a)
โดยอุปนัยเชิงคณิตศาสตร์ทำให้เราสรุปได้ว่า ไม่ว่านิพจน์ปกติที่มีจำนวนดำเนินการเท่าใด เราสามารถสร้างออโตมาตาจำกัดเชิงไม่กำหนด
ซึ่งยอมรับภาษาปกติของนิพจน์นั้นได้เสมอ
ตัวอย่าง 2
จงเขียนแผนภาพของออโตมาตาจำกัดที่ยอมรับ L(r) ตามการพิสูจน์ข้างต้นเมื่อ
- r = 00
- r = 1+00
- r = (1+00)*
- r = 01*+1
ทฤษฎีบท ถ้า L เป็นภาษาที่ยอมรับโดยออโตมาตาจำกัดเชิงกำหนดแล้วเราสามารถเขียนแทน L ด้วยนิพจน์ปกติได้
พิสูจน์ ให้ L เป็นภาษาที่ยอมรับโดยออโตมาตาจำกัดเชิงกำหนด M = ({q0, q1, ..., qn},
 , ,  , q0, F) , q0, F)
วิธีการพิสูจน์คือ เราขยายนิพจน์ปกติจากโครงแบบที่ไม่มีการวิ่งผ่านสถานะที่มีดรรชนีต่ำกว่าดรรชนีของสถานะที่กำลังพิจารณาอยู่
สำหรับแต่ละ i, j  {0, 1, 2, ..., n}, k {0, 1, 2, ..., n}, k
 {0, 1, 2, ..., n} {0, 1, 2, ..., n}
- ให้ Ri jk เป็นเซตของสายอักขระ x

 * ที่ (qi, x) * ที่ (qi, x)  (qj,
(qj,  )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k
ถ้าเราสามารถแสดงได้ว่า k ที่ได้เราสามารถเขียนนิพจน์ปกติขยายได้จนถึง n + 1 คำตอบของภาษาที่ต้องการจะได้จากยูเนียนของเซตที่แทนด้วย
นิพจน์ปกติจากเซตของ R0 jn+1 เมื่อ qj อยู่ใน F
เราใช้อุปนัยเข้มบน ดรรชนี k
มูลฐานของการอุปนัย จะแสดงว่าที่ k = 0 เราสามารถเขียนนิพจน์ปกติได้เสมอ
- ถ้า i
 j แล้ว Ri j0 = { a j แล้ว Ri j0 = { a 
 | |  (qi, a) = qj } (qi, a) = qj }
- ถ้า i = j แล้ว Ri j0 = { a
  |
|  (qi, a) = qj } (qi, a) = qj }  {
{ } }
จะเห็นได้ว่า Ri j0 เป็นเซตจำกัด ซึ่งเป็นสับเซตของ 
 { { } ดังนั้น } ดังนั้น
- Ri j0 =
 หรือ Ri j0 =
{ หรือ Ri j0 =
{ } หรือ Ri j0 = {a1, a2, ...,
am } } หรือ Ri j0 = {a1, a2, ...,
am }
เมื่อ a1, a2, ..., am 
  {
{ } }
ถ้าเราให้ ri j0 แทนนิพจน์ปกติที่เขียนแทน Ri j0 จะได้ว่า
- ri j0 =
 หรือ
ri j0 = หรือ
ri j0 =  หรือ ri j0 =
a1 + a2 + ... + am หรือ ri j0 =
a1 + a2 + ... + am
นั่นคือ Rij0 = L(ri j0)
ขั้นตอนของการอุปนัย เราตั้งสมมติฐานของการอุปนัยว่า เราสามารถเขียนนิพจน์ปกติสำหรับ Ri jk-1
x  Ri jk ก็ต่อเมื่อ Ri jk ก็ต่อเมื่อ
- (qi, x)
 (qj, (qj,  )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 (นั่นคือ x )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 (นั่นคือ x  Ri jk-1) Ri jk-1)
- หรือ x = w1w2w3 โดยที่ (qi, w1)
 (qk,
(qk,  ) โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 และ (qk, w2) ) โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 และ (qk, w2)
 (qk, (qk,  ) โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ
k-1 และ (qk, w3) ) โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ
k-1 และ (qk, w3)  (qj, (qj,  )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 ซึ่งมีความหมายตรงกับ )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 ซึ่งมีความหมายตรงกับ
- x
 Ri k-1k-1 (Rk-1 k-1k-1)*
Rk-1 jk-1 Ri k-1k-1 (Rk-1 k-1k-1)*
Rk-1 jk-1
นั่นคือทุก k  {0, 1, 2, ..., n, n+1} {0, 1, 2, ..., n, n+1}
- Ri jk = Ri k-1k-1 (Rk-1 k-1k-1)*
Rk-1 jk-1
 Ri jk-1 Ri jk-1
- หรือ x = w1w2(1)w2(2)...w2(n)w3
โดยที่ (qi, w1)
 (qk(1), (qk(1),
 ) โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 และ (qk(1),
w2(1)) ) โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 และ (qk(1),
w2(1))  (qk(2), (qk(2),
 ) จนกระทั่ง (qk(n-1), w2(n-1)) ) จนกระทั่ง (qk(n-1), w2(n-1))
 (qk(n), (qk(n),  )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 และ (qk(n), w3(n)) )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 และ (qk(n), w3(n))
 (qj, (qj,  )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 ซึ่งมีความหมายเดียวกับกรณีข้างต้น )
โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ k-1 ซึ่งมีความหมายเดียวกับกรณีข้างต้น
จากสมมติฐานของการอุปนัย Rs tk-1 สามารถเขียนแทนด้วยนิพจน์ปกติ rs tk-1
ดังนั้นเราเขียนนิพจน์ปกติได้ดังนี้
- ri jk = (ri k-1k-1) (rk-1 k-1k-1)*
rk-1 jk-1 + ri jk-1 แทน Ri jk
โดยอุปนัยเชิงคณิตศาสตร์ เราสามารถเขียนแทน Ri j0, Ri j1, ..., Ri jn, Ri jn+1
ด้วยนิพจน์ปกติได้เสมอ
ขั้นต่อไป เราจะแสดงว่า  R0 jn+1 = L โดยเราทราบว่า R0 jn+1 = L โดยเราทราบว่า
- R0 jn+1 = {x

 * | (q0, x) * | (q0, x)  (qj,
(qj,  ) โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ n+1 } = {x ) โดยไม่ผ่านสถานะที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ n+1 } = {x
  * | (q0, x) * | (q0, x)
 (qj, (qj,  )}
เพราะไม่มีสถานะใด ๆ ที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ n+1 ได้ )}
เพราะไม่มีสถานะใด ๆ ที่มีดรรชนีล่างใหญ่กว่าหรือเท่ากับ n+1 ได้
- สมมติ x
 R1 jn+1 โดยที่ qj R1 jn+1 โดยที่ qj
 F จะได้ว่า (q1, x) F จะได้ว่า (q1, x)  (qj,
(qj,  ) และ qj ) และ qj  F
นั่นคือ x F
นั่นคือ x  L(M) = L L(M) = L
- สมมติว่า x
 L = L(M) จะมี qm L = L(M) จะมี qm
 F ซึ่ง (q0, x) F ซึ่ง (q0, x)  (qm,
(qm,  ) นั่นคือ x ) นั่นคือ x  R0mn และ qm
R0mn และ qm  F ได้ว่า x F ได้ว่า x
  R0 jn+1 R0 jn+1
- L = L(M) =
 R0 jn+1 R0 jn+1
เราสามารถเขียน L(M) ด้วยนิพจน์ปกติได้
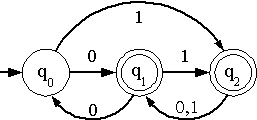
ตัวอย่าง 3 จงหานิพจน์ปกติที่เป็นสัญลักษณ์แทน L(M) เมื่อให้ M เป็นออโตมาตาจำกัดเชิงกำหนด
ที่มีแผนภาพข้างล่าง
ทฤษฎีบทตั้งการปั๊มขึ้นมาของออโตมาตาจำกัด (Pumping lemma for FAs)
ถ้า L เป็นภาษาปกติแล้วจะได้ว่ามี k 
 ที่ ที่
(*) สำหรับทุก x   *
ถ้า x *
ถ้า x  L และ |x| L และ |x|
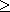 k แล้ว x = ywz โดยที่ 1 k แล้ว x = ywz โดยที่ 1  |w|,
|yw| |w|,
|yw|  k และ ywiz k และ ywiz  L
ทุก i L
ทุก i   0 0
ตัวอย่าง 4 จงพิสูจน์ว่า {0n×n | n 
 } ไม่เป็นภาษาปกติโดยใช้ทฤษฎีบทตั้งการปั๊มขึ้นมาของออโตมาตาจำกัด } ไม่เป็นภาษาปกติโดยใช้ทฤษฎีบทตั้งการปั๊มขึ้นมาของออโตมาตาจำกัด
พิสูจน์ กำหนดให้  = {0, 1}
และ ให้ L = {0n×n | n = {0, 1}
และ ให้ L = {0n×n | n   } }
จะแสดงการพิสูจน์ว่า L ไม่เป็นภาษาปกติโดยวิธีการขัดแย้ง จึงสมมติว่า L เป็นภาษาปกติ
โดยทฤษฎีบทตั้งการปั๊มขึ้นมาของออโตมาตาจำกัดจะได้ว่า มีจำนวนเต็มบวก k ที่สอดคล้องกับสมบัติ (*)
พิจารณา x = 0k×k จะได้ว่า x  L และ |x| = k×k = k2
ซึ่งมากกว่าหรือเท่ากับ k L และ |x| = k×k = k2
ซึ่งมากกว่าหรือเท่ากับ k
เราเขียน 0k×k = ywz โดยที่ 1  |w|, |yw| |w|, |yw|
 k และ ywiz k และ ywiz  L
ทุกจำนวนเต็ม i L
ทุกจำนวนเต็ม i 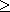 0 0
ถ้าพิจารณาที่ i = 2 จะได้ว่า ywwz  L จาก (*) เมื่อเรานับจำนวนอักขระของ ywwz L จาก (*) เมื่อเรานับจำนวนอักขระของ ywwz
- |ywwz| > k2 เพราะ |w|
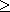 1 และ |ywz| = k2 1 และ |ywz| = k2
- |ywwz|
 k2 + k เพราะ |yw| k2 + k เพราะ |yw|
 k และ |ywwz| k และ |ywwz|  k + |wz| k + |wz|
 k + k2 = k(k+1) < (k+1)2 k + k2 = k(k+1) < (k+1)2
กล่าวคือ
- k2 < | ywwz | < (k+1)2
ซึ่งได้ว่าขนาดของ ywwz ไม่ใช่กำลังสองสมบูรณ์ของเลขจำนวนเต็มใด ๆ นั่นคือ ywwz ไม่อยู่ใน L เกิดการขัดแย้ง
ที่สมมติไว้ไม่เป็นจริง ดังนั้น L ไม่เป็นภาษาปกติ
ตัวอย่าง 5 จงพิสูจน์ว่า {02n1n | n
  } ไม่เป็นภาษาปกติ } ไม่เป็นภาษาปกติ
พิสูจน์ กำหนดให้  = {0, 1}
และ ให้ L = {02n1n | n = {0, 1}
และ ให้ L = {02n1n | n   } }
จะแสดงการพิสูจน์ว่า L ไม่เป็นภาษาปกติโดยวิธีการขัดแย้ง จึงสมมติว่า L เป็นภาษาปกติ
โดยทฤษฎีบทตั้งการปั๊มขึ้นมาของออโตมาตาจำกัดจะได้ว่า มีจำนวนเต็มบวก k ที่สอดคล้องกับสมบัติ (*)
พิจารณา x = 02k1k จะได้ว่า x  L และ |x| = 2 k + k = 3 k
ซึ่งมากกว่าหรือเท่ากับ k L และ |x| = 2 k + k = 3 k
ซึ่งมากกว่าหรือเท่ากับ k
เราเขียน 02k1k = ywz โดยที่ 1  |w|, |yw| |w|, |yw|
 k และ ywiz k และ ywiz  L
ทุกจำนวนเต็ม i L
ทุกจำนวนเต็ม i 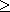 0 กล่าวคือ ywwz 0 กล่าวคือ ywwz  L L
เนื่องจาก | yw |  k และ ywz = 02k1k เราได้ว่า k และ ywz = 02k1k เราได้ว่า
- y = 0j และ w = 0i สำหรับบางค่าของ i
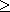 1 และ
j 1 และ
j 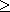 0 0
การที่เราทราบว่า ywwz อยู่ใน L และ ywwz = 02k+i1k เราต้องได้ว่า 2k + i = 2k นั่นคือ i = 0 เกิดขัดแย้ง
ที่สมมติไว้ไม่เป็นจริง ดังนั้น L ไม่เป็นภาษาปกติ
ตัวอย่าง 6 จงตรวจสอบว่าภาษาใด ในข้อต่อไปนี้เป็นภาษาปกติพร้อมแสดงการพิสูจน์
- L1 = {0n1n | n

 } }
- L2 = {0n1m | m, n

 0} 0}
- L3 = {1n20n | n

 0} 0}
- L4 = {02n | n

 } }
- L5 = {0n1m | n, m

 } }
- L6 = {1n×n×n | n

 } }
- L7 = {wwR | w
 {0,1}*} {0,1}*}
- L8 = {ww | w
 {0,1}*} {0,1}*}
- L9 = {www | w
 {0,1}*} {0,1}*}
- L10 = {0n1m | n
 m} m}
- L11 = {1n0m | n < m}
- L12 = {1n02n1m | n < m}
|