ขณะนี้ เรารู้จักออโตมาตาจำกัดทั้งสามชนิดแล้วคือ ออโตมาตาจำกัดเชิงกำหนด ออโตมาตาจำกัดเชิงไม่กำหนด และออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้าย- เราต้องการทราบว่า ออโตมาตาทั้งสามแบบ มีความสามารถในการยอมรับภาษาต่างกันหรือไม่ โดยพิจารณาการสมมูลกันของออโตมาตาทั้งสามแบบ
บทนิยาม ให้ M และ M' เป็นออโตมาตาจำกัดสองเครื่องใด ๆ เรากล่าวว่า M สมมูล (equivalent) กับ M' ก็ต่อเมื่อ L(M) = L(M')
ต่อไปเราจะแสดงว่าความสามารถในการยอมรับภาษาของเครื่องออโตมาตาทั้งสามแบบเหมือนกัน
ทฤษฎีบทการสมมูลกันของออโตมาตาจำกัดเชิงกำหนดกับออโตมาตาจำกัดเชิงไม่กำหนด

1. สำหรับออโตมาตาจำกัดเชิงกำหนด M เราสามารถสร้างออโตมาตาจำกัดเชิงไม่กำหนด M' ที่สมมูลกับ M ได้
2. สำหรับออโตมาตาจำกัดเชิงไม่กำหนด M' เราสามารถสร้างออโตมาตาจำกัดเชิงกำหนด M ที่สมมูลกับ M' ได้

พิสูจน์

1. กำหนดให้ M = (Q, , , q₀, F) เป็นออโตมาตาจำกัดเชิงกำหนดเครื่องหนึ่ง เราสร้างออโตมาตาจำกัดเชิงไม่กำหนดให้เหมือนกับ M โดยเปลี่ยนนิยาม เป็น ' ใหม่ดังนี้
   สร้าง M' = (Q, , ', q₀, F) และ ': Q × 2^Q โดยที่

   สำหรับแต่ละ q Q, a , '(q, a) = {(q, a)}

   เราจะแสดงได้ง่ายว่า L(M) = L(M')
2. กำหนดให้ M' = (Q, , ', q₀, F') เป็นออโตมาตาจำกัดเชิงไม่กำหนดเครื่องหนึ่ง เราสร้างออโตมาตาจำกัดเชิงกำหนด โดยนิยามสถานะใหม่ให้เป็นเซตของสถานะแทนที่จะเป็นสถานะเดี่ยวดังนี้
   สร้าง M = (2^Q, , , {q₀}, F) และ : 2^Q × 2^Q โดยที่
   • 2^Q หมายถึงเซตของทุกสับเซตทั้งหมดที่เป็นไปได้ของ Q นั่นคือ 2^Q = { A | A Q }
   • F = { A | A Q และ A F' }
   • สำหรับแต่ละ S 2^Q และ a , ให้ (S, a) = '(q, a)
   เราจะแสดงว่า L(M') = L(M) โดยแสดงว่า L(M') L(M) และ L(M) L(M')
   1. ให้ w L(M') จะได้ว่า '(q₀, w) F'

      ถ้า w = จะได้ว่า q₀ F' หมายความว่า {q₀} 2^Q และ {q₀} F' โดยนิยามการเป็นสมาชิกของเซต F เราได้ว่า {q₀} F
      กล่าวคือ w = L(M)

      ถ้า w จะได้ w = a₁...a_n โดยที่ a_i เนื่องจาก w L(M') จะมีสถานะ q₁, ..., q_n Q โดยที่ q_n F' และ (q₀, a₁a₂...a_n ) (q₁, a₂...a_n ) ... (q_n, )
      จะได้ว่า q₁ '(q₀, a₁) แทนด้วย A₁,
      q₂ '(q₁, a₂) แทนด้วย A₂
      ... q_n '(q_n-1, a_n) แทนด้วย A_n ซึ่งเป็นสับเซตของ Q
      เราพบว่าสถานะร่วมระหว่าง F' กับ A_n คือ q_n ดังนั้น A_n F จากนิยามของ ที่ขยายมาจาก สำหรับ A₁, ..., A_n
      ({q₀}, a₁) = '(q₀, a₁) = A₁
      (A₁, a₂) = A₂
      ... (A_n-1, a_n) = A_n
      สรุปได้ว่า ({q₀}, w) = ({q₀}, a₁a₂...a_n) (A_n, )
      จะได้ว่า M ยอมรับ w นั่นคือ L(M') L(M)

   2. ให้ w L(M)

      ถ้า w = จะได้ว่า ({q₀}, w) ({q₀}, ) จะได้ว่า {q₀} F จากนิยาม {q₀} F' เราต้องได้ว่า q₀ F' สรุปได้ว่า w = L(M')

      ถ้า w จะได้ w = a₁...a_n โดยที่ a_i เนื่องจาก w L(M) จะมีสถานะ A₁, ..., A_n 2^Q โดยที่ A_n F และ ({q₀}, a₁a₂...a_n ) (A₁, a₂...a_n ) ... (A_n, )
      นั่นคือ A_n Q และ A_n F'
      เราสามารถเลือกสถานะ q₁ A₁, ... , q_n A_n ได้ที่ทำให้การแปลงสุดท้ายได้ q_n F'
      สรุปได้ว่า (q₀, w) = (q₀, a₁a₂...a_n) (q_n, ) โดยที่ q_n F'
      จะได้ว่า M' ยอมรับ w นั่นคือ L(M) L(M')

จบการพิสูจน์

เราได้ว่ากลุ่มของภาษาที่ยอมรับโดยออโตมาตาจำกัดเชิงกำหนด กับกลุ่มของภาษาออโตมาตาจำกัดเชิงไม่กำหนดเป็นกลุ่มเดียวกัน
ตัวอย่างที่ 1 กำหนด M' = (Q', , , q₀, F') โดยที่ Q' = {q₀, q₁}, = {0, 1} และ F' = {q₁} เป็นออโตมาตาจำกัดเชิงไม่กำหนดเครื่องหนึ่ง ที่มีฟังก์ชันการผ่าน นิยามดังนี้

	0	1
q0	{q0, q1}	{q1}
q1		{q0, q1}

จงสร้างออโตมาตาจำกัดเชิงกำหนด M' ที่สมมูลกับ M โดยใช้วิธีการสร้างจากการพิสูจน์ของทฤษฎีบทการสมมูลกัน ของออโตมาตาจำกัดเชิงกำหนดกับออโตมาตาจำกัดเชิงไม่กำหนด
ทฤษฎีบทการสมมูลกันของออโตมาตาจำกัดเชิงไม่กำหนดกับออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้าย-

1. สำหรับออโตมาตาจำกัดเชิงไม่กำหนด M เราสามารถสร้าง ออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้าย- M' ที่สมมูลกับ M ได้
2. สำหรับออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้าย- M' เราสามารถสร้างออโตมาตาจำกัดเชิงไม่กำหนด M ที่สมมูลกับ M' ได้

พิสูจน์

• กำหนดให้ M = (Q, , , q₀, F) เป็นออโตมาตาจำกัดเชิงไม่กำหนดเครื่องหนึ่ง เราสร้างออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้าย- ให้เหมือนกับ M โดยเปลี่ยนนิยาม เป็น ' ใหม่ดังนี้
  สร้าง M' = (Q, , ', q₀, F) และ ': Q × ( {}) 2^Q โดยที่

  สำหรับแต่ละ q Q, a , '(q, a) = (q, a) และ '(q, ) = {q}

  เราจะแสดงได้ง่ายว่า L(M) = L(M') และแผนภาพการผ่านของทั้งสองเครื่องจะเหมือนกัน
• กำหนดให้ M' = (Q', , ', q₀, F') เป็นออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้าย- เครื่องหนึ่ง เราสร้างออโตมาตาจำกัดเชิงไม่กำหนดที่ไม่มีการย้าย พิจารณาว่า q₀ ควรเป็นสถานะยอมรับหรือไม่ และกำจัดอาร์กที่มี กำกับอยู่โดยการเขียนอาร์กใหม่ดังนี้
  M = (Q', , , q₀, F) โดยที่

  ถ้า -CL(q₀) F' แล้ว ให้ F = F' {q₀}

  ถ้า -CL(q₀) F' = แล้ว ให้ F = F'

  และสำหรับแต่ละ p Q', a , S = -CL(p), ให้ (p, a) = '(q, a)

  เราจะแสดงว่า L(M') = L(M) โดยจะใช้แสดงว่า
  1. ทุก w ^*, ถ้า w แล้ว (q₀, w) = '(q₀, w)
  2. ทุก w ^*, (q₀, w) F ก็ต่อเมื่อ '(q₀, w) F'

• ให้ w ^*, โดยที่ w จะใช้ อุปนัยเข้มบน | w |
  มูลฐานของการอุปนัย | w | = 1ได้ว่า w = a , (q₀, a) = '(q₀, a) และ '(q₀, a) = '(q₀, a) จึงได้ว่า (q₀, a) = (q₀, a) โดยพิจารณานิยามการขยายของ (q₀, a) = '(q₀, a)
  สมมติฐานของการอุปนัย สมมติว่า | w | > 1 และทุก x ^* ที่ | x | < | w | ถ้า x แล้ว (q₀, x) = '(q₀, x)
  ต้องการแสดงว่า (q₀, w) = '(q₀, w)
  จาก | w | > 1 เขียน w = xa โดยที่ | x | > 0 และ a จากสมมติฐานของการอุปนัยได้ (q₀, x) = '(q₀, x) = {p₁, ..., p_m}
  พิจารณา (q₀, w) = (q₀, xa) = (p₁, a) ... (p_m, a) = '(p₁, a) ... '(p_m, a) = '(q₀, xa) = '(q₀, w)
• ให้ w ^*, สมมติว่า '(q₀, w) F'

  ถ้า w = จะได้ว่า '(q₀, w) = '(q₀, ) = {q₀} จึงได้ q₀ F' ซึ่งจากนิยามของ F' เราอาจได้ q₀ F หรือ q₀ -CL(q₀) F นำไปสู่ข้อสรุป (q₀, w) F
  สมมติว่า w จะได้ w = xa สำหรับบาง x ^* และ a และ '(q₀, w) = (q₀, w)
  รวมกับสมมติฐานข้างต้นได้ว่า

  (q₀, w) F'

  F' = F {q₀}
  จะพิสูจน์โดยการขัดแย้ง ต้องการ (q₀, w) F สมมติว่าไม่จริงนั่นคือ (q₀, w) F = เราได้ว่า q₀ ไม่อยู่ใน F และ q₀ อยู่ใน (q₀, w) ดังนั้น -CL(q₀) F จะมี p -CL(q₀) F และจาก w = xa q₀ อยู่ใน (q₀, w) จะได้ว่า p -CL(S) เมื่อ S คือยูเนียนของ (q, a) เมื่อ q เป็นสถานะที่ได้จาก q₀ อ่าน x
  p (q₀, w) F ซึ่งขัดแย้งกับที่สมมติว่า (q₀, w) F = ที่สมมติไว้ไม่จริง
  ในทางกลับกัน สมมติว่า (q₀, w) F
  ถ้า w = จะได้ว่า (q₀, w) = -CL(q₀) และ '(q₀, w) = {q₀} จากนิยามของ F' จะได้ F' = F {q₀} และ '(q₀, w) F'
  สมมติว่า w จะได้ '(q₀, w) = (q₀, w) และ F F' และ '(q₀, w) F'

จบการพิสูจน์

เราได้ว่ากลุ่มของภาษาที่ยอมรับโดยออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้าย- กับกลุ่มของภาษาออโตมาตาจำกัดเชิงไม่กำหนดเป็นกลุ่มเดียวกัน
ตัวอย่างที่ 2 กำหนด M = (Q, , , q₀, F) เป็น ออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้าย- ที่มีแผนภาพการผ่านดังรูป

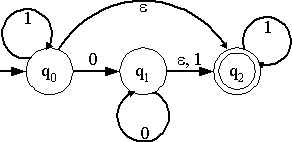
จงสร้างออโตมาตาจำกัดเชิงไม่กำหนด M' ที่สมมูลกับ M โดยใช้วิธีการสร้างจากการพิสูจน์ของทฤษฎีบทการสมมูลกัน ของออโตมาตาจำกัดเชิงไม่กำหนดกับออโตมาตาจำกัดเชิงไม่กำหนดที่มีการย้าย-

ทฤษฎีบท สมบัติของภาษาปกติ
ถ้า R ₁ และ S ₂ เป็นภาษาปกติแล้ว R S, RS, R^*, ^* - R, R S เป็นภาษาปกติทั้งสิ้น
พิสูจน์ R S, RS, R^*, เป็นภาษาปกติ (ชัดเจนจากนิยาม ของภาษาปกติ)

• สำหรับ ^* - R เราทำดังนี้ จาก R เป็นภาษาปกติจะมีออโตมาตาจำกัดเชิงกำหนด M = (Q, , , q₀, F) ที่ยอมรับ R
  สร้างออโตมาตาจำกัด M' = (Q, , , q₀, F') ที่ยอมรับ ^* - R โดยปรับสถานะยอมรับเป็นสถานะปฏิเสธและ สถานะปฏิเสธเป็นสถานะยอมรับโดยที่ทุกสถานะต้องมีอาร์กที่มีสัญลักษณ์ใน ออกมาทุกตัว นั่นคือ F' = Q - F
  เราจะได้ว่า L(M') = ^* - R นั่นคือ ^* - R เป็นภาษาที่ยอมรับโดยออโตมาตาจำกัดเชิงกำหนด
  เราเขียนแทน ^* - R ด้วยนิพจน์ปกติได้
• สำหรับ R S ที่ R ^* และ S ^*, เราทำดังนี้ จาก R เป็นภาษาปกติจะมีออโตมาตาจำกัดเชิงกำหนด M₁ = (Q₁, , ₁, q⁽¹⁾₀, F₁) ที่ยอมรับ R
  จาก S เป็นภาษาปกติจะมีออโตมาตาจำกัดเชิงกำหนด M₂ = (Q₂, , ₂, q⁽²⁾₀, F₂) ที่ยอมรับ S
  สร้างออโตมาตา M = (Q, , , q₀, F) ที่ยอมรับ R S ได้ดังนี้
  ให้ Q = Q₁ × Q₂, q₀ = (q⁽¹⁾₀, q⁽²⁾₀), F = F₁ × F₂
  สำหรับทุก (p, q) Q₁ × Q₂ และทุก a , ((p,q), a) = (₁(p,a), ₂(q,a))
  (หมายเหตุ ถ้า ₁(p,a) ไม่มีค่าหรือ ₂(q,a) ไม่มีค่าแล้ว ((p,q),a) ไม่มีค่าด้วย)
  จะได้ว่า L(M) = R S นั่นคือ R S เป็นภาษาที่ยอมรับโดยออโตมาตาจำกัดเชิงกำหนด ดังนั้น เราเขียนแทน R S ด้วยนิพจน์ปกติได้