เครื่องหรืออุปกรณ์ที่เรานิยามโดยใช้ ออโตมาตาจำกัดทั้งสามชนิดมีความสามารถในการยอมรับภาษาที่เหมือนกัน และ เรายังพบว่าภาษาที่เครื่องทั้งสามยอมรับนั้นเป็นเพียงภาษาปกติ ต่อไปเราจะแนะนำเครื่องออโตมาตาที่มีความสามารถยอมรับภาษาได้มากกว่าภาษาปกตินั่นคือ ออโตมาตาแบบกดลงเชิงกำหนด และออโตมาตาแบบกดลงเชิงไม่กำหนด
เราพิจารณาว่าออโตมาตาแบบกดลงเชิงกำหนดเป็นเครื่องที่มี แถบบันทึกรับเข้า และตัวควบคุมจำกัดเหมือนออโตมาตาจำกัด แต่มีหน่วยความจำเพิ่มเติมขึ้นมาคือ หน่วยความจำช่วยแบบกองซ้อน ดังรูป

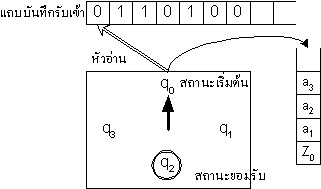
ตัวควบคุมจำกัดจะอยู่ในสถานะใดสถานะหนึ่ง อ่านสัญลักษณ์ที่ปรากฎบนแถบบันทึกรับเข้าผ่านหัวอ่าน และดึงสัญลักษณ์ในกองซ้อนออก โดยดึงเฉพาะตัวที่อยู่บนสุดเท่านั้น เมื่ออ่านเสร็จแล้วตัวควบคุมจำกัดอาจย้ายไปอยู่ในสถานะอื่นหรือคงอยู่สถานะเดิมก็ได้ หัวอ่านของแถบบันทึกรับเข้า จะเคลื่อนขวา 1 เซล แล้วเติมสัญลักษณ์ซ้อนทับลงไปหรืออาจไม่เติมสัญลักษณ์ใด ๆ ลงไปบนกองซ้อน ซึ่งการเติมสัญลักษณ์ในกองซ้อนทับลงไปอาจเติม ได้มากกว่า 1 ตัวในแต่ละครั้ง
บทนิยาม ออโตมาตากดลงเชิงกำหนด (Deterministic Pushdown Automata) หรือเรียกสั้นๆ ว่า ดีพีดีเอ (DPDA) แต่ละเครื่องประกอบด้วย

1. Q แทนเซตของสถานะจำกัด (the set of states)
2. แทนเซตของสัญลักษณ์รับเข้าทั้งหมดที่เป็นไปได้ซึ่งเป็นเซตจำกัด (the set of input symbols)
3. q₀ แทนสถานะเริ่มต้น (the initial state)
4. F แทนเซตของสถานะยอมรับ (the set of accepting state)
5. แทนเซตของสัญลักษณ์กองซ้อนทั้งหมดซึ่งเป็นเซตจำกัด (the set of stack symbols)
6. Z₀ แทนสัญลักษณ์เริ่มต้นของกองซ้อน ซึ่งเป็นสมาชิกของ ปรากฎที่ตำแหน่งล่างสุดของกองซ้อนเท่านั้น (the initial stack symbol)
7. แทนฟังก์ชันการผ่าน (transition function) ที่มีโดเมนเป็นสับเซตของ Q × ( {}) × และพิสัยเป็นสับเซตของ Q × ^* เขียนแทนด้วย

   :_partial Q × ( {}) × 2^{Q × *}

   และมีเงื่อนไขว่า สำหรับแต่ละ q Q, a , A ,

   (q, a, A) ต้องมีการเปลี่ยนสถานะเพียงหนึ่งเดียว

   และถ้า (p, ) (q, , A) แล้ว (q, a, A) ต้องไม่มีการเปลี่ยนสถานะไปเป็นสถานะอื่นสำหรับทุก a .

จะใช้สัญลักษณ์ (Q, , , , q₀, Z₀, F) แทนออโตมาตากดลงเชิงกำหนดเครื่องหนึ่ง
บทนิยามแผนภาพการผ่าน (transition diagram) ของออโตมาตากดลงเชิงกำหนด (Q, , , , q₀, Z₀, F) เครื่องหนึ่งคือ กราฟเทียมที่มีทิศทางโดย

1. มี Q เป็นเซตของจุดยอดทั้งหมด และมีลูกศรชี้เข้าที่จุดยอด q₀
2. มีวงกลมสองวงล้อมรอบจุดยอดทุกจุดใน F และ
3. มีอาร์กเชื่อมจากจุดยอด p ไปจุดยอด q โดยมีสัญลักษณ์ a, A/ เขียนกำกับอยู่ ก็ต่อเมื่อ (q, ) (p, a, A) โดยที่ a , A และ ^*

ตัวอย่างที่ 1 จงเขียนแผนภาพการผ่านของออโตมาตากดลงเชิงกำหนด M = (Q, , , , q₀, Z₀, F) ที่มี Q = {q₀, q₁, q₂}, F = {q₂}, = {0, 1}, = {0, 1, Z₀} และ นิยามดังนี้

(q₀, 0, Z₀) = {(q₀, 00Z₀)}, (q₀, 0, 0) = {(q₀, 000)}, (q₀, 1, 0) = {(q₁, )}

(q₁, 1, 0) = {(q₁, )}, (q₁, , Z₀) = {(q₂, )}

ตัวอย่างที่ 2 จงอธิบายการทำงานของออโตมาตากดลงเชิงกำหนดที่กำหนดให้

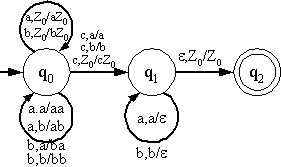
นิยาม โครงแบบ (Configuration) ของออโตมาตากดลงเชิงกำหนด
กำหนด M = (Q, , , , q₀, Z₀, F) คือสามสิ่งอันดับ (q, x, ) Q × ^* × ^* ซึ่งหมายถึงในขณะนั้น M อยู่ในสถานะ q และหัวอ่านอยู่ที่สัญลักษณ์ตัวแรกสุดทางซ้ายของ x และ เป็นข้อมูลในกองซ้อน โดยสัญลักษณ์ซ้ายสุดคือตัวบนสุดของกองซ้อน เช่น (q₀, 0110100, a₃a₂a₁Z₀) เป็นโครงแบบของออโตมาตากดลงเชิงกำหนดจากรูปแรก
เราเปลี่ยนโครงแบบได้โดยใช้กฎดังนี้

1. (q₁, x₁, ₁) เป็น โครงแบบถัดจาก (q, x, ) เขียนแทนด้วย (q, x, ) (q₁, x₁, ₁) ก็ต่อเมื่อ มี a , x₁ ^*, A และ , ^* ที่ทำให้
   1. x = a x₁, = A , ₁ = และ (q, a, A) = {(q₁, )}
   2. x = x₁, = A , ₁ = และ (q, , A) = {(q₁, )}
2. โครงแบบ (q', x', ') เป็น โครงแบบที่ได้มาจาก (q, x, ) เขียนแทนด้วยสัญลักษณ์ (q, x, ) (q', x', ') ก็ต่อเมื่อ (q, x, ) = (q', x', ') หรือมีโครงแบบ c₁, c₂, ..., c_n ที่มีสมบัติว่า c₁ = (q, x, ), c_n = (q', x', ') และ c₁ c₂ . . . c_n-1 c_n

M ยอมรับ w ก็ต่อเมื่อ มี q F ที่ทำให้ (q₀, w, Z₀) (q, , ) เมื่อ ^* ในกรณีนี้เราเรียก (q₀, w, Z₀) ว่า โครงแบบเริ่มต้น (initial configuration) และ (q, , ) ว่า โครงแบบยอมรับ (accepting configuration) และ ภาษาที่ M ยอมรับ เขียนแทนด้วย L(M) คือ { w ^* | M ยอมรับ w} ดังนั้นภาษา L ใด ๆ จะเป็นภาษาที่ M ยอมรับ ก็ต่อเมื่อ L = L(M)
ตัวอย่างที่ 3 จงพิจารณาว่าประโยคต่อไปนี้ยอมรับโดยเครื่องออโตมาตากดลงเชิงกำหนดที่กำหนดให้ใน ตัวอย่างที่ 1 หรือไม่

1. 
2. 0
3. 1
4. 011
5. 0011
6. 001111

ตัวอย่างที่ 4 จงพิจารณาว่าประโยคต่อไปนี้ยอมรับโดยเครื่องออโตมาตากดลงเชิงกำหนดที่กำหนดให้ในตัวอย่างที่ 2 หรือไม่ พร้อมสรุปภาษาที่ออโตมาตาเครื่องนี้ยอมรับ

1. 
2. a
3. ab
4. aa
5. bb

ตัวอย่างที่ 5 จงสร้างออโตมาตากดลงเชิงกำหนดที่ยอมรับ L = {w2w^R | w {0, 1}^*}
ตัวอย่างที่ 6 จงสร้างออโตมาตากดลงเชิงกำหนดที่ยอมรับ L = {0, 1}^*
ตัวอย่างที่ 7 จงสร้างออโตมาตากดลงเชิงกำหนดที่ยอมรับ L = {w {0, 1}^* | n(0, w) = n(1, w)}

ออโตมาตาแบบกดลงเชิงไม่กำหนด
บทนิยาม ออโตมาตากดลงเชิงไม่กำหนด (Nondeterministic pushdown automata) หรือเรียกสั้นๆ ว่า เอ็นพีดีเอ (NPDA) แต่ละเครื่องประกอบด้วย

1. Q แทนเซตของสถานะจำกัด (the set of states)
2. แทนเซตของสัญลักษณ์รับเข้าทั้งหมดที่เป็นไปได้ซึ่งเป็นเซตจำกัด (the set of input symbols)
3. q₀ แทนสถานะเริ่มต้น (the initial state)
4. F แทนเซตของสถานะยอมรับ (the set of accepting state)
5. แทนเซตของสัญลักษณ์กองซ้อนทั้งหมดซึ่งเป็นเซตจำกัด (the set of stack symbols)
6. Z₀ แทนสัญลักษณ์เริ่มต้นของกองซ้อน ซึ่งเป็นสมาชิกของ ปรากฎที่ตำแหน่งล่างสุดของกองซ้อนเท่านั้น (the initial stack symbol)
7. แทนฟังก์ชันการผ่าน (transition function) ที่มีโดเมนเป็นสับเซตของ Q × ( {}) × และพิสัยเป็นสับเซตของ Q × ^* เขียนแทนด้วย

   :_partial Q × ( {}) × 2^{Q × *}

   โดยไม่มีเงื่อนไขอื่นเพิ่มเติม เราจะใช้สัญลักษณ์ (Q, ,  , , q₀, Z₀, F) แทนออโตมาตากดลงเชิงไม่กำหนดเครื่องหนึ่ง

บทนิยามแผนภาพการผ่านของออโตมาตากดลงเชิงไม่กำหนดเหมือนกับของออโตมาตากดลงเชิงกำหนดคือ กราฟเทียมที่มีทิศทางโดย

1. มี Q เป็นเซตของจุดยอดทั้งหมด และมีลูกศรชี้เข้าที่จุดยอด q₀
2. มีวงกลมสองวงล้อมรอบจุดยอดทุกจุดใน F และ
3. มีอาร์กเชื่อมจากจุดยอด p ไปจุดยอด q โดยมีสัญลักษณ์ a, A/ เขียนกำกับอยู่ ก็ต่อเมื่อ (q, ) (p, a, A) โดยที่ a , A และ ^*

นิยาม โครงแบบ (Configuration) ของออโตมาตากดลงเชิงไม่กำหนด
กำหนด M = (Q, , , , q₀, Z₀, F) คือสามสิ่งอันดับ (q, x, ) Q × ^* × ^* ซึ่งหมายถึงในขณะนั้น M อยู่ในสถานะ q และหัวอ่านอยู่ที่สัญลักษณ์ตัวแรกสุดทางซ้ายของ x และ เป็นข้อมูลในกองซ้อน โดยสัญลักษณ์ซ้ายสุดคือตัวบนสุดของกองซ้อน
เราเปลี่ยนโครงแบบได้โดยใช้กฎดังนี้

1. (q₁, x₁, ₁) เป็น โครงแบบถัดจาก (q, x, ) เขียนแทนด้วย (q, x, ) (q₁, x₁, ₁) ก็ต่อเมื่อ มี a , x₁ ^*, A , , ^* ที่ทำให้
   1. x = a x₁, = A , ₁ = และ (q₁, ) (q, a, A)
   2. x = x₁, = A , ₁ = และ (q₁, ) (q, , A)
2. โครงแบบ (q', x', ') เป็น โครงแบบที่ได้มาจาก (q, x, ) เขียนแทนด้วยสัญลักษณ์ (q, x, ) (q', x', ') ก็ต่อเมื่อ (q, x, ) = (q', x', ') หรือมีโครงแบบ c₁, c₂, ..., c_n ที่มีสมบัติว่า c₁ = (q, x, ), c_n = (q', x', ') และ c₁ c₂ . . . c_n-1 c_n

M ยอมรับ สายอักขระรับเข้า w ก็ต่อเมื่อ มี q F ที่ทำให้ (q₀, w, Z₀) (q, , ) เมื่อ ^* และ ภาษาที่ M ยอมรับ เขียนแทนด้วย L(M) คือ { w ^* | M ยอมรับ w} ดังนั้นภาษา L ใด ๆ จะเป็นภาษาที่ M ยอมรับ ก็ต่อเมื่อ L = L(M)
ตัวอย่างที่ 8 จงสร้างออโตมาตากดลงเชิงไม่กำหนดที่ยอมรับ L = {ww^R | w {0,1}^* }
ตัวอย่างที่ 9 จงสร้างออโตมาตากดลงเชิงไม่กำหนดที่ยอมรับ L = {x {0,1}^* | x = x^R}
ตัวอย่างที่ 10 จงสร้างออโตมาตากดลงเชิงไม่กำหนดที่ยอมรับ L = {w {0,1}^* | 2n(1, w) = n(0, w)}

ออโตมาตาแบบกดลงที่ยอมรับโดยกองซ้อนว่าง
บทนิยาม ออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่าง คือเครื่องออโตมาตากดลงที่อาจเป็นดีพีดีเอหรือเอ็นพีดีเอ ก็ได้ที่มีการนิยามสถานะยอมรับใหม่ดังนี้

M ยอมรับ w โดยกองซ้อนว่าง (accept by empty stack) ก็ต่อเมื่อมี p Q ที่ทำให้ (q₀, w, Z₀) (p, , ) และภาษาที่ M ยอมรับโดยกองซ้อนว่าง เขียนแทนด้วย N(M) คือ { w ^* | M ยอมรับ w โดยกองซ้อนว่าง}

เราสามารถแสดงได้ว่า ออโตมาตากดลงแบบปกติ มีความสามารถเหมือนกับ ออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่าง
หมายเหตุ

• ภาษาที่ M ยอมรับ อาจเรียกอีกแบบหนึ่งว่าเป็น ภาษาที่ M ยอมรับโดยสถานะยอมรับ (accept by accepting state)
• จากนิยามของการยอมรับโดยกองซ้อนว่าง เราพบว่าสถานะสุดท้ายของเครื่องออโตมาตากดลงไม่มีความสำคัญ เราอาจไม่ใส่ F ในการนิยามเครื่องออโตมาตากดลงเช่น M = (Q, , , , q₀, Z₀) แทนออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่าง

ตัวอย่างที่ 11 จงสร้างออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่างสำหรับภาษา L = {ww^R | w {0,1}^* }
ตัวอย่างที่ 12 จงสร้างออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่างสำหรับภาษา L = {x {0,1}^* | x = x^R}
ตัวอย่างที่ 13 จงสร้างออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่างสำหรับภาษา L = {w {0,1}^* | n(1, w) = n(0, w)}