ไวยากรณ์ (grammar)
งานอย่างหนึ่งที่เรามักใช้คอมพิวเตอร์ช่วย คือการตรวจวากยสัมพันธ์ (Syntax) ของการเขียนโปรแกรมภาษาซี
เรามักต้องใช้โครงสร้างการซ้อนใน (nested structure) ซึ่งการเขียนในลักษณะนี้จะได้เซตของสัญลักษณ์ที่เป็นไปได้
ไม่ใช่เซตปกติ เพราะถ้าเราพิจารณา L = {anbn | n 
 } และเมื่อเราแทน a ด้วย ( และ b ด้วย ) เราจะเห็นได้ว่า สายอักขระที่ L
ยอมรับต้องมีจำนวนวงเล็บเปิดเท่ากับจำนวนวงเล็บปิดและต้องมีวงเล็บเปิดขึ้นหน้าก่อนเสมอ L เป็นภาษาที่มีลักษณะโครงสร้างการซ้อนใน
แต่ภาษานี้ไม่ใช่ภาษาปกติ ดังนั้นเราไม่สามารถใช้ออโตมาตาจำกัดเชิงกำหนด ช่วยในการตรวจสอบวากยสัมพันธ์
เราจำเป็นต้องใช้เครื่องออโตมาตาที่มีความสามารถมากกว่า ออโตมาตาจำกัดเชิงกำหนด (นั่นคือออโตมาตากดลง)
โดยเราจะสนใจภาษาที่ออโตมาตาประเภทใหม่นี้ยอมรับได้ } และเมื่อเราแทน a ด้วย ( และ b ด้วย ) เราจะเห็นได้ว่า สายอักขระที่ L
ยอมรับต้องมีจำนวนวงเล็บเปิดเท่ากับจำนวนวงเล็บปิดและต้องมีวงเล็บเปิดขึ้นหน้าก่อนเสมอ L เป็นภาษาที่มีลักษณะโครงสร้างการซ้อนใน
แต่ภาษานี้ไม่ใช่ภาษาปกติ ดังนั้นเราไม่สามารถใช้ออโตมาตาจำกัดเชิงกำหนด ช่วยในการตรวจสอบวากยสัมพันธ์
เราจำเป็นต้องใช้เครื่องออโตมาตาที่มีความสามารถมากกว่า ออโตมาตาจำกัดเชิงกำหนด (นั่นคือออโตมาตากดลง)
โดยเราจะสนใจภาษาที่ออโตมาตาประเภทใหม่นี้ยอมรับได้
เราเริ่มด้วยการพิจารณาไวยากรณ์ที่ใช้ในชีวิตประจำวัน พิจารณากฎในการสร้างประโยคในภาษาอังกฤษ
| sentence | สร้างได้จาก
noun phrase ตามด้วย verb |
| noun phrase | อนุญาต
ให้เป็น noun หรือ adjective ตามด้วย noun phrase |
| noun | อาจเป็น
boy หรือ girl |
| adjective | ให้เป็น
little เท่านั้น |
| verb | ให้เป็น
walk เท่านั้น |
ประโยคที่เกิดจากกฎเหล่านี้เช่น little boy walk, little little girl walk เราเขียนกฎข้อ (1)-(5) ได้ดังนี้
| < sentence > |
 |
< noun phrase > < verb > |
| < noun phrase > |
 |
< noun > | < adjective > < noun phrase > |
| < noun > |
 |
boy | girl |
| < adjective > |
 |
little |
| < verb > |
 |
walk |
หรือในรูปแบบ บีเอ็นเอฟ (BNF) คือ
| < sentence > |
:: = |
< noun phrase > < verb > |
| < noun phrase > |
:: = |
< noun > | < adjective > < noun phrase > |
| < noun > |
:: = |
boy | girl |
| < adjective > |
:: = |
little |
| < verb > |
:: = |
walk |
กฎทั้งหมดที่เขียนขึ้นรวมกันเรียกว่าไวยากรณ์ (Grammar) เราเรียก walk, little, boy และ girl ว่าเป็น คำปลายทาง (terminal) เนื่องจากคำเหล่านี้
ไม่มีการเขียนขยายความหมายต่อไปได้ ส่วน < noun >, < noun phrase >, < adjective >, < verb >, < sentence
> ซึ่งเราใช้กฎในการเปลี่ยนได้เรื่อยๆ (เช่น little boy, little girl, little little boy, little little girl เป็น noun phrase ทั้งสิ้น) จึงเรียกคำเหล่านี้ว่า
การผลิต (production) และเรียก < sentence > ว่า สัญลักษณ์เริ่มต้น (start symbol)
ข้อสังเกตุ ส่วนของไวยากรณ์ที่เราเขียนข้างต้นจะไม่มีคำปลายทางปรากฎอยู่ทางซ้ายของกฎ
ทำให้เราเรียกไวยากรณ์ประเภทนี้ว่า ไวยากรณ์ไม่พึ่งบริบท
บทนิยาม ไวยากรณ์ไม่พึ่งบริบท (context-free grammar) แต่ละชุดประกอบด้วย
- เซตของตัวแปร (variables) ทั้งหมดซึ่งเป็นเซตจำกัด V
- เซตของคำปลายทาง (terminals) ทั้งหมดซึ่งเป็นเซตจำกัด T
- เซตของกฎการผลิต (production rules) ทั้งหมดซึ่งเป็นเซตจำกัด P
และมีเงื่อนไขที่ว่าแต่ละการผลิต (production) ใน P ต้องอยู่ในรูปแบบ A

 เมื่อ A เมื่อ A  V และ V และ
  (V (V
 T)* T)*
- สัญลักษณ์เริ่มต้น (Start ymbol) S ซึ่งต้องเป็นสมาชิกของ V
เขียนแทนไวยากรณ์ไม่พึ่งบริบทแต่ละชุดด้วย <V, T, P, S >
หมายเหตุ สัญลักษณ์ A 
 1 | 1 |  2 | . . . | 2 | . . . |
 n
หมายถึง A n
หมายถึง A   1 หรือ
A 1 หรือ
A   2 หรือ . . . หรือ
A 2 หรือ . . . หรือ
A   n n
ตัวอย่างที่ 1:
<{S}, {a, b}, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทชุดหนึ่งเมื่อ P ประกอบด้วย S  aSb | ab
aSb | ab
นิยาม ให้ G = < V, T, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทที่
 , , 
 (V (V  T)* T)*
- เรากล่าวว่า
 แปลงมาจาก แปลงมาจาก  โดยตรง เขียนแทนด้วย
โดยตรง เขียนแทนด้วย  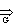
 ก็ต่อเมื่อมี A ก็ต่อเมื่อมี A  V และ V และ
 1, 1,  2, 2,
  (V (V
 T)* ที่ทำให้ T)* ที่ทำให้  = =
 1 A 1 A  2, 2,
 = =  1 1
  2
และ A 2
และ A   เป็นการผลิตใน P เป็นการผลิตใน P
- และ
 แปลงมาจาก แปลงมาจาก  เขียนแทนด้วย
เขียนแทนด้วย  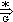
 ก็ต่อเมื่อ ก็ต่อเมื่อ  = =
 หรือมี หรือมี  1, 1,
 2, ..., 2, ...,  n n
 (V (V  T)* ที่ T)* ที่
 1 = 1 =  , ,
 n = n =  และ และ
 1 1 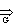
 2, 2,  2 2
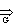  3, ..., 3, ...,
 n-1 n-1 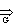
 n
หรือเขียนได้เป็น n
หรือเขียนได้เป็น  1 1 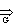
 2 2 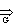 ... ...
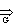  n
และเรียกว่าเป็น การแปลง (derivation) ของ n
และเรียกว่าเป็น การแปลง (derivation) ของ  จาก จาก

ภาษาที่เกิดจาก G เขียนแทนด้วย L(G) คือเซตของสายอักขระ w  T*
โดยที่ w แปลงมาจาก S ดังนั้น L(G) = {w T*
โดยที่ w แปลงมาจาก S ดังนั้น L(G) = {w  T* | S T* | S
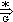 w} และเรียกสมาชิกทุกตัวใน L(G) ว่า ประโยค w} และเรียกสมาชิกทุกตัวใน L(G) ว่า ประโยค
ภาษา L จะเป็น ภาษาไม่พึ่งบริบท (Context-free language) ซึ่งเรียกสั้นๆ ว่า ซีเอฟแอล (CFL) ก็ต่อเมื่อ เราสามารถหา
ไวยากรณ์ไม่พึ่งบริบท G ซึ่ง L = L(G) เรากล่าวว่า G ก่อกำเนิด L
- G1 สมมูลกับ G2 ก็ต่อเมื่อ L(G1) = L(G2)
จาก ตัวอย่างที่ 1 ให้ G = <{S}, {a, b}, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทที่มี P เป็นเซตของการผลิตที่ประกอบด้วย
S  aSb | ab aSb | ab
จงตรวจสอบว่า S 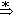 aaabbb และ
S aaabbb และ
S 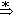 aababbb หรือไม่ และจงหา L(G) aababbb หรือไม่ และจงหา L(G)
การแสดงว่า S 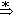 aaabbb เราอาจใช้แผนภาพที่เรียกว่า ต้นไม้การแปลงเพื่อแสดงการใช้กฎดังนิยาม aaabbb เราอาจใช้แผนภาพที่เรียกว่า ต้นไม้การแปลงเพื่อแสดงการใช้กฎดังนิยาม
นิยาม ให้ G = <V, T, P, S > เป็นไวยากรณ์ไม่พึ่งบริบท เรากำหนดให้ ต้นไม้การแปลง
(derivation tree) คือกราฟที่มีทิศทาง (directed graph) ที่เป็นต้นไม้ซึ่งสอดคล้องเงื่อนไขต่อไปนี้
- จุดยอดแต่ละจุดเป็นสมาชิกของ V
 T T
 { { } }
- รากคือ S
- ใบไม้ทุกใบเป็นสมาชิกของ T
 {
{ } }
- จุดยอดทุกจุดที่ไม่ใช่ใบไม้เป็นสมาชิกของ V
- จุดยอดใดก็ตามที่มี A
 V เขียนกำกับ ถ้าลูกของ A (จากซ้ายไปขวา) คือ
x1, x2, ..., xn แล้ว A V เขียนกำกับ ถ้าลูกของ A (จากซ้ายไปขวา) คือ
x1, x2, ..., xn แล้ว A  x1
x2 ... xn เป็นการผลิตแบบหนึ่งใน P โดยที่ลำดับการปรากฎของลูกจากซ้ายไปขวามีความสำคัญ x1
x2 ... xn เป็นการผลิตแบบหนึ่งใน P โดยที่ลำดับการปรากฎของลูกจากซ้ายไปขวามีความสำคัญ
- จุดยอดที่มี
 เขียนกำกับต้องไม่มีพี่และน้อง (sibling) เขียนกำกับต้องไม่มีพี่และน้อง (sibling)
สำหรับต้นไม้การแปลง เราอาจไม่สนใจต้นไม้ที่มีรากเป็น S เสมอ และใบไม้ก็อาจไม่จำเป็นต้องเป็นคำปลายทางหรือ
 ซึ่งเราเรียกต้นไม้ประเภทนี้ว่า ต้นไม้การแปลงย่อย (Partial derivation tree)
เป็นกราฟที่มีทิศทางที่เป็นต้นไม้ซึ่งสอดคล้องกับเงื่อนไขของต้นไม้การแปลง (1), (4), (5) และ (6) ซึ่งเราเรียกต้นไม้ประเภทนี้ว่า ต้นไม้การแปลงย่อย (Partial derivation tree)
เป็นกราฟที่มีทิศทางที่เป็นต้นไม้ซึ่งสอดคล้องกับเงื่อนไขของต้นไม้การแปลง (1), (4), (5) และ (6)
เรานิยามว่า ต้นไม้การแปลงหรือต้นไม้การแปลงย่อย ผลิต (yield) สายอักขระ 
 (V (V  T)* ก็ต่อเมื่อ T)* ก็ต่อเมื่อ
 เป็นสายอักขระที่ได้จากการอ่านสัญลักษณ์ที่เขียนกำกับใบไม้ทุกใบจากซ้ายไปขวา
ในกรณีที่พบ เป็นสายอักขระที่ได้จากการอ่านสัญลักษณ์ที่เขียนกำกับใบไม้ทุกใบจากซ้ายไปขวา
ในกรณีที่พบ  เราลดรูปโดยไม่เขียนสัญลักษณ์ เราลดรูปโดยไม่เขียนสัญลักษณ์

ตัวอย่างที่ 2: ให้ G = <{S, A, B}, {a, b}, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทที่มี
- S
 aAB, A aAB, A  bBb,
B bBb,
B  A | A | 
จงเขียนต้นไม้การแปลงที่ผลิตสายอักขระ abbbb และจงเขียนต้นไม้การแปลงย่อยที่ผลิตสายอักขระ abBbB
เราพบว่ามีการแปลงอย่างน้อยสองแบบที่เกิดจากต้นไม้การแปลงนี้คือ
- S
 aAB aAB  abBbB abBbB
 abbB abbB  abbA abbA
 abbbBb abbbBb  abbbb abbbb
- S
 aAB aAB  aAA aAA
 aAbBb aAbBb  aAbb aAbb
 abBbbb abBbbb  abbbb abbbb
เราเรียกการแปลงแบบแรกว่า การแปลงซ้ายสุด (leftmost derivation) ซึ่งหมายความว่าตัวแปรถูกแทนที่โดยเริ่มจากตัวแปรที่อยู่ทางซ้ายสุดของสายอักขระ
การแปลงไล่ไปทางขวาจนได้สายอักขระที่ต้องการ และเราเรียกการแปลงแบบที่สองว่า การแปลงขวาสุด (rightmost derivation)
ซึ่งหมายความว่าตัวแปรที่อยู่ทางขวาสุดถูกแทนที่ไล่มาทางขวามาซ้ายจนไม่มีตัวแปรเหลืออยู่เลย
นิยาม ให้ G = < V, T, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทชุดหนึ่งและ
 1 1 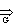
 2 2 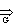 ... ...
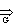  n
เป็นการแปลงของ n
เป็นการแปลงของ  n จาก n จาก
 1 1
จะกล่าวว่า การแปลงนี้เป็น การแปลงซ้ายสุด (Leftmost derivation) ก็ต่อเมื่อ ทุก k  {1, 2, ...,
n-1} เราใช้การผลิตกับตัวแปรซ้ายสุดใน {1, 2, ...,
n-1} เราใช้การผลิตกับตัวแปรซ้ายสุดใน  k เสมอ
ในทำนองเดียวกัน การแปลงนี้เป็น การแปลงขวาสุด (Rightmost derivation) ก็ต่อเมื่อ ทุก k k เสมอ
ในทำนองเดียวกัน การแปลงนี้เป็น การแปลงขวาสุด (Rightmost derivation) ก็ต่อเมื่อ ทุก k  {1, 2, ..., n-1} เราใช้การผลิตกับตัวแปรขวาสุดใน
{1, 2, ..., n-1} เราใช้การผลิตกับตัวแปรขวาสุดใน  k เสมอ k เสมอ
สำหรับไวยากรณ์ไม่พึ่งบริบทใดๆ ที่ G = < V, T, P, S >
ทุก w ที่แปลงมาจาก S จะมีต้นไม้การแปลงในไวยากรณ์ไม่พึ่งบริบทเสมอที่สมนัยกับการแปลงนั้น
ไวยากรณ์ไม่พึ่งบริบทบางไวยากรณ์อาจก่อกำเนิดสายอักขระ w ที่มีต้นไม้การแปลงที่ผลิต w ได้มากกว่าหนึ่งต้น
เราเรียกไวยากรณ์ไม่พึ่งบริบทนี้ว่า กำกวม
ตัวอย่างที่ 3: ให้ G = < V, T, P, E > เป็นไวยากรณ์ไม่พึ่งบริบทที่มี V = {E, I}, T = {a, b, c, +, *, (, ) }
และ P เป็นเซตของการผลิต
- E
 I | E + E | E * E | (E), I I | E + E | E * E | (E), I  a | b | c
a | b | c
สายอักขระในภาษาที่ได้จะมีลักษณะคล้ายกับนิพจน์การคำนวณในภาษา FORTRAN หรือ PASCAL และถ้าเราพิจารณาสายอักขระ a + b * c เราจะได้ต้นไม้การผลิตสองต้นคือ
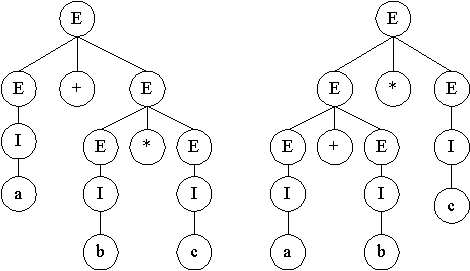
นิยาม ให้ G = < V, T, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทชุดหนึ่ง เรากล่าวว่า G กำกวม
(ambiguous) ก็ต่อเมื่อ มี w  L(G) ที่มีต้นไม้การแปลงที่ผลิต w มากกว่า 1 ต้น L(G) ที่มีต้นไม้การแปลงที่ผลิต w มากกว่า 1 ต้น
- สำหรับภาษาไม่พึ่งบริบท L ใด ๆ L เป็น ภาษาที่ไม่กำกวม (unambiguous) ก็ต่อเมื่อ มีไวยากรณ์ไม่พึ่งบริบทที่ไม่กำกวมก่อกำเนิด L
- เรากล่าวว่า L กำกวมแบบฝังติด (inherently ambiguous) ก็ต่อเมื่อสำหรับไวยากรณ์ไม่พึ่งบริบททุกไวยากรณ์ G ที่ก่อกำเนิด L,
ไวยากรณ์ G นั้นกำกวมเสมอ
ตัวอย่างที่ 2 เป็นตัวอย่างของไวยากรณ์ไม่พึ่งบริบท G ที่กำกวม (ambiguous) แต่ L(G) เป็นภาษาไม่พึ่งบริบทที่ไม่กำกวม (unambiguous)
เพราะเราสามารถสร้างไวยากรณ์ไม่พึ่งบริบทที่ไม่กำกวมที่สมมูลกับ L(G) ได้คือ
G' = < {E, A, B, I}, {a, b, c, +, *, (, ) }, P, E > โดยที่เซตของการผลิต P ประกอบไปด้วย
- E
 E+A | A, A E+A | A, A  B | A*B,
B B | A*B,
B  I | (E), I I | (E), I  a | b | c a | b | c
ตัวอย่างที่ 4: ให้ L1 = {anbncmdm |
m, n   }, L2 =
{anbmcmdn | m, n }, L2 =
{anbmcmdn | m, n 
 }, และ L = L1 }, และ L = L1  L2
จะได้ว่า L1, L2 และ L เป็นภาษาไม่พึ่งบริบท เพราะเราสามารถหาไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิดภาษาเหล่านี้ได้คือ L2
จะได้ว่า L1, L2 และ L เป็นภาษาไม่พึ่งบริบท เพราะเราสามารถหาไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิดภาษาเหล่านี้ได้คือ
- G1 = < {S1, A, B}, {a, b, c, d }, P1, S1 > โดยที่เซตของการผลิต
P1 ประกอบไปด้วย S1
 aAbcBd, A aAbcBd, A
 aAb | aAb |  , B , B
 cBd | cBd | 
- G2 = < {S2, C, D}, {a, b, c, d }, P2, S2 > โดยที่เซตของการผลิต
P2 ประกอบไปด้วย S2
 aCd, C aCd, C
 aDd | bDc | bc, D aDd | bDc | bc, D  bDc | bc bDc | bc
- G = < {S, S1, S2, A, B, C, D}, {a, b, c, d }, P, S > โดยที่เซตของการผลิต
P ประกอบไปด้วย S
 S1 | S2, S1 S1 | S2, S1
 aAbcBd, A aAbcBd, A  aAb | aAb |
 , B , B  cBd | cBd |
 , S2 , S2  aCd, C aCd, C
 aDd | bDc | bc, D aDd | bDc | bc, D  bDc | bc bDc | bc
ประโยคในรูป anbncndn เป็นสมาชิกตัวหนึ่งใน L =
L1  L2 ซึ่งเราสามารถสร้างการผลิตโดยใช้กฎที่เกี่ยวข้องกับ
S1, A, B หรือ กฎที่เกี่ยวข้องกับ S2, C, D ทำให้ได้ต้นไม้การแปลงสองต้นเป็นอย่างน้อยดังนั้น ไวยากรณ์ G กำกวม L2 ซึ่งเราสามารถสร้างการผลิตโดยใช้กฎที่เกี่ยวข้องกับ
S1, A, B หรือ กฎที่เกี่ยวข้องกับ S2, C, D ทำให้ได้ต้นไม้การแปลงสองต้นเป็นอย่างน้อยดังนั้น ไวยากรณ์ G กำกวม
สำหรับตัวอย่างนี้ เราไม่สามารถหาไวยากรณ์ไม่พึ่งบริบทที่ไม่กำกวมได้ ด้วยเหตุผลดังนี้
- ถ้าเราสมมติว่ามีไวยากรณ์ไม่พึ่งบริบทที่ไม่กำกวมก่อกำเนิดภาษานี้ เราต้องได้ว่าไวยากรณ์ที่ไม่กำกวมนั้นต้องสามารถสร้างประโยคในรูปแบบ
anbncndn ได้เสมอ และต้องมีต้นไม้การแปลงทางซ้ายเพียงแบบเดียว เราเพียงปรับต้นไม้การแปลง
ที่ได้จากกฎที่เกี่ยวข้องกับ S1, A, B เป็นกฎของ S2 ที่ใช้ C, D เราจะยังคงได้ประโยคเดิมแต่มีต้นไม้การแปลงสองต้นที่ต่างกัน
เกิดการขัดแย้ง
ทำให้ได้ว่าภาษาไม่พึ่งบริบทนี้เป็นภาษากำกวมแบบฝังติด
นอกจากไวยากรณ์ที่กำกวมแล้ว เราอาจมีไวยากรณ์ไม่พึ่งบริบทที่มีกฎการผลิตบางกฎที่ไม่มีโอกาสถูกใช้สร้างประโยค เนื่องจากตัวแปร
ไม่มีการแปลงที่เกิดมาจาก S ได้ ตัวอย่างเช่น
G = < {S,A,B}, {a}, P, S > โดยที่เซตของการผลิต P ประกอบด้วย S  AB | aAS | a, A
AB | aAS | a, A  a ซึ่งไม่มีประโยคที่เกิดจากตัวแปร B เราจะเรียกตัวแปร B นี้ว่า
ตัวแปรไร้ประโยชน์ (useless variable) และเรียกการผลิต S a ซึ่งไม่มีประโยคที่เกิดจากตัวแปร B เราจะเรียกตัวแปร B นี้ว่า
ตัวแปรไร้ประโยชน์ (useless variable) และเรียกการผลิต S  AB ว่า
การผลิตไร้ประโยชน์ (useless production) ซึ่งในกรณีนี้ เราสามารถสร้างไวยากรณ์ไม่พึ่งบริบทที่สมมูลกับ G โดยไม่มีตัวแปรไร้ประโยชน์ได้คือ AB ว่า
การผลิตไร้ประโยชน์ (useless production) ซึ่งในกรณีนี้ เราสามารถสร้างไวยากรณ์ไม่พึ่งบริบทที่สมมูลกับ G โดยไม่มีตัวแปรไร้ประโยชน์ได้คือ
G' = < {S,A}, {a}, P', S > โดยที่ P' ประกอบด้วย S  aAS | a, A aAS | a, A
 a จะได้ L(G) = L(G') a จะได้ L(G) = L(G')
นิยาม
ให้ G = < V, T, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทชุดหนึ่งและ A  V, V,
- A เป็น ตัวแปรมีประโยชน์ (useful variable) ก็ต่อเมื่อ มี w
 L(G) และ
x, y L(G) และ
x, y  (V (V  T)*
ที่ทำให้ S T)*
ที่ทำให้ S 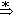 xAy xAy 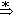 w w
- สำหรับตัวแปรตัวใดที่ไม่ใช่ตัวแปรมีประโยชน์ เราจะเรียกตัวแปรนั้นว่า ตัวแปรไร้ประโยชน์ (useless variable) และ
การผลิตที่มีตัวแปรไร้ประโยชน์อยู่ จะเรียกว่า การผลิตไร้ประโยชน์ (useless production)
ในการบ่งบอกว่าตัวแปรใดเป็นตัวแปรไร้ประโยชน์ เราสามารถใช้กราฟพึ่งพาได้ซึ่งนิยามดังนี้
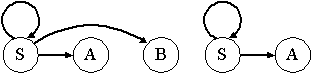
นิยาม กราฟพึ่งพา (Dependency graph) คือกราฟเทียมที่มีทิศทาง โดยที่เซตของจุดยอดคือ
เซตของตัวแปรทั้งหมด และเซตของอาร์ก นิยามโดย
- สำหรับตัวแปร A และ B ใดๆ จะมีอาร์กจากจุดยอด A ไปจุดยอด B ก็ต่อเมื่อมี x, y
 (V (V  T)* ที่ทำให้
A T)* ที่ทำให้
A  xBy เป็นการผลิตแบบหนึ่ง xBy เป็นการผลิตแบบหนึ่ง
ตัวอย่างของกราฟพึ่งพา เช่น
ทฤษฎีบท สำหรับแต่ละไวยากรณ์ไม่พึ่งบริบท G = < V, T, P, S > ถ้า L(G)
 Ø แล้วจะมีไวยากรณ์ไม่พึ่งบริบท G' = < V', T', P', S > ที่ L(G') = L(G) โดยที่ G'
ไม่มีทั้งตัวแปรไร้ประโยชน์ และการผลิตไร้ประโยชน์ Ø แล้วจะมีไวยากรณ์ไม่พึ่งบริบท G' = < V', T', P', S > ที่ L(G') = L(G) โดยที่ G'
ไม่มีทั้งตัวแปรไร้ประโยชน์ และการผลิตไร้ประโยชน์
พิสูจน์ ส่วนที่ 1: สร้าง G' = < V', T, P', S > โดยที่ V' = {A  V | มี w V | มี w
 T* ที่ A T* ที่ A 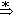 w } ดังนี้ w } ดังนี้
- (1.1) ให้ V1 = {A
 V | มี w V | มี w
 T* ที่ A T* ที่ A  w เป็นการผลิตใน P } w เป็นการผลิตใน P }
- (1.2) สำหรับแต่ละ n
  ให้
Vn+1 = Vn ให้
Vn+1 = Vn  { B { B  V
| มี V
| มี   (Vn (Vn
 T)* ที่ B T)* ที่ B 
 เป็นการผลิตใน P } เป็นการผลิตใน P }
- ทำซ้ำ (1.2) จนกระทั่งได้ L
  ที่
VL+1 = VL เรียกเซตนั้นว่า V' นั่นคือ V' = VL ที่
VL+1 = VL เรียกเซตนั้นว่า V' นั่นคือ V' = VL
- (1.3) ให้ P' เป็นเซตของการผลิตทั้งหมดใน P ที่สัญลักษณ์ทั้งหมดที่ปรากฎในการผลิต เหล่านั้นเป็นสมาชิกของ
(V'
 T) T)
ตัวอย่างที่ 5: กำหนดให้ G = < {S, A, B, C}, {a,b}, P, S > เป็นไวยากรณ์ไม่พึ่งบริบท โดยที่เซตของการผลิต
P ประกอบด้วย S  aS | A | C, A aS | A | C, A  a,
B a,
B  aa, C aa, C  aCb aCb
- ใช้ (1.1) ได้ V1 = { A, B }
- ใช้ (1.2) ได้ V2 = { A, B }
 {S} ใช้ (1.2) อีกครั้งเราพบว่า V3 = V2 {S} ใช้ (1.2) อีกครั้งเราพบว่า V3 = V2
- ดังนั้น V' = {S, A, B} และ P' ประกอบด้วย S
 aS | A, A aS | A, A
 a, B a, B  aa aa
- เพราะฉะนั้น G' = < {S, A, B}, {a,b}, P', S > เขียนกราฟพึ่งพาดังนี้
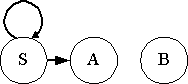
พิสูจน์ ส่วนที่ 2:
สร้าง Gh จาก G' โดยเริ่มจากการเขียนกราฟพึ่งพาของ G' และให้ Vh เป็นเซตของตัวแปร
ทั้งหมดใน V' ที่มี path จาก S และ Ph เป็นเซตของการผลิตทั้งหมดใน P' ที่สัญลักษณ์ทั้งหมดที่ปรากฎในการผลิตเหล่านั้น
เป็นสมาชิกของ (Vh  T) ให้ Th = T
จากตัวอย่างจึงได้ Vh = {S, A}, Ph = { S T) ให้ Th = T
จากตัวอย่างจึงได้ Vh = {S, A}, Ph = { S  aS,
S aS,
S  A, A A, A  a} และ Gh =
< {S, A}, {a, b}, Ph, S > ตามต้องการ a} และ Gh =
< {S, A}, {a, b}, Ph, S > ตามต้องการ
นิยาม การผลิต- (
( -production) คือการผลิตในไวยากรณ์ไม่พึ่งบริบทที่อยู่ในรูปแบบ A -production) คือการผลิตในไวยากรณ์ไม่พึ่งบริบทที่อยู่ในรูปแบบ A
  และ เราเรียกตัวแปร A นี้ว่า
ตัวแปรว่าง (nullable) ซึ่งหมายถึงตัวแปรที่ผลิต และ เราเรียกตัวแปร A นี้ว่า
ตัวแปรว่าง (nullable) ซึ่งหมายถึงตัวแปรที่ผลิต 
ตัวอย่างที่ 6: กำหนดไวยากรณ์ไม่พึ่งบริบท G = < {S, A, B, C, D}, {a, b, d}, P, S > ซึ่งมีเซตของการผลิต
P คือ S  ABaC, A ABaC, A  BC, B BC, B
 b | b |  , C , C
 D | D |  , D , D
 d d
จงหาไวยากรณ์ไม่พึ่งบริบทที่สมมูลกับ G โดยที่ไวยากรณ์ใหม่นี้ไม่มีการผลิต-
ขั้นที่ 1 หาเซตของตัวแปรว่างทั้งหมด V'
- (1.1) เริ่มต้นใส่ตัวแปรทุกตัวที่ให้การผลิต-
 เข้าไปใน V1 เข้าไปใน V1
- (1.2) ใส่ตัวแปรทุกตัวใน Vn เข้าใน Vn+1 และใส่ตัวแปร X ใด ๆ ที่ X
 X1 X2 . . . Xn เป็นการผลิตใน P โดย
X1, X2, . . ., Xn ปรากฏใน Vn เข้าไปใน Vn+1 X1 X2 . . . Xn เป็นการผลิตใน P โดย
X1, X2, . . ., Xn ปรากฏใน Vn เข้าไปใน Vn+1
- (1.3) ทำ (1.2) ไปเรื่อยๆ จนกระทั่ง Vk+1 = Vk เราเรียกเซตของตัวแปรว่างใหม่นี้ว่า V'
เมื่อเราใช้ขั้นตอนวิธีนี้กับตัวอย่างที่หนึ่ง จาก (1.1) เราได้ V1 = {B, C}, V2 = {B, C, A}, V3 = {B, C, A}
ดังนั้น V' = {A, B, C}
ขั้นที่ 2 สร้างเซตของการผลิต P'
- (2.1) ใส่การผลิตทุกแบบที่ไม่ใช่การผลิต-
 เข้าไปใน P' เข้าไปใน P'
- (2.2) สำหรับการผลิต E
  เมื่อ เมื่อ
  (V' (V'
 T)+ และ T)+ และ  มีตัวแปรว่างปรากฎ
ให้แทนตัวแปรว่างด้วย มีตัวแปรว่างปรากฎ
ให้แทนตัวแปรว่างด้วย  ใส่การผลิตทั้งหมดที่ไม่ใช่
การผลิต- ใส่การผลิตทั้งหมดที่ไม่ใช่
การผลิต- ลงไปใน P' ลงไปใน P'
ใช้ (2.1) ได้ P' = { S  ABaC, A ABaC, A  BC,
B BC,
B  b, C b, C  D,
D D,
D  d} d}
(2.2) กับ C ได้ P' = P'  { A { A  B,
S B,
S  ABa} ABa}
(2.2) กับ B ได้ P' = P'  { A { A  C,
S C,
S  AaC, S AaC, S  Aa} Aa}
(2.2) กับ A ได้ P' = P'  {S {S  BaC |
Ba, ac, Aa, a} BaC |
Ba, ac, Aa, a}
จะได้การผลิตใหม่คือ
- S
 ABaC | BaC | AaC | ABa | aC | Aa | Ba | a, ABaC | BaC | AaC | ABa | aC | Aa | Ba | a,
- A
 B | C | BC, B | C | BC,
- B
 b, C b, C  D,
D D,
D  d d
ขั้นที่ 3 ให้ G' = < V', T, P', S > ตามที่สร้างข้างต้น เราจะได้ว่า L(G') = L(G)
ทฤษฎีบท สำหรับไวยากรณ์ไม่พึ่งบริบท G ใด ๆ ถ้า 
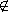 L(G) แล้วจะมีไวยากรณ์ไม่พึ่งบริบท G' ที่สมมูลกับ G และ G'
ไม่มีการผลิต- L(G) แล้วจะมีไวยากรณ์ไม่พึ่งบริบท G' ที่สมมูลกับ G และ G'
ไม่มีการผลิต-
บทแทรก ถ้า L เป็นภาษาไม่พึ่งบริบทโดยที่ 
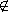 L และ L L และ L Ø แล้วจะมีไวยากรณ์ไม่พึ่งบริบท
G' ที่ L = L(G') และ G' ไม่มีตัวแปรไร้ประโยชน์ การผลิตไร้ประโยชน์ และการผลิต- Ø แล้วจะมีไวยากรณ์ไม่พึ่งบริบท
G' ที่ L = L(G') และ G' ไม่มีตัวแปรไร้ประโยชน์ การผลิตไร้ประโยชน์ และการผลิต-
ในบางกรณีไวยากรณ์ไม่พึ่งบริบท อาจมีกฎการผลิตที่อยู่ในรูปแบบ A  B โดยที่ A และ B
ต่างก็เป็นตัวแปร เราสามารถลดกฎการผลิตนี้ได้ B โดยที่ A และ B
ต่างก็เป็นตัวแปร เราสามารถลดกฎการผลิตนี้ได้
นิยาม สำหรับไวยากรณ์ไม่พึ่งบริบท เราจะเรียกการผลิตที่อยู่ในรูปแบบ A
 B โดยที่ A และ B เป็นตัวแปรว่า การผลิตหนึ่งหน่วย (unit production) B โดยที่ A และ B เป็นตัวแปรว่า การผลิตหนึ่งหน่วย (unit production)
ตัวอย่างที่ 7: ให้ G = < {S,A,B}, {a,b,c}, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทที่มีเซตของการผลิต P ดังนี้
S  Aa | B, B Aa | B, B  A | bb,
A A | bb,
A  a | bc | B a | bc | B
จงหาไวยากรณ์ไม่พึ่งบริบท G' ที่สมมูลกับ G โดยที่ G' ไม่มีการผลิตหนึ่งหน่วย
ขั้นที่ 1 เขียนกราฟของการผลิตหนึ่งหน่วยทุกแบบ
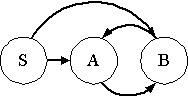
S  B, B B, B  A,
A A,
A  B จะได้ S B จะได้ S 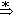 A A
ขั้นที่ 2 สร้างเซตของการผลิต P'
(2.1) ใส่การผลิตทุกแบบที่ไม่ใช่การผลิตหนึ่งหน่วยเข้าไปใน P'
(2.2) สำหรับการผลิต X  Y ถ้า Y Y ถ้า Y 
 เป็นการผลิตที่อยู่ใน P' ให้ใส่การผลิต X เป็นการผลิตที่อยู่ใน P' ให้ใส่การผลิต X 
 ใน P' ใน P'
จากตัวอย่าง เราจะเพิ่มการผลิตต่อไปนี้ใน P'
- A
 bb เพราะ A bb เพราะ A 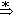 B
และ B B
และ B  bb bb
- B
 a | bc เพราะ B a | bc เพราะ B 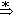 A และ
A A และ
A  a | bc a | bc
- S
 bb | a | bc เพราะ S bb | a | bc เพราะ S 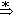 B และ
B B และ
B  bb | a | bc bb | a | bc
- S
 a | bc | bb เพราะ S a | bc | bb เพราะ S 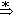 A และ
A A และ
A  a | bc | bb แต่เนื่องจากเราได้เพิ่มการผลิตเหล่านี้แล้ว เราไม่จำเป็นต้องมีการผลิตนี้อีก a | bc | bb แต่เนื่องจากเราได้เพิ่มการผลิตเหล่านี้แล้ว เราไม่จำเป็นต้องมีการผลิตนี้อีก
จะได้ว่า G' = < {S, A, B}, {a, b, c}, P', S > ไม่มีการผลิตหนึ่งหน่วย และ L(G') = L(G)
ทฤษฎีบท สำหรับไวยากรณ์ไม่พึ่งบริบท G ถ้า 
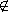 L(G) แล้วจะมีไวยากรณ์ไม่พึ่งบริบท G' ที่สมมูลกับ G และ G' ไม่มีการผลิตหนึ่งหน่วย L(G) แล้วจะมีไวยากรณ์ไม่พึ่งบริบท G' ที่สมมูลกับ G และ G' ไม่มีการผลิตหนึ่งหน่วย
บทแทรก ถ้า L เป็นภาษาไม่พึ่งบริบทโดยที่ 
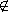 L และ L L และ L  Ø
แล้วจะมีไวยากรณ์ไม่พึ่งบริบท G' ที่ L = L(G') และ G' ไม่มีตัวแปรไร้ประโยชน์ ไม่มีการผลิตไร้ประโยชน์
ไม่มีการผลิต- Ø
แล้วจะมีไวยากรณ์ไม่พึ่งบริบท G' ที่ L = L(G') และ G' ไม่มีตัวแปรไร้ประโยชน์ ไม่มีการผลิตไร้ประโยชน์
ไม่มีการผลิต- และไม่มีการผลิตหนึ่งหน่วย และไม่มีการผลิตหนึ่งหน่วย
อย่างไรก็ตาม ภาษาไม่พึ่งบริบทอาจมี  อยู่ในภาษา
เราสามารถหาไวยากรณ์ไม่พึ่งบริบทที่ไม่มีการผลิตหนึ่งหน่วย ไม่มีการผลิต- อยู่ในภาษา
เราสามารถหาไวยากรณ์ไม่พึ่งบริบทที่ไม่มีการผลิตหนึ่งหน่วย ไม่มีการผลิต- ก่อน
แล้วจึงเติมกลับเข้าในภาษา โดยใช้ทฤษฎีบทต่อไปนี้ ก่อน
แล้วจึงเติมกลับเข้าในภาษา โดยใช้ทฤษฎีบทต่อไปนี้
ทฤษฎีบท สำหรับภาษาไม่พึ่งบริบท L ซึ่งมี 
 L เราจะพิจารณาการหาไวยากรณ์ไม่พึ่งบริบท G สำหรับ L -
{ L เราจะพิจารณาการหาไวยากรณ์ไม่พึ่งบริบท G สำหรับ L -
{ } = L(G) เมื่อ G = < V, T, P, S > โดยเราสามารถสร้างไวยากรณ์ไม่พึ่งบริบทที่ยอมรับ L
จาก G ได้ดังนี้ G' = < V', T, P', S' > โดยที่ V' = V } = L(G) เมื่อ G = < V, T, P, S > โดยเราสามารถสร้างไวยากรณ์ไม่พึ่งบริบทที่ยอมรับ L
จาก G ได้ดังนี้ G' = < V', T, P', S' > โดยที่ V' = V  {S'}
และ P' = P {S'}
และ P' = P  {S' {S'  S,
S' S,
S'   } }
|
|