รูปแบบบรรทัดฐาน (Normal form)
จากตัวอย่างของการเขียนไวยากรณ์ไม่พึ่งบริบทที่ผ่านมา เราพบว่าการผลิตมีนิยามที่อิสระในการเขียนทำให้การตรวจสอบ
และเปรียบเทียบภาษาเป็นไปด้วยความยุ่งยาก เพื่อให้เกิดการเขียนรูปแบบไวยากรณ์ตรวจสอบได้ง่าย เราจึงเสนอนิยามรูปแบบบรรทัดฐานเพื่อเพิ่มข้อกำหนดในการเขียนไวยากรณ์
สำหรับรูปแบบบรรทัดฐาน (normal form) ของการผลิตที่เราสนใจมีอยู่ 2 รูปแบบด้วยกันคือ รูปแบบบรรทัดฐานชอมสกี (Chomsky normal form)
และรูปแบบบรรทัดฐานกรายบาค (Greibach normal form) โดยที่เราประกันว่า
ภาษาไม่พึ่งบริบททุกภาษาสามารถเขียนการผลิตให้อยู่ในรูปแบบบรรทัดฐานชอมสกี และอยู่ในรูปแบบบรรทัดฐานกรายบาคได้เสมอ
บทนิยาม การผลิตที่อยู่ในรูป A  BC และ A BC และ A
 a เมื่อ A, B, C เป็นตัวแปรและ a เป็นคำปลายทางจะถูกเรียกว่า
รูปแบบบรรทัดฐานชอมสกี(Chomsky normal form) หรือ ซีเอ็นเอฟ (CNF) และเรียกรูปแบบการผลิต A a เมื่อ A, B, C เป็นตัวแปรและ a เป็นคำปลายทางจะถูกเรียกว่า
รูปแบบบรรทัดฐานชอมสกี(Chomsky normal form) หรือ ซีเอ็นเอฟ (CNF) และเรียกรูปแบบการผลิต A
 a a  เมื่อ
a เป็นคำปลายทาง และ เมื่อ
a เป็นคำปลายทาง และ  เป็นสายอักขระของตัวแปรล้วน หรือ เป็นสายอักขระของตัวแปรล้วน หรือ
 ว่า รูปแบบบรรทัดฐานกรายบาค (Greibach normal form)
หรือ จีเอ็นเอฟ (GNF) ว่า รูปแบบบรรทัดฐานกรายบาค (Greibach normal form)
หรือ จีเอ็นเอฟ (GNF)
ตัวอย่างที่ 1 ให้ G = < {S, A, B}, {a, b}, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทที่มีการผลิต P ประกอบด้วย
- S
 bA| aB, A bA| aB, A
 bAA | aS | a, B bAA | aS | a, B
 aBbA | bS | b aBbA | bS | b
จงหาไวยากรณ์ไม่พึ่งบริบท G' ที่สมมูลกับ G ที่การผลิตทุกแบบใน G' อยู่ในรูปแบบบรรทัดฐานชอมสกี
วิธีทำ เราจะแสดงขั้นตอนการแปลงไวยากรณ์ทีละขั้น ให้ V = {S, A, B} และ T = {a, b}
ขั้นตอนที่ 1 สร้างเซตของตัวแปรใหม่ V' โดยที่ V  V' และ
พิจารณาการผลิตใน P สร้างเซตการผลิตใหม่ P' ดังนี้ V' และ
พิจารณาการผลิตใน P สร้างเซตการผลิตใหม่ P' ดังนี้
- (1.1) ใส่การผลิตที่อยู่ในรูปแบบที่ต้องการแล้วเก็บไว้ใน P'
นั่นคือเก็บ A  a และ B a และ B
 b เข้าไปใน P' b เข้าไปใน P'
- (1.2) สร้างการผลิตสำหรับคำปลายทางทุกตัวใหม่ (โดยปกติจะสนใจเฉพาะคำปลายทางที่ปรากฎในกฎการผลิต)
เนื่องจากการผลิตใน P ที่มีสายอักขระทางขวามือของเครื่องหมาย  มี a
ปรากฏและบางแบบมี b ปรากฏ เราจึงสร้างตัวแปรใหม่ 2 ตัว คือ Ba และ Bb และใส่การผลิต Ba มี a
ปรากฏและบางแบบมี b ปรากฏ เราจึงสร้างตัวแปรใหม่ 2 ตัว คือ Ba และ Bb และใส่การผลิต Ba
 a, Bb a, Bb  b เข้าไปใน P' พร้อมใส่ตัวแปรใหม่ Ba และ Bb ใน V'
b เข้าไปใน P' พร้อมใส่ตัวแปรใหม่ Ba และ Bb ใน V'
- (1.3) เปลี่ยนการผลิตทั้งหมดที่มีคำปลายทางอยู่ทางขวา ด้วยตัวแปรใหม่ที่สร้างขึ้นใน 1.2
จาก S  bA | aB ใส่การผลิต S bA | aB ใส่การผลิต S
 BbA | BaB เข้าไปใน P' BbA | BaB เข้าไปใน P'
จาก A  bAA | aS ใส่การผลิต A bAA | aS ใส่การผลิต A
 BbAA | BaS ใส่เข้าไปใน P' BbAA | BaS ใส่เข้าไปใน P'
จาก B  aBbA | bS ใส่การผลิต B aBbA | bS ใส่การผลิต B
 BaBBbA | BbS ใส่เข้าไปใน P' BaBBbA | BbS ใส่เข้าไปใน P'
ขั้นตอนที่ 2 สร้างตัวแปรใหม่เพื่อให้กฎการผลิตมีตัวแปรสองตัวทางขวาโดย
- (2.1) เพิ่มตัวแปรเพื่อลดความยาวของสายอักขระทางขวามือของเครื่องหมาย
 ใน P' ที่มีความยาวมากกว่า 2 ให้เหลือความยาว 2 ดังนี้
ใน P' ที่มีความยาวมากกว่า 2 ให้เหลือความยาว 2 ดังนี้
จาก A  BbAA สร้างตัวแปรใหม่ C และใส่การผลิต
C BbAA สร้างตัวแปรใหม่ C และใส่การผลิต
C  AA, A AA, A  BbC แทนเข้าไปใน P" BbC แทนเข้าไปใน P"
จาก B  BaBBbA สร้างตัวแปรใหม่ D1,
D2 และใส่การผลิต D1 BaBBbA สร้างตัวแปรใหม่ D1,
D2 และใส่การผลิต D1  BbA, D2 BbA, D2
 BD1, B BD1, B  BaD2 แทนเข้าไปใน P"
BaD2 แทนเข้าไปใน P"
- (2.2) ใส่การผลิตทุกแบบใน P' ที่อยู่ในรูปแบบบรรทัดฐานชอมสกีเข้าไปใน P"
เนื่องจาก S  BbA | BaB, A BbA | BaB, A
 BaS | a, B BaS | a, B  BbS | b เป็นการผลิตทั้งหมดใน P' ที่อยู่ในแบบบรรทัดฐานชอมสกี ดังนั้นจึงใส่การผลิตทั้งหมดนี้เข้าไปใน P"
BbS | b เป็นการผลิตทั้งหมดใน P' ที่อยู่ในแบบบรรทัดฐานชอมสกี ดังนั้นจึงใส่การผลิตทั้งหมดนี้เข้าไปใน P"
- สำหรับ V" = {S, A, B, Ba, Bb, C, D1, D2} จะได้ว่า G" = < V", T, P", S >
เป็นไวยากรณ์ไม่พึ่งบริบทที่มี P" เป็นเชตของการผลิตที่ประกอบไปด้วย
S  BbA | BaB, A BbA | BaB, A
 BaS | BbC | a, B BaS | BbC | a, B
 BbS | BaD2 | b, C BbS | BaD2 | b, C
 AA, D1 AA, D1  BbA,
D2 BbA,
D2  BD1, Ba BD1, Ba
 a, Bb a, Bb  b b
ซึ่ง G" มีกฏการผลิตทั้งหมดในรูปแบบบรรทัดฐานชอมสกี และสามารถพิสูจน์ได้ว่า L(G) = L(G")
เราสามารถขยายวิธีการนี้ไปสู่กรณีทั่วไปได้โดยง่าย ซึ่งจะขอสรุปเป็นทฤษฎีบทง่าย ๆ ดังนี้
ทฤษฏีบท สำหรับไวยากรณ์ไม่พึ่งบริบท G ทุกชุดที่ไม่มีตัวแปรไร้ประโยชน์ การผลิตไร้ประโยชน์
การผลิต- และการผลิตหนึ่งหน่วย จะมีไวยากรณ์ไม่พึ่งบริบท G" ที่สมมูลกับ G
และมีสมบัติว่าการผลิตทุกแบบใน G" อยู่ในรูปแบบบรรทัดฐานชอมสกี (ซีเอ็นเอฟ) และการผลิตหนึ่งหน่วย จะมีไวยากรณ์ไม่พึ่งบริบท G" ที่สมมูลกับ G
และมีสมบัติว่าการผลิตทุกแบบใน G" อยู่ในรูปแบบบรรทัดฐานชอมสกี (ซีเอ็นเอฟ)
บทแทรก สำหรับภาษาไม่พึ่งบริบท L ทุกภาษาที่ไม่ใช่เชตว่างและไม่มี
 เป็นสมาชิก จะมีไวยากรณ์ไม่พึ่งบริบท G ที่กฎการผลิตทุกกฎอยู่ในรูปแบบบรรทัดฐานชอมสกี
และ L = L(G) เป็นสมาชิก จะมีไวยากรณ์ไม่พึ่งบริบท G ที่กฎการผลิตทุกกฎอยู่ในรูปแบบบรรทัดฐานชอมสกี
และ L = L(G)
ทฤษฏีบท สำหรับไวยากรณ์ไม่พึ่งบริบท G ทุกชุดที่ไม่มีตัวแปรไร้ประโยชน์ การผลิตไร้ประโยชน์
การผลิต- และการผลิตหนึ่งหน่วย จะมีไวยากรณ์ไม่พึ่งบริบท G" ที่สมมูลกับ G
และมีสมบัติว่าการผลิตทุกแบบใน G" อยู่ในรูปแบบบรรทัดฐานกรายบาค (จีเอ็นเอฟ) และการผลิตหนึ่งหน่วย จะมีไวยากรณ์ไม่พึ่งบริบท G" ที่สมมูลกับ G
และมีสมบัติว่าการผลิตทุกแบบใน G" อยู่ในรูปแบบบรรทัดฐานกรายบาค (จีเอ็นเอฟ)
พิสูจน์ ให้ G เป็นไวยากรณ์ไม่พึ่งบริบทที่ไม่มีตัวแปรไร้ประโยชน์ การผลิตไร้ประโยชน์
การผลิต- และการผลิตหนึ่งหน่วย จากทฤษฏีบทที่กล่าวมาก่อนหน้านี้
เราสามารถสมมติโดยไม่เสียนัยว่า G อยู่ในรูปแบบบรรทัดฐานชอมสกี และการผลิตหนึ่งหน่วย จากทฤษฏีบทที่กล่าวมาก่อนหน้านี้
เราสามารถสมมติโดยไม่เสียนัยว่า G อยู่ในรูปแบบบรรทัดฐานชอมสกี
เราจะแสดงเพียงขั้นตอนวิธีในการสร้างเท่านั้น การพิสูจน์ให้ดูจาก Hopcroft and Ullman 1979
สมมติว่า G = < {A1, A2, ..., An}, T, P, A1 > และการผลิตทุกแบบใน P
อยู่ในรูปแบบซีเอ็นเอฟ
ขั้นตอนที่ 1 พิจารณากฎการผลิตใน P สร้าง P' และ V' ดังนี้
- (1.1) ใส่การผลิตทุกแบบใน P ที่อยู่ในรูปแบบ Ai
 a เมื่อ a a เมื่อ a
 T เข้าไปใน P' T เข้าไปใน P'
- (1.2) พิจารณาการผลิตทุกแบบที่เหลือใน P ที่ไม่อยู่ในรูปแบบ A
 a จะพบว่าการผลิตเหล่านั้น
ต้องอยู่ในรูปแบบ Ai a จะพบว่าการผลิตเหล่านั้น
ต้องอยู่ในรูปแบบ Ai  Aj
Aj เมื่อ เมื่อ 
 {A1, A2, ..., An} {A1, A2, ..., An}
(1.2.1) ใส่การผลิตทุกแบบที่อยู่ในแบบ Ai  Aj
Aj เมื่อ i < j เข้าไปใน P' เมื่อ i < j เข้าไปใน P'
(1.2.2) สำหรับการผลิตที่อยู่ในรูปแบบ Ai  Aj
Aj เมื่อ i > j เมื่อ i > j
เราจะจัดรูปแบบใหม่โดยเริ่มจากดรรชนี k ที่เล็กที่สุดที่ทำให้ Ak  Aj
Aj เมื่อ k > j โดยการใช้กฎที่มีดรรชนีเล็กกว่า
เราสามารถเขียนกฎใหม่จนกระทั่งได้ Ak เมื่อ k > j โดยการใช้กฎที่มีดรรชนีเล็กกว่า
เราสามารถเขียนกฎใหม่จนกระทั่งได้ Ak  Ak
Ak
เพื่อให้ไวยากรณ์ผลิตสายอักขระที่เหมือนเดิม เราทำการสร้างตัวแปรใหม่ Bk และการผลิต Bk
  | |
 Bk แทนที่กฎเก่า Ak Bk แทนที่กฎเก่า Ak
 Ak Ak
พร้อมทั้งสำหรับแต่ละ Ak 
 โดยที่ โดยที่  ไม่ขึ้นต้นด้วย
A1, ..., Ak เราใส่การผลิต Ak ไม่ขึ้นต้นด้วย
A1, ..., Ak เราใส่การผลิต Ak 
 Bk เข้าไปใน P' (กำจัด Ak Bk เข้าไปใน P' (กำจัด Ak
 Ak Ak ออก) ออก)
- ทำซ้ำ (1.2.2) จนไม่มีรูปแบบ Ai
 Aj
Aj ที่ i > j เกิดขึ้นอีก ที่ i > j เกิดขึ้นอีก
เราได้ว่าการผลิตใน P' ที่เป็นไปได้อยู่ในรูปแบบดังต่อไปนี้เท่านั้น
- Ai
 Aj
Aj เมื่อ i < j เมื่อ i < j
- Ai
 a a
- Bi
 
ขั้นตอนที่ 2 เขียนแทนการผลิตที่ไม่อยู่ในรูปแบบของกรายบาค ด้วยการผลิตในรูปของจีเอ็นเอฟ
- (2.1) การผลิตใน P' ที่อยู่ในรูปแบบ An

 โดยที่ โดยที่  ขึ้นต้นด้วยคำปลายทาง
ให้เก็บใน P" ขึ้นต้นด้วยคำปลายทาง
ให้เก็บใน P"
- (2.2) การผลิตใน P' ที่อยู่ในรูปแบบ An-1

 โดยที่ โดยที่  ขึ้นด้วยคำปลายทาง
ให้เก็บใน P" หรือ An-1 ขึ้นด้วยคำปลายทาง
ให้เก็บใน P" หรือ An-1  An
An 1 ให้แทน An ด้วยรูปแบบการผลิตของกรายบาค
ที่ได้มาก่อนหน้านี้แล้วเก็บใน P" 1 ให้แทน An ด้วยรูปแบบการผลิตของกรายบาค
ที่ได้มาก่อนหน้านี้แล้วเก็บใน P"
- ทำซ้ำกับ (2.2) สำหรับ An-2, ..., A1
สำหรับการผลิตในรูปแบบของตัวแปรใหม่ Bi  a
a ให้เก็บใน P" หรือ Bi ให้เก็บใน P" หรือ Bi
 Aj Aj 1
ให้แทน Aj ด้วยรูปแบบการผลิตของกรายบาคที่ได้จากข้างต้น แล้วใส่การผลิตใน P" 1
ให้แทน Aj ด้วยรูปแบบการผลิตของกรายบาคที่ได้จากข้างต้น แล้วใส่การผลิตใน P"
เราจะได้ G" = < V', T, P", A1 > เป็นไวยากรณ์ไม่พึ่งบริบทที่การผลิตทุกแบบอยู่ในรูปแบบบรรทัดฐานกรายบาค และ L(G) = L(G")
บทแทรก สำหรับทุกภาษาไม่พึ่งบริบท L ที่ไม่ใช่เซตว่างและไม่มี
 เป็นสมาชิก จะมีไวยากรณ์ไม่พึ่งบริบท G" ที่การผลิตทุกแบบอยู่ในรูปแบบบรรทัดฐานกรายบาคที่ L = L(G") เป็นสมาชิก จะมีไวยากรณ์ไม่พึ่งบริบท G" ที่การผลิตทุกแบบอยู่ในรูปแบบบรรทัดฐานกรายบาคที่ L = L(G")
ตัวอย่างที่ 2: ให้ G = < {S, A, B}, {a, b}, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทที่มีเซตของการผลิต P ประกอบไปด้วย
S  AB, A AB, A  BS | b, B BS | b, B
 SA | a SA | a
จงหาไวยากรณ์ไม่พึ่งบริบท G" ที่การผลิตทั้งหมดอยู่ในรูปแบบจีเอ็นเอฟที่สมมูลกับ G
วิธีทำ ให้ A1 แทน S, A2 แทน A, A3 แทน B เขียนกฎการผลิตใหม่ได้เป็น
- A1
 A2A3,
A2 A2A3,
A2  A3A1 | b,
A3 A3A1 | b,
A3  A1A2 | a A1A2 | a
ขั้นตอนที่ 1: พิจารณากฎการผลิตใน P สร้างเซต P' และ V' ใหม่ดังนี้
- (1.1) ใส่ A2
 b, A3 b, A3
 a เข้าใน P' a เข้าใน P'
- (1.2.1) เติม A1
 A2A3, A2 A2A3, A2
 A3A1 เข้าใน P' จะได้ P' = {A1 A3A1 เข้าใน P' จะได้ P' = {A1
 A2A3, A2 A2A3, A2
 A3A1 | b, A3 A3A1 | b, A3
 a } a }
- (1.2.2) จัดรูปแบบ A3
 A1A2 ใหม่โดยใช้กฎใน P' ได้ A1A2 ใหม่โดยใช้กฎใน P' ได้
A3  A2A3A2 (โดยใช้
A1 A2A3A2 (โดยใช้
A1  A2A3) แล้วตามด้วย A2A3) แล้วตามด้วย
A3  A3A1A3A2 |
bA3A2 (โดยใช้ A2 A3A1A3A2 |
bA3A2 (โดยใช้ A2  A3A1 | b)
A3A1 | b)
เนื่องจากเรามีกฎการแปลงที่มี A3 ปรากฎซ้ำเป็นตัวแรกทางขวาคือ A3
 A3A1A3A2
เราเพิ่มตัวแปร B3 ใน V' และใส่การผลิต B3 A3A1A3A2
เราเพิ่มตัวแปร B3 ใน V' และใส่การผลิต B3  A1A3A2 | A1A3A2B3 เข้าใน P'
(ในกรณีนี้
A1A3A2 | A1A3A2B3 เข้าใน P'
(ในกรณีนี้  = A1A3A2) = A1A3A2)
เนื่องจาก A3  bA3A2 | a
เป็นการผลิตที่ไม่ขึ้นด้วย Aj ที่ j bA3A2 | a
เป็นการผลิตที่ไม่ขึ้นด้วย Aj ที่ j  3 เราจึงต้องเปลี่ยนการผลิตของ A3 ได้เป็น 3 เราจึงต้องเปลี่ยนการผลิตของ A3 ได้เป็น
A3  bA3A2B3 |
bA3A2 | aB3 | a (เราสามารถตัดกฎ A3 bA3A2B3 |
bA3A2 | aB3 | a (เราสามารถตัดกฎ A3
 A3A1A3A2
ออกจากการพิจารณาได้) A3A1A3A2
ออกจากการพิจารณาได้)
ขั้นตอนที่ 2: เราเขียนการผลิตใหม่ได้ G" = < {A1, A2, A3,
B3}, {a, b}, P", A1 > โดยที่ P" ประกอบด้วย
- A3
 bA3A2B3 |
bA3A2 | aB3 | a, bA3A2B3 |
bA3A2 | aB3 | a,
- A2
 bA3A2B3A1 |
bA3A2A1 | aB3A1 | aA1 | b,
bA3A2B3A1 |
bA3A2A1 | aB3A1 | aA1 | b,
- A1
 bA3A2B3A1A3 |
bA3A2A1A3 | aB3A1A3 |
aA1A3 | bA3,
bA3A2B3A1A3 |
bA3A2A1A3 | aB3A1A3 |
aA1A3 | bA3,
- B3
 bA3A2B3A1A3A3A2 |
bA3A2A1A3A3A2 |
aB3A1A3A3A2 | aA1A3A3A2
| bA3A3A2 |
bA3A2B3A1A3A3A2B3 |
bA3A2A1A3A3A2B3 |
aB3A1A3A3A2B3 |
aA1A3A3A2B3 |
bA3A3A2B3
bA3A2B3A1A3A3A2 |
bA3A2A1A3A3A2 |
aB3A1A3A3A2 | aA1A3A3A2
| bA3A3A2 |
bA3A2B3A1A3A3A2B3 |
bA3A2A1A3A3A2B3 |
aB3A1A3A3A2B3 |
aA1A3A3A2B3 |
bA3A3A2B3
ตัวอย่างที่ 3: ให้ G = <{A1, A2, A3}, {a, b}, P, A1 >
เป็นไวยากรณ์ไม่พึ่งบริบทชุดหนึ่งเมื่อ P ประกอบด้วย A1  A2A2A3, A2
A2A2A3, A2  A1A2 | b, A3
A1A2 | b, A3  A1A3 | a | A1A3 | a |

จงหาไวยากรณ์ไม่พึ่งบริบท G" ที่การผลิตทุกแบบอยู่ในรูปของกรายบาคและสมมูลกับ G
สมบัติของภาษาไม่พึ่งบริบท
ภาษาไม่พึ่งบริบท เป็นกลุ่มของภาษาที่ใหญ่กว่าภาษาปกติ นั่นคือสำหรับภาษาปกติทุกภาษา
เราสามารถเขียนไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิดภาษาปกตินั้นได้เสมอ โดยเราจะใช้ทฤษฎีบทต่อไปนี้ในการพิสูจน์
ทฤษฎีบท - ถ้า L1 และ L2 เป็นภาษาไม่พึ่งบริบทแล้ว
L1
 L2 และ L1L2 เป็นภาษาไม่พึ่งบริบทด้วย L2 และ L1L2 เป็นภาษาไม่พึ่งบริบทด้วย
- ถ้า L เป็นภาษาไม่พึ่งบริบทแล้ว L* เป็นภาษาไม่พึ่งบริบทด้วย
พิสูจน์- ให้ G1 = < V1, T1, P1, S1 >
เป็นไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด L1 และ ให้ G2 = < V2, T2, P2,
S2 > เป็นไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด L2 โดยที่ V1 และ V2 ไม่มีตัวแปรร่วมกันเลย
เราเขียนไวยากรณ์ไม่พึ่งบริบทใหม่ได้เป็น G = < V1  V2 V2
 {S}, T1 {S}, T1  T2,
P1 T2,
P1  P2 P2  {S
{S  S1 | S2} , S > เป็นไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด
L1 S1 | S2} , S > เป็นไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด
L1  L2 L2
และ ไวยากรณ์ไม่พึ่งบริบท G' = < V1  V2 V2
 {S}, T1 {S}, T1  T2,
P1 T2,
P1  P2 P2  {S
{S  S1S2} , S > เป็นไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด
L1L2 S1S2} , S > เป็นไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด
L1L2
- ให้ G = < V, T, P, S > เป็นไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด L
สร้าง G' = < V  {S'}, T, P {S'}, T, P  {S'
{S'  SS' | SS' |  }, S' >
เป็นไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด L* }, S' >
เป็นไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด L*
ตัวอย่างที่ 4 จงแสดงว่า  ,
{ ,
{ }, {a} เป็นภาษาไม่พึ่งบริบทเมื่อ a }, {a} เป็นภาษาไม่พึ่งบริบทเมื่อ a 

ดังนั้น ภาษาปกติเป็นภาษาไม่พึ่งบริบทด้วย
หมายเหตุ L1  L2 อาจไม่เป็นภาษาไม่พึ่งบริบท
แม้ว่าทั้ง L1 และ L2 เป็นภาษาไม่พึ่งบริบทก็ตาม เช่น L2 อาจไม่เป็นภาษาไม่พึ่งบริบท
แม้ว่าทั้ง L1 และ L2 เป็นภาษาไม่พึ่งบริบทก็ตาม เช่น
L1 = {ambncn | m, n 
 } และ L2 = {ambmcn | m, n } และ L2 = {ambmcn | m, n
  } เป็นภาษาไม่พึ่งบริบททั้งคู่ } เป็นภาษาไม่พึ่งบริบททั้งคู่
แต่ L1  L2 =
{anbncn | n L2 =
{anbncn | n 
 } ไม่ใช่ภาษาไม่พึ่งบริบท } ไม่ใช่ภาษาไม่พึ่งบริบท
ไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด L1 คือ < {S, A, B}, {a, b, c}, {S  AB,
A AB,
A  aA | a, B aA | a, B  bBc | bc}, S > bBc | bc}, S >
ไวยากรณ์ไม่พึ่งบริบทที่ก่อกำเนิด L2 คือ < {S', C, D}, {a, b, c}, {S'  CD,
C CD,
C  aCb | ab, D aCb | ab, D  cD | c}, S' > cD | c}, S' >
เราพบว่าภาษาไม่พึ่งบริบทก็ยังไม่ครอบคลุมภาษาทั้งหมดที่เราสนใจ นั่นคือยังมีภาษาบางภาษาที่ไม่ใช่ภาษาไม่พึ่งบริบท
ซึ่งเราสามารถแสดงการพิสูจน์โดยใช้ทฤษฎีบทตั้งการปั๊มขึ้นมาสำหรับภาษาไม่พึ่งบริบทที่จะกล่าวต่อไป
ทฤษฎีบทตั้งการปั๊มขึ้นมาสำหรับภาษาไม่พึ่งบริบท (Pumping lemma for CFL)
ถ้า L   *
เป็นภาษาไม่พึ่งบริบท แล้วจะได้ว่า จะมีจำนวนเต็มบวก k ที่มีสมบัติว่า *
เป็นภาษาไม่พึ่งบริบท แล้วจะได้ว่า จะมีจำนวนเต็มบวก k ที่มีสมบัติว่า
- (**) สำหรับทุก z

 * ถ้า z * ถ้า z  L และ
| z | L และ
| z | 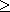 k แล้ว เราสามารถเขียน z = uvwxy ได้โดยที่
u, v, w, x, y k แล้ว เราสามารถเขียน z = uvwxy ได้โดยที่
u, v, w, x, y 
 *,
| vx | *,
| vx | 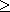 1, | vwx | 1, | vwx |  k และ
uviwxiy k และ
uviwxiy  L ทุก i L ทุก i
  0 0
ตัวอย่างที่ 5: จงพิสูจน์ว่า L = {anbncn | n
  } ไม่ใช่ภาษาไม่พึ่งบริบท } ไม่ใช่ภาษาไม่พึ่งบริบท
พิสูจน์ สมมติว่า L เป็นภาษาไม่พึ่งบริบท ดังนั้นโดย ทฤษฎีบทประกอบการปั๊มขึ้นมาสำหรับภาษาไม่พึ่งบริบท จะได้ว่า
จะมีจำนวนเต็มบวก k ที่สอดคล้องกับสมบัติ (**) ในทฤษฎี
ถ้าเราพิจารณา z = akbkck ได้ว่า z  L
และ | z | = k + k + k = 3k L
และ | z | = k + k + k = 3k 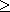 k ทำให้เงื่อนไขใน (**) เป็นจริง k ทำให้เงื่อนไขใน (**) เป็นจริง
เราเขียน akbkck = z = uvwxy ได้โดยที่ 1
 | vx |, | vwx | | vx |, | vwx |  k และ
uviwxiy k และ
uviwxiy  L
ทุกจำนวนเต็ม i L
ทุกจำนวนเต็ม i 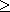 0 0
ถ้าพิจารณาที่ i = 0 จะได้ว่า uwy  L L
จาก | vx | 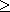 1, | vwx | 1, | vwx |  k
และ akbkck = uvwxy เราอาจได้ว่า vx = ambj โดยที่ 1 k
และ akbkck = uvwxy เราอาจได้ว่า vx = ambj โดยที่ 1
 j + m j + m  k
หรือ vx = bsct โดยที่ 1 k
หรือ vx = bsct โดยที่ 1  s + t s + t
 k k
กรณีที่ 1: vx = ambj โดยที่ 1  j + m j + m
 k จะได้ว่า uwy = ak-mbk-jck ซึ่งไม่อยู่ใน L
(จำนวนของตัวอักขระ a, b, c ต้องเท่ากันเท่านั้น) k จะได้ว่า uwy = ak-mbk-jck ซึ่งไม่อยู่ใน L
(จำนวนของตัวอักขระ a, b, c ต้องเท่ากันเท่านั้น)
กรณีที่ 2: vx = bsct โดยที่ 1  s + t s + t
 k จะได้ว่า uwy = akbk-sck-t ซึ่งไม่อยู่ใน L
(จำนวนของตัวอักขระ a, b, c ต้องเท่ากันเท่านั้น) k จะได้ว่า uwy = akbk-sck-t ซึ่งไม่อยู่ใน L
(จำนวนของตัวอักขระ a, b, c ต้องเท่ากันเท่านั้น)
ไม่ว่ากรณีใดๆ เกิดการขัดแย้งเสมอ ข้อความที่สมมติไว้ไม่เป็นจริง ดังนั้น L ไม่เป็นภาษาไม่พึ่งบริบท
ข้อสังเกตุ ภาษาบางภาษาไม่เป็นภาษาไม่พึ่งบริบท เช่น L = {atbjcmdn | t = 0 หรือ
j = m = n เพียงอย่างใดอย่างหนึ่ง} แต่เราไม่สามารถใช้ทฤษฎีบทตั้งการปั๊มขึ้นมาสำหรับภาษาไม่พึ่งบริบทในการพิสูจน์ได้ ซึ่งเราต้องใช้
ทฤษฎีบทที่แสดงสมบัติของภาษาไม่พึ่งบริบทที่ดีกว่าทฤษฎีบทตั้งการปั๊มขึ้นมาสำหรับภาษาไม่พึ่งบริบทที่เรียกว่า ทฤษฎีบทตั้งของอ๊อคเดน (Ogden's Lemma)
ซึ่งต้องใช้ความหมายของการแยกแยะได้ เราจึงจะข้ามการใช้ทฤษฎีนี้ไป
ทฤษฎีบทตั้งของอ๊อคเดน (Ogden's lemma)
ถ้า L   *
เป็นภาษาไม่พึ่งบริบท แล้วจะได้ว่า จะมีจำนวนเต็มบวก k ที่มีสมบัติว่า *
เป็นภาษาไม่พึ่งบริบท แล้วจะได้ว่า จะมีจำนวนเต็มบวก k ที่มีสมบัติว่า
- (***) สำหรับทุก z

 * ถ้า z * ถ้า z  L แล้ว
สำหรับทุกการกำหนด "ตำแหน่งแยกแยะ" อย่างน้อย k ตำแหน่งใน z จะได้ว่าเราสามารถเขียน z = uvwxy ได้โดยที่
u, v, w, x, y L แล้ว
สำหรับทุกการกำหนด "ตำแหน่งแยกแยะ" อย่างน้อย k ตำแหน่งใน z จะได้ว่าเราสามารถเขียน z = uvwxy ได้โดยที่
u, v, w, x, y 
 * และ * และ
- v และ x รวมกันต้องมีตำแหน่งแยกแยะอย่างน้อยหนึ่งตำแหน่ง
- vwx มีตำแหน่งแยกแยะไม่เกิน k ตำแหน่ง และ
- uviwxiy
 L ทุก i L ทุก i
  0 0
การสมมูลกันของออโตมาตากดลง
เราทราบความแตกต่างระหว่างเครื่องออโตมาตากดลงทั้งแบบเชิงกำหนดและเชิงไม่กำหนด
ในส่วนนี้เราสนใจกลุ่มของภาษาที่ยอมรับได้โดยออโตมาตากดลงแบบปกติ (ประโยคที่ยอมรับโดยการหยุดที่สถานะยอมรับ)
กับแบบที่ยอมรับโดยกองซ้อนว่างซึ่งเราจะแสดงว่ากลุ่มภาษาทั้งสองนี้สมมูลกัน ต่อจากนั้นเราจึงค่อยแสดงว่า
กลุ่มของภาษาที่ยอมรับด้วยออโตมาตากดลงแบบกองซ้อนว่างสมมูลกับกลุ่มของภาษาไม่พึ่งบริบท
ทฤษฎีบท L เป็นภาษาที่ยอมรับโดยสถานะยอมรับของออโตมาตากดลง M1 ก็ต่อเมื่อ L
เป็นภาษาที่ยอมรับโดยกองซ้อนว่างของออโตมาตากดลง M2
พิสูจน์
- ให้ L เป็นภาษาที่ยอมรับโดยสถานะยอมรับของออโตมาตากดลง M = (Q,
 , ,
 , ,  , q0, Z0, F) , q0, Z0, F)
เราสร้างออโตมาตาแบบกดลงที่ยอมรับโดยกองซ้อนว่างได้ดังนี้ M' = (Q  {q', q"}, {q', q"},
 , , 
 {Z'0}, {Z'0},  ',
q', Z'0, ',
q', Z'0,  ) เป็นออโตมาตากดลงที่มีนิยามของ ) เป็นออโตมาตากดลงที่มีนิยามของ
 ' ดังนี้ ' ดังนี้
-
 '(q', '(q',  , Z'0) =
{(q0, Z0Z'0) } หมายถึงเมื่อเริ่มต้น เราใส่สัญลักษณ์ของกองซ้อนตัวล่างสุดของเครื่อง M บนสัญลักษณ์กองซ้อนว่างของ M' ก่อน) , Z'0) =
{(q0, Z0Z'0) } หมายถึงเมื่อเริ่มต้น เราใส่สัญลักษณ์ของกองซ้อนตัวล่างสุดของเครื่อง M บนสัญลักษณ์กองซ้อนว่างของ M' ก่อน)
 '(q, a, A) = '(q, a, A) =  (q, a, A)
ทุก q (q, a, A)
ทุก q  Q - F, a Q - F, a 
  {
{ }, A }, A 

 '(q, '(q,  , A) = , A) =
 (q, (q,  , A) , A)
 {(q", {(q",  )} ทุก q )} ทุก q
 F, A F, A 

 '(q", '(q",  , A) = {(q", , A) = {(q",
 )} ทุก A )} ทุก A 
  {Z'0} {Z'0}
โดยที่ในขั้นที่ 1 บ่งบอกว่าเริ่มต้นของ M' ให้เปลี่ยนเป็นสถานะเริ่มต้นของ M และใส่สัญลักษณ์กองซ้อนว่างของ M บนสัญลักษณ์กองซ้อนว่างของ M'
ในขั้นที่ 2 ให้ทำงาน M' เหมือนกับ M ยกเว้นกรณีที่อยู่ในสถานะยอมรับใน F
ในขั้นที่ 3 และ 4 เป็นการทำกองซ้อนให้ว่างเมื่อเราพบว่า เราต้องการยอมรับคำปัจจุบัน
จะเห็นได้ว่า L(M) = N(M')
- ในทางกลับกัน ถ้า L ซึ่งเป็นภาษาที่ยอมรับโดยกองซ้อนว่างของออโตมาตาจำกัด M = (Q,
 , ,  , ,
 , q0, Z0, , q0, Z0,  ) )
เราสร้างออโตมาตาแบบกดลงที่ยอมรับโดยสถานะยอมรับได้ดังนี้ M' = (Q  {q',
qF}, {q',
qF},  , , 
 {Z'0}, {Z'0},  ',
q', Z'0, {qF}) เป็นออโตมาตากดลงที่มีนิยามของ ',
q', Z'0, {qF}) เป็นออโตมาตากดลงที่มีนิยามของ  ' ดังนี้ ' ดังนี้
-
 '(q', '(q',  , Z'0) =
{(q0, Z0Z'0) } หมายถึงเมื่อเริ่มต้น เราใส่สัญลักษณ์ของกองซ้อนตัวล่างสุดของเครื่อง M ก่อน) , Z'0) =
{(q0, Z0Z'0) } หมายถึงเมื่อเริ่มต้น เราใส่สัญลักษณ์ของกองซ้อนตัวล่างสุดของเครื่อง M ก่อน)
 '(q, a, A) = '(q, a, A) =  (q, a, A)
ทุก q (q, a, A)
ทุก q  Q Q  {q', qF}, a {q', qF}, a
 
 { { }, A }, A
 
 '(q, '(q,  , Z'0) =
{(qF, Z'0)} ทุก q , Z'0) =
{(qF, Z'0)} ทุก q  Q Q
โดยที่ในขั้นที่ 1 บ่งบอกว่าเริ่มต้นของ M' ให้เปลี่ยนเป็นสถานะเริ่มต้นของ M และใส่สัญลักษณ์กองซ้อนว่างของ M บนสัญลักษณ์กองซ้อนว่างของ M'
ในขั้นที่ 2 ให้ทำงาน M' เหมือนกับ M
ในขั้นที่ 3 เมื่ออ่านสายอักขระจนจบ และถ้าในกองซ้อนของ M' เหลืออยู่แค่ Z'0 ให้ย้ายสถานะไปยังสถานะยอมรับ
จะเห็นได้ว่า N(M) = L(M')
ทฤษฏีบท ถ้า L เป็นภาษาไม่พึ่งบริบท แล้วจะมีเครื่องออโตมาตากดลง M ที่ L = N(M)
พิสูจน์ สมมติให้ L เป็นภาษาไม่พึ่งบริบท
ในกรณีที่ L =  หรือ L = { หรือ L = { }
จะเห็นได้ง่ายว่า เราสามารถสร้างออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่างได้ที่ L = N(M) }
จะเห็นได้ง่ายว่า เราสามารถสร้างออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่างได้ที่ L = N(M)
ดังนั้นเราจะพิจารณาในกรณีที่ L   และ L
และ L  { { }
ให้ L' = L - { }
ให้ L' = L - { } เราได้ว่า L' เป็นภาษาไม่พึ่งบริบทด้วย โดยทฤษฎีบทที่ผ่านมาจะได้ว่า
เรามีไวยากรณ์ไม่พึ่งบริบทที่อยู่ในรูปกรายบาคที่ L' = L(G) โดยที่ G = < V, T, P, S > เราสร้าง M =
(Q, } เราได้ว่า L' เป็นภาษาไม่พึ่งบริบทด้วย โดยทฤษฎีบทที่ผ่านมาจะได้ว่า
เรามีไวยากรณ์ไม่พึ่งบริบทที่อยู่ในรูปกรายบาคที่ L' = L(G) โดยที่ G = < V, T, P, S > เราสร้าง M =
(Q,  , ,  , ,
 , q0, Z0, , q0, Z0,  ) )
- Q = {q0, q1}
 = T = T = V = V  {Z0} {Z0} นิยามดังนี้ นิยามดังนี้  (q0, (q0,
 , Z0) = {(q1, S)} , Z0) = {(q1, S)}
และสำหรับทุก a  T, A T, A  V, V,
  V*
(q1, V*
(q1,  ) )  , ,
 (q1, a, A) ก็ต่อเมื่อ A (q1, a, A) ก็ต่อเมื่อ A  a
a เป็นการผลิตใน P เป็นการผลิตใน P
จะได้ว่า L' = N(M) การขยายไปสู่การยอมรับ L ที่มี  ก็สามารถทำได้โดยง่าย ก็สามารถทำได้โดยง่าย
ตัวอย่างที่ 6: จงสร้างออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่าง สำหรับ L =
{ambncn | m, n 
 } }
ตัวอย่างที่ 7: จงสร้างออโตมาตากดลงที่ยอมรับโดยกองซ้อนว่าง ที่ยอมรับ L(G) โดยที่ G =
< {S, A, B}, {0, 1}, P, S > และ P = { S  0SA | 0A, A 0SA | 0A, A
 1AB | 10, B 1AB | 10, B  0} 0}
ทฤษฏีบท ถ้า L เป็นภาษาที่มีเครื่องออโตมาตากดลง M ที่ยอมรับ L โดยกองซ้อนว่าง แล้ว L ต้องเป็นภาษาไม่พึ่งบริบท
พิสูจน์ ให้ L เป็นภาษาที่ยอมรับโดยเครื่องออโตมาตากดลง M = (Q,  , ,
 , ,  , q0, Z0, , q0, Z0,
 ) นั่นคือ L = N(M) ) นั่นคือ L = N(M)
เราสร้างไวยากรณ์ไม่พึ่งบริบทดังนี้ G = < V, T, P, S >
- V = {[q, A, p] } q, p
 Q, A Q, A 
 } }  {S} {S}
- T =

- P เป็นเซตของการผลิตต่อไปนี้
- S
 [q0, Z0, q] ทุก q [q0, Z0, q] ทุก q
 Q Q
- [q, A, q1]
 a ถ้า (q1, a ถ้า (q1,
 ) ) 
 (q, a, A) ทุก q, q1 (q, a, A) ทุก q, q1  Q,
a Q,
a  
 { { }, A }, A
 
- [q, A, qm+1]
 a[q1, B1, q2]
[q2, B2, q3] ... [qm, Bm, qm+1] ถ้า (q1,
B1B2...Bm) a[q1, B1, q2]
[q2, B2, q3] ... [qm, Bm, qm+1] ถ้า (q1,
B1B2...Bm) 
 (q, a, A) ทุก q, q1, q2, ..., qm+1 (q, a, A) ทุก q, q1, q2, ..., qm+1
 Q, a Q, a 
  {
{ }, A, B1, B2, ..., Bm }, A, B1, B2, ..., Bm
 
ตัวอย่างที่ 9: ให้ M = ({q0, q1}, {0, 1}, {X, Z0},
 , q0, Z0, , q0, Z0,  )
เป็นออโตมาตากดลงที่มี )
เป็นออโตมาตากดลงที่มี  ดังนี้ ดังนี้
 (q0, 0,
Z0) = {(q0, XZ0)}, (q0, 0,
Z0) = {(q0, XZ0)}, |
 (q0, 0, X) = {(q0, XX)}, (q0, 0, X) = {(q0, XX)}, |
 (q0, 1, X) = {(q1, (q0, 1, X) = {(q1,
 )}, )}, |
 (q1, 1,
X) = {(q1, (q1, 1,
X) = {(q1,  )}, )}, |
 (q1, (q1,  , X) =
{(q1, , X) =
{(q1,  )}, )}, |
 (q1, (q1,  , Z0) =
{(q1, , Z0) =
{(q1,  )} )} |
จงหาไวยากรณ์ไม่พึ่งบริบท G ที่ L(G) = N(M) โดยวิธีการสร้างในการพิสูจน์ทฤษฎีบท
วิธีทำ G = < V, T, P, S > โดยที่
- V = {S, [q0, X, q0], [q0, X, q1], [q1, X, q0],
[q1, X, q1], [q0, Z0, q0], [q0, Z0, q1],
[q1, Z0, q0], [q1, Z0, q1]}
- T = {0, 1}
และเราจะสนใจการผลิตที่เกิดจาก S เท่านั้น ดังนั้นเราจะเริ่มจากการผลิต S ไปตัวแปรที่เหลือ จนกระทั่งถึงคำปลายทาง
- S
 [q0, Z0, q0] | [q0,
Z0, q1] [q0, Z0, q0] | [q0,
Z0, q1]
- เพิ่มการผลิตสำหรับตัวแปร [q0, Z0, q0] จาก
 (q0, 0, Z0) = {(q0, XZ0)}
(q0, 0, Z0) = {(q0, XZ0)}
[q0, Z0, q0]  0[q0, X, q0]
[q0, Z0, q0] 0[q0, X, q0]
[q0, Z0, q0]
และ [q0, Z0, q0]  0[q0, X, q1][q1, Z0, q0]
0[q0, X, q1][q1, Z0, q0]
- การผลิตสำหรับตัวแปร [q0, Z0, q1] จาก
 (q0, 0, Z0) = {(q0, XZ0)} คือ
(q0, 0, Z0) = {(q0, XZ0)} คือ
[q0, Z0, q1]  0[q0, X, q0][q0, Z0, q1]
0[q0, X, q0][q0, Z0, q1]
และ [q0, Z0, q1]  0[q0, X, q1][q1, Z0, q0]
0[q0, X, q1][q1, Z0, q0]
- จาก
 (q0, 0, X) = {(q0, XX)} จะได้การผลิตต่อไปนี้ (q0, 0, X) = {(q0, XX)} จะได้การผลิตต่อไปนี้
[q0, X, q0]  0[q0, X, q0][q0, X, q0]
0[q0, X, q0][q0, X, q0]
[q0, X, q0]  0[q0, X, q1][q1, X, q0]
0[q0, X, q1][q1, X, q0]
[q0, X, q1]  0[q0, X, q0][q0, X, q1]
0[q0, X, q0][q0, X, q1]
[q0, X, q1]  0[q0, X, q1][q1, X, q1]
0[q0, X, q1][q1, X, q1]
- จาก
 (q0, 1, X) = {(q1, (q0, 1, X) = {(q1,  )} จะได้การผลิต [q0, X, q1] )} จะได้การผลิต [q0, X, q1]  1 1
- จาก
 (q1, (q1,  ,
Z0) = {(q1, ,
Z0) = {(q1,  )} จะได้การผลิต
[q1, Z0, q1] )} จะได้การผลิต
[q1, Z0, q1] 

- จาก
 (q1, (q1,  , X) =
{(q1, , X) =
{(q1,  )} จะได้การผลิต [q1, X, q1] )} จะได้การผลิต [q1, X, q1]
 
- จาก
 (q1, 1, X) = {(q1, (q1, 1, X) = {(q1,  )} จะได้การผลิต [q1, X, q1] )} จะได้การผลิต [q1, X, q1]  1 1
เนื่องจากเราไม่มีการผลิตเกิดขึ้นสำหรับตัวแปร [q1, X, q0] และ [q1, Z0, q0] และ
การผลิตสำหรับ [q0, X, q0] และ [q0, Z0, q0] ทุกแบบมี
[q1, X, q0] และ [q1, Z0, q0] ปรากฎทางขวาเสมอ ดังนั้น
[q0, X, q0] และ [q0, Z0, q0] ไม่สามารถผลิตสายอักขระใน T* ได้
เราจึงตัดการผลิตทุกแบบที่เกี่ยวข้องกับตัวแปรทั้งสี่ออกได้ สรุปได้ว่า
- P ประกอบด้วยกฎการผลิตต่อไปนี้
- S
 [q0, Z0, q1],
[q1, Z0, q1] [q0, Z0, q1],
[q1, Z0, q1] 
 , [q0, Z0, q1] , [q0, Z0, q1]
 0[q0, X, q1][q1, Z0, q1],
[q1, X, q1] 0[q0, X, q1][q1, Z0, q1],
[q1, X, q1] 
 , [q0, X, q1] , [q0, X, q1]  0[q0, X, q1][q1, X, q1], [q1, X, q1]
0[q0, X, q1][q1, X, q1], [q1, X, q1]
 1, [q0, X, q1] 1, [q0, X, q1]
 1 1
|