เครื่องทัวริงและเครื่องทัวริงครอบจักรวาล

เครื่องทัวริงและเครื่องทัวริงครอบจักรวาล

เครื่องทัวริง (Turing Machines)
ความสามารถของเครื่องที่ศึกษามายอมรับภาษาที่มีข้อจำกัดอยู่ เช่น ภาษาปกติ (โดยออโตมาตาจำกัด) ภาษาไม่พึ่งบริบท (โดยออโตมาตากดลง) ในขั้นต่อไปเราจะสร้างเครื่องที่สามารถยอมรับภาษาอื่นที่เครื่องเหล่านั้นยอมรับไม่ได้ เรียกว่าเครื่องทัวริง เครื่องทัวริงถูกคิดค้นครั้งแรกโดย อลัน ทัวริง (Alan Turing) ในปี ค.ศ. 1936 โดยที่หลักการของเครื่องนี้ถือได้ว่าเป็นแม่แบบของสถาปัตยกรรมของเครื่องคอมพิวเตอร์ที่มีหน่วยประมวลผลเดี่ยว ในปัจจุบันเครื่องทัวริงสามารถแบ่งออกได้เป็น

เครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียว (One-way infinite single tape Turing machine),
เครื่องทัวริงแถบเดี่ยวปลายเปิดสองทาง (Two-way infinite single tape Turing machine)
หรือ เครื่องทัวริงหลายแถบ (Multitape Turing machine)

ตามจำนวนแถบและการใช้งานแถบ ในยุคแรกทัวริงออกแบบเครื่องในลักษณะของเครื่องทัวริงแถบเดี่ยวปลายเปิดสองทาง แต่เพื่อความง่ายต่อการเข้าใจ เราจะเริ่มศึกษาเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียวก่อน แล้วค่อยพิจารณาเครื่องทัวริงที่ใช้แถบเดี่ยวปลายเปิดสองทาง และเครื่องทัวริงหลายแถบ ไม่ว่าอย่างไรก็ตามเราสามารถแสดงได้ว่าเครื่องทัวริงทั้งหมดสมมูลกัน

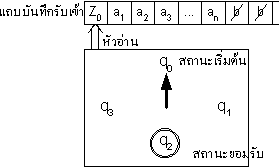
บทนิยาม เครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียว (One-way infinite single tape Turing machine) แต่ละเครื่องประกอบด้วย

เซตของสถานะ (state) ทั้งหมดซึ่งเป็นเซตจำกัด เขียนแทนด้วย Q
เซตของสัญลักษณ์รับเข้า (input symbol) ทั้งหมดซึ่งเป็นเซตจำกัด เขียนแทนด้วย
เซตของสัญลักษณ์แถบ (tape symbol) ทั้งหมดซึ่งเป็นเซตจำกัด เขียนแทนด้วย สังเกตว่า
เซตของสถานะยอมรับ (accepting state) ทั้งหมดซึ่งเป็นสับเซตของ Q เขียนแทนด้วย F
สถานะเริ่มต้น (initial state) ซึ่งเป็นสมาชิกใน Q เขียนแทนด้วย q₀
สัญลักษณ์พิเศษที่บอกตำแหน่งซ้ายสุดของแถบ เขียนแทนด้วย Z₀ และสัญลักษณ์ที่บอกว่าไม่มีข้อมูลบันทึกในช่อง เขียนแทนด้วย โดยที่ Z₀ ไม่ใช่ตัวเดียวกับ
ฟังก์ชันการผ่าน (transition function) เป็นฟังก์ชันที่มีโดเมนเป็นสับเซตของ Q × และพิสัยเป็นสับเซตของ Q × × {R, L, S} และมีเงื่อนไขว่า
(q_f, i) ไม่มีค่าทุก q_f F, i

และถ้า (q, Z₀) = (p, X, D) แล้ว D L และ X = Z₀

บทนิยาม แผนภาพการผ่าน (transition diagram) ของเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียว (Q,

, q₀, Z₀, F) คือ กราฟเทียมที่มีทิศทาง มี Q เป็นเซตของจุดยอด มีลูกศรชี้เข้าที่จุดยอด q₀ จุดยอดทุกจุดใน F มีวงกลมล้อมรอบสองวง และถ้า

(q, a) = (p, X, D) แล้วจะต้องมีอาร์กเชื่อมจากจุดยอด q ไปยังจุดยอด p โดยมี (a), (X, D) เขียนกำกับ ดังรูป

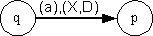
ตัวอย่างที่ 1: จงเขียนแผนภาพการผ่านของเครื่องทัวริง M = (Q,

, q₀, Z₀, F) โดยที่ Q = {q₀, q₁, q₂},

= {0, 1},

= {0, 1, X, Z₀,

}, F = {q₁} และ

(q₀, Z₀) = (q₀, Z₀, R),

(q₀, 0) = (q₁, X, R),

(q₀, 1) = (q₂, 1, R),

(q₂, 0) = (q₁, X, R),

(q₂, 1) = (q₀, 1, R)

บทนิยาม สำหรับเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียว M = (Q,

, q₀, Z₀, F) เรากล่าวว่า c เป็น โครงแบบ (configuration) หนึ่งของเครื่องทัวริง M ก็ต่อเมื่อ c = (q,

) โดยที่ q

^*, i

และ

^*
ซึ่งหมายความว่า ขณะนั้นเครื่องทัวริง M กำลังอยู่ในสถานะ q สายอักขระที่ปรากฎบนแถบคือ

(อาจจะไม่ใช่สายอักขระรับเข้า) และหัวอ่านชี้อยู่ที่ i ดังรูป

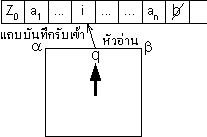
เรากล่าวว่า c เป็นโครงแบบเริ่มต้น (initial configuration) ก็ต่อเมื่อ c = (q₀,

Z₀w) เมื่อ w เป็นสายอักขระรับเข้า โดยทั่วไปจะใช้สัญลักษณ์ c₀ แทนโครงแบบเริ่มต้น
เรากล่าวว่า c เป็นโครงแบบหยุด (halting configuration) ก็ต่อเมื่อ c = (q,

) โดยที่

(q, i) ไม่มีค่า
ถ้า c = (q,

) และ c' = (q',

') ต่างก็เป็นโครงแบบของเครื่องทัวริง M และ

(q, i) = (p, X, D) แล้ว เรากล่าวว่า c' เป็นโครงแบบถัดจาก c เขียนแทนด้วย c

c' ก็ต่อเมื่อ p = q' และ

ถ้า D = R แล้ว ' = X และ = i'
ถ้า D = L แล้ว = 'i' และ = X
ถ้า D = S แล้ว ' = , = และ i' = X

เรากล่าวว่า c' เป็นโครงแบบที่ได้มาจาก c เขียนแทนด้วย c

c' ก็ต่อเมื่อ c = c' หรือ มีโครงแบบ c₁, c₂, ..., c_n ที่ c = c₁, c' = c_n และ c₁

c₂, c₂

c₃, ..., c_n-1

c_n
บทนิยาม ให้ M เป็นเครื่องทัวริงและ w เป็นสายอักขระรับเข้า จะกล่าวว่า M ยอมรับ w ก็ต่อเมื่อ มีโครงแบบ c ที่ c₀

c โดยที่สถานะที่ปรากฎในโครงแบบ c เป็นสถานะหนึ่งที่เป็นสถานะยอมรับ
ภาษาที่ M ยอมรับ เขียนแทนด้วย L(M) คือเซตของสายอักขระรับเข้าทั้งหมดที่ M ยอมรับ จะได้ L(M) = { w

^* | M ยอมรับ w }
สำหรับภาษา L ใดๆ เรากล่าวว่า M ยอมรับ L ก็ต่อเมื่อ L = L(M)
ตัวอย่างที่ 2 จงตรวจสอบว่า เครื่องทัวริงในตัวอย่างที่ 1 ยอมรับสายอักขระต่อไปนี้หรือไม่

010
1101

ตัวอย่างที่ 3 จงเขียนแผนภาพการผ่านของเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียวที่ยอมรับ L เมื่อ

L = { w {0,1}^* | w มี 0 ปรากฎอย่างน้อยหนึ่งตัว }
L = {0ⁿ1ⁿ | n }
L = { ww^R | w {0, 1}^* }
L = { ww | w {0, 1}^* }

บทนิยาม เครื่องทัวริงแถบเดี่ยวปลายเปิดสองทาง (Two-way infinite single tape Turing machine) แต่ละเครื่องประกอบด้วย

เซตของสถานะ (state) ทั้งหมดซึ่งเป็นเซตจำกัด เขียนแทนด้วย Q
เซตของสัญลักษณ์รับเข้า (input symbol) ทั้งหมดซึ่งเป็นเซตจำกัด เขียนแทนด้วย
เซตของสัญลักษณ์แถบ (tape symbol) ทั้งหมดซึ่งเป็นเซตจำกัด เขียนแทนด้วย สังเกตว่า
เซตของสถานะยอมรับ (accepting state) ทั้งหมดซึ่งเป็นสับเซตของ Q เขียนแทนด้วย F
สถานะเริ่มต้น (initial state) ซึ่งเป็นสมาชิกใน Q เขียนแทนด้วย q₀
ฟังก์ชันการผ่าน (transition function) เป็นฟังก์ชันที่มีโดเมนเป็นสับเซตของ Q × และพิสัยเป็นสับเซตของ Q × × {R, L, S} และมีเงื่อนไขว่า (q, i) ไม่มีค่าทุก q F, i

แต่มีเงื่อนไขเพิ่มเติมว่าขณะเริ่มต้นจะอยู่ในสถานะ q₀ อ่านสายอักขระรับเข้าเริ่มจากตัวที่อยู่ซ้ายสุดของสายอักขระนั้น โดยทั่วไปจะเขียนแทนเครื่องทัวริงนี้ด้วย (Q,

, q₀, F)
บทนิยาม แผนภาพการผ่าน (transition diagram) ของเครื่องทัวริงแถบเดี่ยวปลายเปิดสองทาง (Q,

, q₀, F) จะเหมือนกับของเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียว คือ กราฟเทียมที่มีทิศทาง มี Q เป็นเซตของจุดยอด มีลูกศรชี้เข้าที่จุดยอด q₀ จุดยอดทุกจุดใน F มีวงกลมล้อมรอบสองวง และถ้า

(q, a) = (p, X, D) แล้วจะต้องมีอาร์กเชื่อมจากจุดยอด q ไปยังจุดยอด p โดยมี (a), (X, D) เขียนกำกับ
นิยามของโครงแบบ โครงแบบเริ่มต้น โครงแบบหยุด โครงแบบถัดจาก และโครงแบบที่ได้มาจากคำ ของเครื่องทัวริงแถบเดี่ยวปลายเปิดสองทาง เหมือนกับเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียว
ตัวอย่างที่ 4 จงเขียนแผนภาพการผ่านของเครื่องทัวริงแถบเดี่ยวปลายเปิดสองทางที่ยอมรับ L เมื่อ L = { w

{0,1}^* | n(0, w) = n(1, w) }
บทนิยาม เครื่องทัวริง k-แถบ (k-tape Turing machine) แต่ละเครื่องประกอบด้วย (Q,

, q₀, Z₀, F) โดยที่ฟังก์ชันการผ่าน (transition function)

เป็นฟังก์ชันที่มีโดเมนเป็นสับเซตของ Q × (

{

}) ×

Q ×

^k × {R, L, S}^k+1 โดยที่

(q, a, x₁, x₂, ..., x_k) ไม่มีค่าทุก q

F, a

{

}, (x₁, x₂, ..., x_k)

^k และ

ถ้า

(q, a, x₁, x₂, ..., x_k) = (q', y₁, y₂, ..., y_k, D, D₁, D₂, ..., D_k) แล้ว D

L และ D_i

L สำหรับแต่ละ i

{1, 2, ..., k} ที่ x_i = Z₀

หมายเหตุ

เราถือว่าเครื่องทัวริง k-แถบ ประกอบด้วยแถบทั้งหมด k+1 แถบ (นับแถบบันทึกข้อมูลรับเข้าเพิ่มอีกหนึ่งแถบ และที่เหลือเป็นแถบสำหรับหน่วยความจำอีก k แถบ) โดยแถบหน่วยความจำ k แถบเป็นแถบที่มีปลายเปิดทางเดียว
หัวอ่านของแถบบันทึกรับเข้าเคลื่อนขวาหรืออยู่ที่เดิมเท่านั้น (จึงไม่จำเป็นต้องมีสัญลักษณ์พิเศษ Z₀)
หัวอ่านของแถบสำหรับหน่วยความจำสามารถเคลื่อนซ้าย ขวาหรืออยู่ที่เดิมก็ได้ ดังนั้นจึงต้องมีสัญลักษณ์พิเศษ Z₀ เพื่อบอกตำแหน่งซ้ายสุดของแต่ละแถบ
หัวอ่านแต่ละแถบเคลื่อนที่ได้อย่างเป็นอิสระไม่ขึ้นต่อกัน
ในกรณีที่ไม่ได้ระบุ k เราเรียกรวมๆ ว่า เครื่องทัวริงหลายแถบ (multitape Turing Machine)
ในกรณีที่เราต้องการให้เครื่องทัวริงสามารถเขียนข้อมูลออก เราเพิ่มเซตของข้อมูลออกทั้งหมด และฟังก์ชันของข้อมูลออกดังนี้
เครื่องทัวริง k-แถบที่มีข้อมูลออก (k-tape Turing machine with output) แต่ละเครื่องประกอบด้วย Q, , , , q₀, Z₀, F เหมือนในบทนิยามของเครื่องทัวริง k-แถบ และให้ O เป็นเซตของสัญลักษณ์ข้อมูลออก และ เป็นฟังก์ชันข้อมูลออก ที่นิยามโดย
:_partial Q × ( {}) × ^k O × {R, S}

บทนิยาม แผนภาพการผ่าน (transition diagram) ของเครื่องทัวริง k-แถบ (Q,

, q₀, Z₀, F) คือกราฟเทียมระบุทิศทางที่มี Q เป็นเซตของจุดยอดทั้งหมด มีลูกศรชี้เข้าที่จุดยอด q₀ จุดยอดทุกจุดใน F มีวงกลมล้อมรอบสองวง และถ้า

(q, a, x₁, x₂, ..., x_k) = (p, y₁, y₂, ..., y_k, D, D₁, D₂, ..., D_k) แล้ว จะต้องมีอาร์กเชื่อมจากจุดยอด q ไปยังจุดยอด p โดยมี

(a, x₁, x₂, ..., x_k), (y₁, y₂, ..., y_k, D, D₁, D₂, ..., D_k) เขียนกำกับ

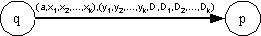
ในกรณีที่เครื่องทัวริงมีข้อมูลออก และถ้า

(q, a, x₁, x₂, ..., x_k) = (o, D') แล้ว เราจะเติม /(o, D') ต่อท้ายคือ

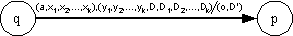
บทนิยาม เรากล่าวว่า c เป็น โครงแบบ (configuration) หนึ่งของเครื่องทัวริง k-แถบ M ก็ต่อเมื่อ

c = (q, x

iy,

₁

A₁

₁,

₂

A₂

₂, ...,

A_k

_k)

โดยที่ q

Q, x

^*, i

{

}, y

^* และ

^*, A_j

^* สำหรับทุก j = 1, 2, ..., k ซึ่งหมายถึง ขณะนั้นเครื่องทัวริง M อยู่ในสถานะ q สายอักขระที่ปรากฎบนแถบบันทึกรับเข้าคือ xiy โดยมีหัวอ่านชี้อยู่ที่ i และสำหรับแต่ละ j

{1, 2, ..., k} สายอักขระที่ปรากฎบนแถบหน่วยความจำแถบที่ j คือ

_jA_jB_j โดยมีหัวอ่านชี้อยู่ที่ A_j ดังรูป

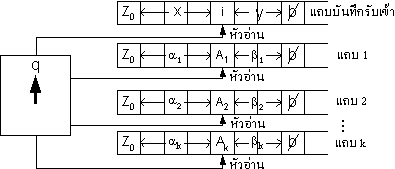
เราเรียก c ว่าเป็น โครงแบบเริ่มต้น (initial configuration) ก็ต่อเมื่อ q = q₀, x =

, i

{

₀ =

₁ = ... =

_k =

, A₁ = A₂ = ... = A_k = Z₀ และ

₁ =

₂ = ... =

_k =

โดยทั่วไปเราจะใช้สัญลักษณ์ c₀ แทนโครงแบบเริ่มต้น ดังนั้น

c₀ = (q₀,

iy,

Z₀,

Z₀, ...,

Z₀)

เรากล่าวว่า c เป็น โครงแบบหยุด (halting configuration) ก็ต่อเมื่อ q

F หรือ

(q, i, A₁, A₂, ..., A_k) ไม่มีค่า
สำหรับเครื่องทัวริงที่มีข้อมูลออก ถ้าบนแถบข้อมูลออกปรากฎสายอักขระ uo โดยมีหัวอ่านชี้ที่ o แล้ว เรานิยามโครงแบบโดยเพิ่ม u

o เข้าไปในตอนท้ายของโครงแบบ เขียนได้เป็น

c = (q, x

iy,

₁

A₁

₁,

₂

A₂

₁, ...,

A_k

_k, u

และโครงแบบเริ่มต้นคือ

c₀ = (q₀,

iy,

Z₀,

Z₀, ...,

Z₀,

)

ส่วนโครงแบบหยุดมีนิยามเหมือนเดิม
บทนิยาม

ให้ c = (q, x

iy,

₁

A₁

₁,

₂

A₂

₂, ...,

A_k

_k) และ

c' = (q', x'

i'y',

₁'

A₁'

₁',

₂'

A₂'

₂', ...,

_k'

A_k'

_k') เป็นโครงแบบของเครื่องทัวริง k แถบ M เครื่องหนึ่ง

ถ้า

(q, i, A₁, A₂, ..., A_k) = (p, y₁, y₂, ..., y_k, D, D₁, D₂, ..., D_k) แล้ว เรากล่าวว่า c' เป็น โครงแบบถัดจาก c (เขียนแทนด้วย c

c') ก็ต่อเมื่อ

p = q'
ข้อใดข้อหนึ่งในสองข้อนี้ต้องเป็นจริง
2.1 ถ้า D = R แล้ว x' = xi และ y = i'y'
2.2 ถ้า D = S แล้ว x = x', i = i' และ y = y'
สำหรับแต่ละ j {1, 2, ..., k} ข้อใดข้อหนึ่งในสามข้อนี้ต้องเป็นจริง
3.1 ถ้า D_j = R แล้ว _j' = _jy_j, _j = A_j' _j'
3.2 ถ้า D_j = L แล้ว _j = _j'A_j' และ _j' = y_j _j
3.3 ถ้า D_j = S แล้ว _j = _j', A_j' = y_j และ _j = _j'

เรากล่าวว่า c' เป็น โครงแบบที่ได้มาจาก c (เขียนแทนด้วย c

c') ก็ต่อเมื่อ c = c' หรือมีโครงแบบ c₁, c₂, ..., c_n ที่ c = c₁, c' = c_n และ c₁

c₂, c₂

c₃, ..., c_n-1

c_n

สำหรับเครื่องทัวริงที่มีข้อมูลออก ถ้า c = (q, x

iy,

₁

A₁

₁,

₂

A₂

₂, ...,

A_k

_k, u

o) และ

c' = (q', x'

i'y',

₁'

A₁'

₁',

₂'

A₂'

₂', ...,

_k'

A_k'

_k', , u'

o')

ต่างก็เป็นโครงแบบของเครื่องนี้ และถ้า

ถ้า

(q, i, A₁, A₂, ..., A_k) = (p, y₁, y₂, ..., y_k, D, D₁, D₂, ..., D_k) และ

(q, i, A₁, A₂, ..., A_k) = (v, N)

แล้ว นิยามของ c

c' จะเหมือนที่กล่าวข้างต้น กับเงื่อนไขเพิ่มเติมคือ

ถ้า N = R แล้ว u' = uv และ o' =
ถ้า N = S แล้ว u' = u และ o' = v

สำหรับนิยาม c

c' เหมือนกับข้างต้น
ตัวอย่างที่ 5 จงเขียนแผนภาพการผ่านของเครื่องทัวริงหลายแถบที่ยอมรับ L เมื่อ L = { w

{0,1}^* | n(0, w)

n(1, w) }
นอกจากนี้เรายังสามารถสร้างเครื่องทัวริงที่คำนวณค่าของฟังก์ชัน แล้วแสดงผลลัพธ์บนแถบข้อมูลออก ดังนี้
ตัวอย่างที่ 6 จงเขียนแผนภาพการผ่านของเครื่องทัวริงที่คำนวณค่าของฟังก์ชัน f :

ที่นิยามโดย f(n) = n+1 ทุก n

เมื่อกำหนดว่า n เขียนแทนด้วย

สายอักขระของ 1
เลขฐานสอง

หมายเหตุ

เรามักกำหนดให้เครื่องทัวริงที่คำนวณค่าฟังก์ชันมีแถบบันทึกรับเข้า และแถบข้อมูลออก โดยที่ขณะเริ่มต้นบนแถบรับข้อมูลเข้าจะมี สายอักขระที่แทนสมาชิกในโดเมนของฟังก์ชัน และเมื่อจบการทำงาน บนแถบช้อมูลออกจะปรากฎสายอักขระที่แทนค่าของฟังก์ชันที่จุดนั้น
เนื่องจากจำนวนฟังก์ชันที่ต่างกันทั้งหมดจาก ไปยัง มีจำนวนอนันต์แบบนับไม่ได้ แต่จำนวนเครื่องทัวริงที่คำนวณค่าของฟังก์ชันจากเซตดังกล่าวมีจำนวนอนันต์แบบนับได้ ดังนั้นจะมีฟังก์ชันบางชนิดซึ่งไม่มีเครื่องทัวริงที่คำนวณค่าของฟังก์ชันนั้นได้
ฟังก์ชันที่มีโดเมนเป็นสับเซตของ ^k และพิสัยเป็นสับเซตของ ที่เราสามารถสร้างเครื่องทัวริงที่คำนวณค่าของฟังก์ชันนั้นได้ มีชื่อเรียกว่า ฟังก์ชันทัวริง-คำนวณได้ (Turing-computable function) ซึ่งกลุ่มของฟังก์ชันนี้จะเป็นกลุ่มเดียวกับกลุ่มของฟังก์ชันรีเคอร์ซีฟ (recursive function)

ตัวอย่างที่ 7 จงสร้างเครื่องทัวริงที่คำนวณค่าของฟังก์ชันการบวกจำนวนนับสองจำนวน การหักออกของจำนวนนับสองจำนวน การคูณของจำนวนนับสองจำนวน
บทนิยาม เครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียวเชิงไม่กำหนด (Nondeterministic one-way infinite single tape Turing machine) เรียกสั้นๆ ว่า เอ็นทีเอ็ม (NTM) แต่ละเครื่องเป็นเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียวที่มีฟังก์ชันการผ่าน

สอดคล้องเงื่อนไขดังนี้

:_partialQ ×

เซตของสับเซตจำกัดทั้งหมดของ Q ×

× {R, L, S} โดยที่

(q, a) ไม่มีค่า ทุก q

F, a

ถ้า (p, X, D)

(q, Z₀) แล้ว D

โครงแบบของเอ็นทีเอ็ม เขียนแทนด้วย (q,

) เช่นเดียวกับนิยามของเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียว และถ้า c = (q,

) และ c' = (q',

) เป็นโครงแบบของเอ็นทีเอ็ม แล้วจะกล่าวว่า c' เป็นโครงแบบถัดจาก c (เขียนแทนด้วย c

c') ก็ต่อเมื่อ ข้อใดข้อหนึ่งในสามข้อต่อไปนี้ต้องเป็นจริง

(q', X, R) (q, i), ' = X และ = i'
(q', X, L) (q, i), = 'i' และ ' = X
(q', X, S) (q, i), i' = X, = และ = '

และเรากล่าวว่า c' เป็นโครงแบบที่ได้มาจาก c (เขียนแทนด้วย c

c') ก็ต่อเมื่อ c = c' หรือมีโครงแบบ c₁, c₂, ..., c_n ที่ c = c₁, c' = c_n และ c₁

c₂, c₂

c₃, ..., c_n-1

c_n
แผนภาพการผ่าน (Transition diagram) ของเอ็นทีเอ็ม จะเหมือนกับของเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียว สำหรับนิยามของเครื่องทัวริงเชิงไม่กำหนดอื่น ๆ ก็นิยามได้ในทำนองเดียวกัน
ตัวอย่างที่ 8 ให้ M = (Q,

, q₀, Z₀, F) เป็นเอ็นทีเอ็มที่มี Q = {q₀, q₁, q₂},

= {0, 1},

= {0, 1,

, X, Y}, F = {q₂} และ

นิยามดังนี้

	Z₀	0	1	Y
q₀	{(q₀, Z₀, R)}	{(q₁, X, R)}	{(q₀, 1, R), (q₁, Y, R)}	{(q₀, Y, R)}
q₁		{(q₀, 0, L)}	{(q₂, Y, L)}
q₂

จงตรวจสอบว่า M ยอมรับสายอักขระ 101 และ 100 หรือไม่

เครื่องทัวริงครอบจักรวาล (Universal Turing Machines)
เครื่องทัวริงที่ได้พิจารณา เปรียบเสมือนโปรแกรมแต่ละโปรแกรมที่สร้างเพื่อแก้ปัญหาเฉพาะอย่าง แต่โดยหลักการทำงานของ คอมพิวเตอร์ที่แท้จริงแล้ว ต้องสามารถทำงานได้หลายหลากขึ้นอยู่กับโปรแกรมที่ถูกเขียน เราจะศึกษาการสร้างเครื่องทัวริงที่จำลองการทำงานของ เครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียวเชิงกำหนดทุกเครื่องภายใต้สัญลักษณ์แบบเดียวกัน เพื่อความสะดวกเราจะกำหนด = {0, 1, , Z₀} เครื่องนี้เราจะให้ชื่อว่า เครื่องทัวริงครอบจักรวาล (Universal Turing Machines) หรือเรียกสั้น ๆ ว่า ยูทีเอ็ม (UTM)
สำหรับสัญลักษณ์ของสายอักขระรับเข้า เรากำหนดให้ใช้ได้เฉพาะ 0 หรือ 1 เท่านั้น ดังนั้นเราต้องมีการกำหนดรหัสให้กับเครื่องทัวริง ต่อไปเราจะนิยามการกำหนดรหัสที่ใช้กับเครื่องทัวริง
บทนิยาม ให้ M = (Q, , , , q₀, Z₀, F) เป็นเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียวเชิงกำหนดใด ๆ ที่มี = {0, 1, , Z₀}, Q = {q₁, q₂, ..., q_m} โดยที่ q₁ เป็นสถานะเริ่มต้น และ F = {q₂}

เราแทนสัญลักษณ์ที่ปรากฎบนแถบด้วย X₁, X₂, X₃, X₄ สำหรับ 0, 1, , Z₀ ตามลำดับ
เราแทนการเลื่อนหัวอ่านด้วย D₁, D₂, D₃ สำหรับ R, L และ S ตามลำดับ
และสำหรับแต่ละ i และ r {1, 2, ..., m}, j และ n {1, 2, 3, 4}, k {1, 2, 3},
เราแทน (q_i, X_j) = (q_r, X_n, D_k) ด้วยรหัส (code):
00...i ตัว ...0100...j ตัว...0100...r ตัว ...0100...n ตัว...0100...k ตัว...0

และแทนรหัสของเครื่องทัวริง M ด้วยรหัสของเครื่อง (Turing code)

111code₁11code₂11...11code_t111

เมื่อ code₁, code₂, ..., code_t เป็นรหัสของค่า

ทั้งหมด ของเครื่องทัวริงนี้
เราใช้สัญลักษณ์ <M> แทนรหัสของเครื่องทัวริง และถ้า w เป็นสายอักขระนำเข้าของ M เราจะแทนสัญลักษณ์ <M,w> หมายถึง 111code₁11code₂11...11code_t111w
ตัวอย่างที่ 9 ให้ M = ({q₁, q₂, q₃}, {0,1}, {0, 1,

, Z₀},

, q₁, Z₀, {q₂}) เป็นเครื่องทัวริงแถบเดี่ยวปลายเปิดทางเดียวเชิงกำหนดที่มี

นิยามดังนี้

(q₁, Z₀) = (q₁, Z₀, R),

(q₁, 0) = (q₁, 0, L),

(q₁, 1) = (q₃, 0, R),

(q₃, 0) = (q₁, 1, R),

(q₃, 1) = (q₂, 0, R),

(q₃,

) = (q₃, 1, L)

จงเขียนรหัสของเครื่องทัวริงนี้
ยูทีเอ็ม เปรียบได้กับเครื่องคอมพิวเตอร์ที่เราใช้งานอยู่ในปัจจุบัน และเครื่องทัวริงแต่ละเครื่องที่ถูกเข้ารหัสในแถบข้อมูลนำเข้าที่ยูทีเอ็มทำการจำลองเปรียบได้กับโปรแกรมต่าง ๆ ที่เครื่องคอมพิวเตอร์ใช้งานอยู่ เราจะใช้สัญลักษณ์ L_u แทนภาษาที่ยูทีเอ็มยอมรับ นั้นคือ

L_u = {<M, w> | M เป็นเครื่องทัวริง, w

{0, 1}^* และ M ยอมรับ w}

{0, 1}^*

Home | Previous | Next