Lecture 1:Introduction
Written byKrung Sinapiromsaran
July 2557
Outline
- Course plan
- Course definition for an algorithm
- Different between instructions, algorithms, processes
- Expressing algorithm
- Problem specification
- Algorithm Correctness
- Loop invariant
- Counter examples
- Reason for the analysis of an algorithm
Objective
- Understand terms and methodologies in Computer Science
- Know the origin of the word “Algorithm” and its informal definition
- Differentiate between step-by-step instructions / algorithms / processes
- Identify the specification of a problem
- Prove the correctness and give counter examples
- Give reason for the analysis of an algorithm
Three main components of this course
- Mathematical tools for analyzing algorithm
- Study of common algorithms and data structures
- Study of algorithm design strategies by examples
Course Philosophy
Aside from
- Mathematical tools for analyzing algorithm
- Study of common algorithms and data structures
- Study of algorithm design strategies by examples
You will need to learn using
- Neutral language for studying algorithms -- English/pseudocode
- Standard algorithms (Learn by examples)
- Group effort (Learn in team)
Course text book
 T.H. Cormen et al. Introduction to Algorithms. MIT Press, 2001.
T.H. Cormen et al. Introduction to Algorithms. MIT Press, 2001.
A lot of theorems and examples
Contains a lot of good references
Very useful for Computer Scientists
Need to have one (paper back or electronics)
References
 K. Mehlhorn and P. Sanders. Algorithms and Data Structures: The Basic Toolbox. Springer, 2008.
K. Mehlhorn and P. Sanders. Algorithms and Data Structures: The Basic Toolbox. Springer, 2008.
B.R. Preiss. Data Structures and Algorithms with Object-oriented Design Patterns in Java. Wiley, 1999. (+ other Java-specific texts)
R. Sedgewick. Algorithms. Addison Wesley, 1988.
S.S. Skiena. The Algorithm Design Manual. Springer, 2008.
References
 D.E. Knuth. The Art of Computer Programming. Addison Wesley, 1997. (In 3 volumes)
D.E. Knuth. The Art of Computer Programming. Addison Wesley, 1997. (In 3 volumes)
“If you think you’re a really good programmer, read Knuth’s Art of Computer Programming. You should definitely send me a resume if you can read the whole thing.”
Bill Gates
What is an algorithm?
 Muhammad ibn Mūsā al-Khwārizmī
Muhammad ibn Mūsā al-Khwārizmī
“algorism” referred to rules of performing arithmetic using Arabic numerals
Evolved into “algorithm” and came to mean a definite procedure for solving a problem or performing a task
“the idea behind any reasonable computer program”
Something like a recipe, process, method, technique, procedure, routine etc
What is an algorithm?
No formal definition has been accepted for all branches of Computer Science
- Finiteness: Must terminate after a finite number of steps.
- Definiteness: Each step must be precisely defined (rigourous, unambiguous). Programming languages are designed for specifying algorithms – every statement has a definite meaning.
- Input: Zero or more inputs.
Q: Are there any useful algorithms with no inputs? - Output: One or more outputs.
Q: Are there any useful algorithms with no outputs? - Effectiveness: Operations must be sufficiently basic that they can be done exactly and in a finite length of time, i.e. computable or do-able.
Valid algorithm?
According to our criteria, is the following statements valid algorithm?
Valid algorithm?
According to our criteria, is the following statements valid algorithm?
- Not valid (definiteness): “pinch of salt” “beat lightly” “mix well” “even overnight”
- All ambiguous
- As cooks, we can interpret approximately what is meant, but not precise enough for a computer to understand
Valid algorithm?
According to our criteria, is the following statements valid algorithm?
Valid algorithm?
According to our criteria, is the following statements valid algorithm?
- Not valid (Efficient): $10^{43}$ possible game states -- although finite, not realistic to evaluate all
- If we can evaluate 1 million states per second, we will need $3.2 \times 10^{29}$ years!
- Earth is about $4.5 \times 10^9$ years old
Valid algorithm?
According to our criteria, is the following statements valid algorithm?
Valid algorithm?
According to our criteria, is the following statements valid algorithm?
- Valid
- This is our first algorithm
- One of the oldest known algorithms (300 BC) described by Euclid (in a slightly different form)
Implement using Python
Valid algorithm?
According to our criteria, is the following statements valid algorithm?
Valid algorithm?
According to our criteria, is the following statements valid algorithm?
- Not valid (effectiveness)
- No such function $f(n)$ is known
- Until someone finds such a function, 1 is not an effective operation
Practical algorithm
In practice we want algorithms that are:
- Correct
- Efficient
- Easy to implement
Specification
- An algorithm is an implementation of a solution to a problem
- We need a way to specify a problem so we can design algorithms to solve it.
- A computer program is a translation of an algorithm into a particular programming language (also an implementation)
- Checking that an implementation correctly executes an algorithm is the realms of software engineering and formal methods
- We are interested in the design and analysis of algorithms
- We don’t care what language it is subsequently implemented in
- But we do need a language to express algorithms
Q: Why don’t we always use English? Why don’t we program computers in English?
Expressing Algorithm
- English
- Pseudocode
- A programming language
Expressing Algorithm
We will use a mixture of English and pseudocode.
- Pseudocode represents a good balance between precision and readability
- Should be straightforward to translate to any programming language.
- It’s intuitive - shouldn’t need to learn it.
Pseudocode of GCD
The algorithm for finding the greatest common divisor given above can be expressed in pseudocode as follows:
Python code of GCD
Specification and correctness
As algorists, we need tools to:
- Specify a problem so we can design algorithms to solve it
- Distinguish correct algorithms from incorrect ones
- Compare algorithms and choose the “best” one
Problem Specification
A very common (and useful) informal way to specify a problem is to list its inputs and outputs:
Sorting:
Input:A sequence of $n$ numbers; $a_1, a_2, ..., a_n$
Output:A permutation, $i_1, i_2, ..., i_n$ of the input sequence such that
\[ a_{i_1} \leq a_{i_2} \leq ... \leq a_{i_n} \]
Simple Specification
- Definition: A simple specification is a pair of predicates, one describing the starting states, the precondition, and one describing the associated final state, the postcondition.
- Factorial computational problem:
Precondition: $n \in \mathbb{N}$; Postcondition: $r$ = $n!$ - Sum from 1 to n computational problem:
Precondition: $n \in \mathbb{N}$; Postcondition: $r$ = $\displaystyle\sum_{i = 1}^{n} i$. - Preconditions and postconditions are like a contract between the caller and the algorithm:
- Algorithm: “If you ensure the precondition is satisfied, I’ll guarantee that the postcondition is satisfied upon termination”
- Caller: “Ok, and if I don’t ensure the precondition is satisfied I’ll make no assumptions about what your behaviour will be”
GCD Specification
- Let’s think up pre/postconditions for the greatest common divisor algorithm:
- Precondition: $m, n \in \mathbb{N} \& (m > 0) \mbox{ and } (n > 0)$
Postcondition: $(r|m)$ and $(r|n)$ amd $\forall i \in \mathbb{N}; (i|m) \mbox{ and } (i|n) \rightarrow i \leq r$.
Certifying GCD Algorithm
- Sometimes preconditions and postconditions can be easily checked
- Many programming languages support assertions – good practice to check pre/postconditions, example:
Certifying Algorithms
- This might seem a bit circular – isn’t checking the postcondition as hard as running the algorithm in the first place?
- In many situations checking assertions can be simplified by computing additional information – a certificate
- A certifying algorithm computes a certificate for the postcondition
- We will see examples of algorithms later where a certificate can be computed without affecting the efficiency of the algorithm
Loop invariant
- A loop invariant is a statement which is true before and after each loop iteration
- Used to help prove program correctness
- Helps to clarify purpose of iterative structure
- Loop variant ensures progress is made
Reasoning about correctness
- We need to know whether our algorithm will always work, i.e. produce the correct/optimal answer.
- Let’s look at an example:
Robot Tour Optimization
Robot arm must visit a set of contact points on a circuit board to solder each point Need to choose an order in which the contact points will be visited We want to minimise time taken, i.e. shortest path Shorter tour = faster production = cheaper to produce = more profit
Nearest neighbor heuristic
Input: A set $P$ of $n$ points
Output: The shortest cycle tour that visits each point
- Simple idea: nearest neighbor tour
- Use a heuristic – pick any starting point, then next move is always to nearest point
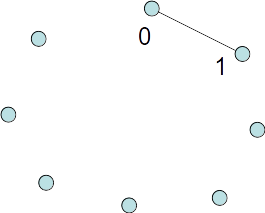
Tour with nearest neighbor heuristic
Tour example
Tour example
Tour example
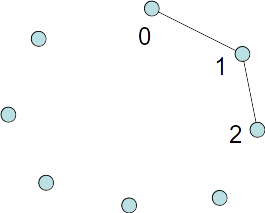
Tour example
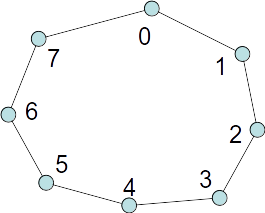
Look encouraging
Tour example
- Look encouraging
- Optimal for this instance!
- Q:Always optimal?
- Q:What is needed to prove incorrectness?
Counter tour example
An instance where nearest neighbor gives a suboptimal solution

Tour example

Counter tour example

Counter tour example

Counter tour example

Counter tour example

Counter tour example
A better (optimal) solution for the same instance:


- It can be easy to prove that an algorithm is not correct – just find a counter example (the simpler, the better)
- Counter example = instance of problem + optimal solution + demonstration that algorithm produces a less optimal solution
- Lack of a counter example doesn’t prove it works
- We will not study the formal methods to prove correctness of our algorithms
- Instead, we will informally convince ourselves that they work
Specification and correctness
As algorists, we need tools to:
- Specify a problem so we can design algorithms to solve it and strategies to design algorithms which satisfy specifications
- Distinguish correct algorithms from incorrect ones
- Check that the algorithm satisfies the problem specification
- Compare algorithms and choose the “best” one
- There may be many alternative algorithms that satisfy a specification
- We want the one that is “best” for our purposes
- Often, best = most efficient. Is this always the case?
- The subject of much of this course!
Analysis of algorithms
The theoretical study of computer program performance and resource usages.
- Is performance the most important measure of an algorithm?
- What’s more important than performance? correctness; security; user-friendliness; maintainability; robustness/reliability; functionality/features; simplicity; programmer time; modularity; extensibility
- Performance is the currency of computation
- We can use it to buy other things: functionality, user-friendliness etc.
Why study analysis of algorithms?
- Some algorithms experts are lousy programmers, but no good programmer can be bad at algorithms
- Algorithm design and analysis is the essence of what we do as computer scientists
- With more sophisticated software engineering systems, the demand for mundane programmers will diminish
- Soon all known algorithms will be available in libraries
Why study analysis of algorithms?
- Great thinkers will always be needed: “I can develop a new algorithm for you”
- “To be a good programmer you can either study programming for 10 years or take an algorithms course and study programming for 2 years”
- Making things faster is fun! Some people try to design faster cars, we try to design faster algorithms!
Conclusion
- What an algorithm is
- How to specify a problem
- How to show algorithm incorrectness by counter example
- Some justification for why algorithm analysis is important
Comments and Suggestions
- Assistant Professor Krung Sinapiromsaran
- Web: http://pioneer.netserv.chula.ac.th/~skrung
- Email: Krung.S@chula.ac.th
